Sketching Sampling and other Sublinear Algorithms Euclidean space

Sketching, Sampling and other Sublinear Algorithms: Euclidean space: dimension reduction and NNS Alex Andoni (MSR SVC)

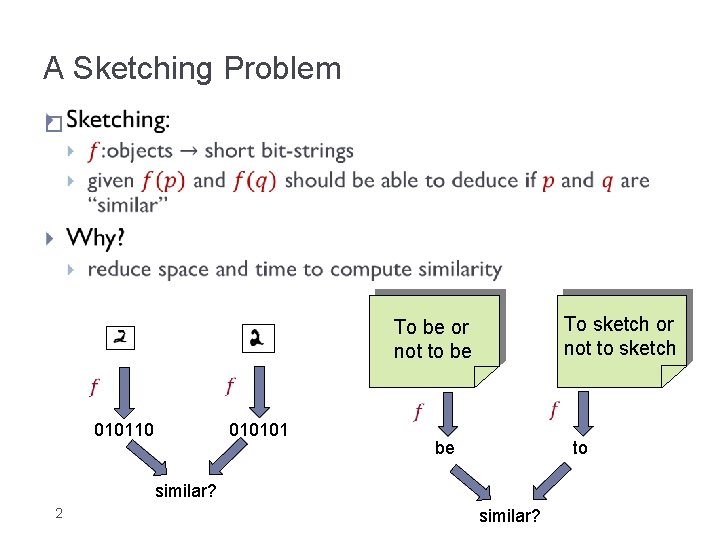
A Sketching Problem � To sketch or not to sketch To be or not to be 010110 010101 be to similar? 2 similar?

Sketch from LSH � 1 [Broder’ 97]: for Jaccard coefficient 3

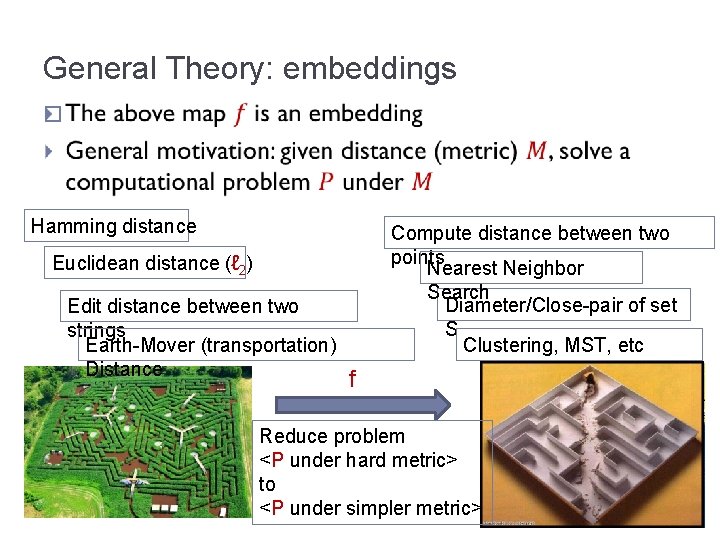
General Theory: embeddings � Hamming distance Compute distance between two points Nearest Neighbor Search Diameter/Close-pair of set S Clustering, MST, etc Euclidean distance (ℓ 2) Edit distance between two strings Earth-Mover (transportation) Distance f Reduce problem <P under hard metric> to <P under simpler metric>

Embeddings: landscape �

Dimension Reduction �

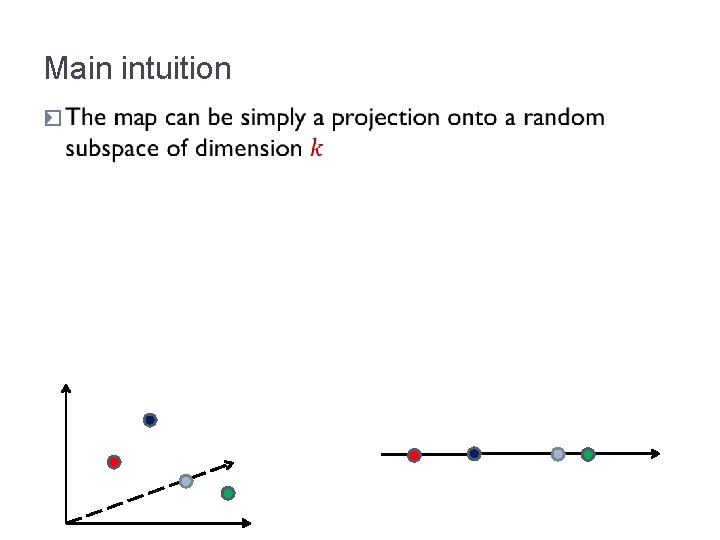
Main intuition �

1 D embedding �

1 D embedding � 2 2

Full Dimension Reduction �

Concentration �

Dimension Reduction: wrap-up �

NNS for Euclidean space [Datar-Immorlica-Indyk-Mirrokni’ 04] � 13

Near-Optimal LSH [A-Indyk’ 06] �Regular grid → grid of balls p � p can hit empty space, so take more such grids until p is in a ball �Need (too) many grids of balls � Start by projecting in dimension t �Analysis gives �Choice of reduced dimension t? 2 D � Tradeoff between � # hash tables, n , and � Time to hash, t. O(t) 2 � Total query time: dn 1/c +o(1) p Rt

Open question: � 2 c [Prob. needle of length 1 is not cut] ≥ [Prob needle of length c is not cut]

Time-Space Trade-offs space low query time Space Time Comment Reference [Ind’ 01, Pan’ 06] high [AI’ 06] [IM’ 98] medium [DIIM’ 04, AI’ 06] n 1+o(1/c 2) high ω(1) memory lookups [PTW’ 08, PTW’ 10] one hash table lookup! low [KOR’ 98, IM’ 98, Pan’ 06] no(1/ε 2) ω(1) memory lookups [AIP’ 06]

NNS beyond LSH � 17

Finale �