Size of giant component in Random Geometric Graphs

![Random Geometric Graph • n nodes uniformly distributed in S = [-½, ½]2 • Random Geometric Graph • n nodes uniformly distributed in S = [-½, ½]2 •](https://slidetodoc.com/presentation_image_h/181dee283468f8db3d12da0f622da2e7/image-2.jpg)









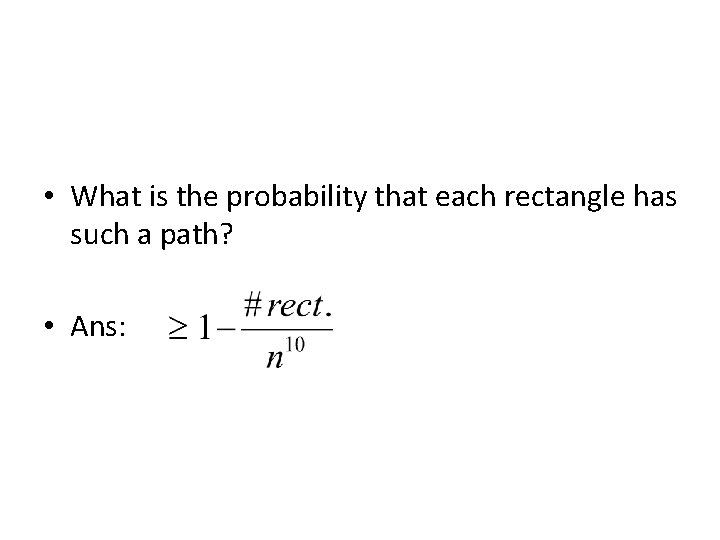
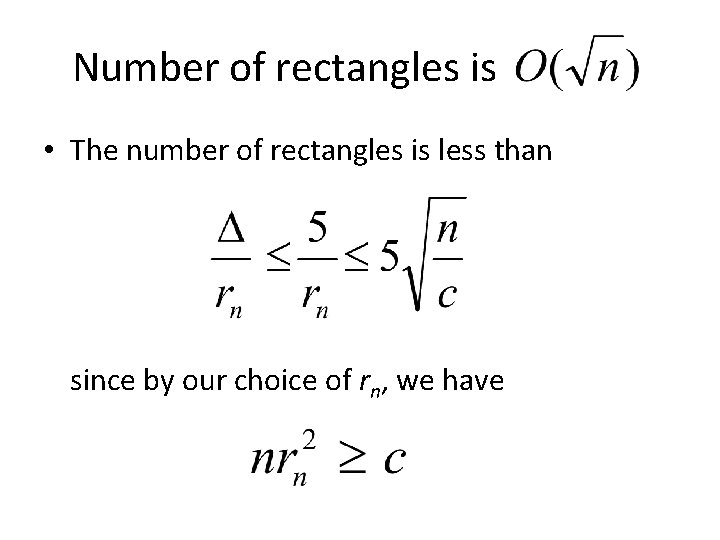













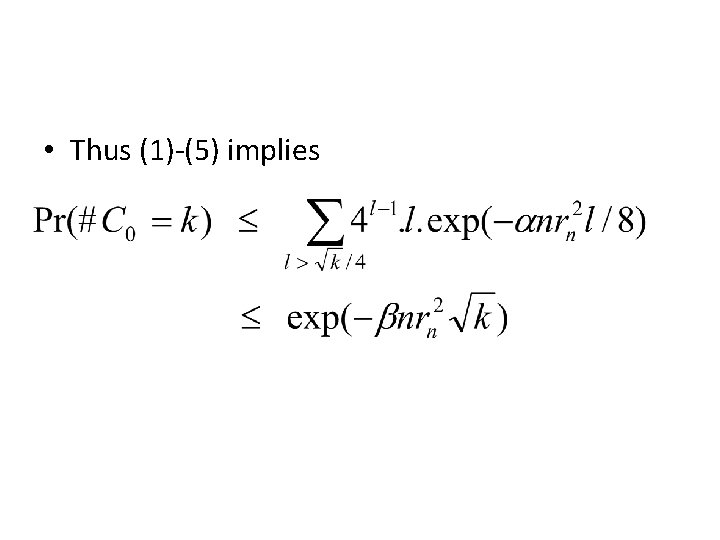






- Slides: 49

Size of giant component in Random Geometric Graphs -G. Ganesan Indian Statistical Institute, Delhi.
![Random Geometric Graph n nodes uniformly distributed in S ½ ½2 Random Geometric Graph • n nodes uniformly distributed in S = [-½, ½]2 •](https://slidetodoc.com/presentation_image_h/181dee283468f8db3d12da0f622da2e7/image-2.jpg)
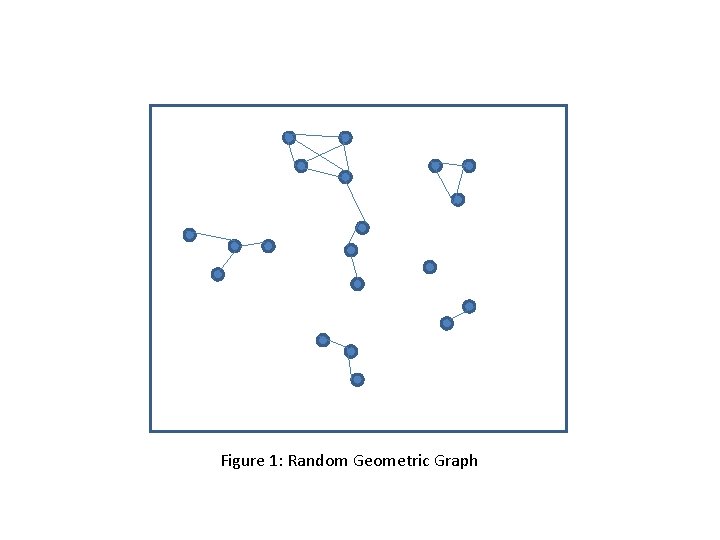
Random Geometric Graph • n nodes uniformly distributed in S = [-½, ½]2 • Two nodes u and v connected by an edge if d(u, v) < rn • Resulting graph random geometric graph (RGG)

Figure 1: Random Geometric Graph

Radius of Connectivity •

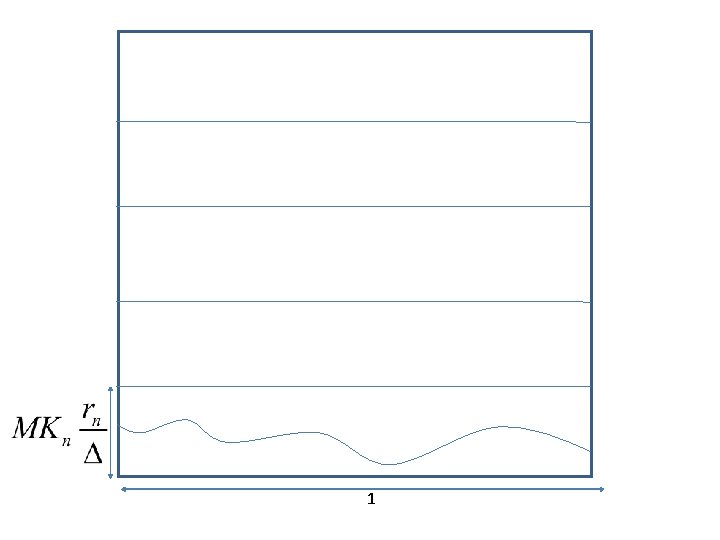
Giant Component Regime • Sparse, no Giant Comp. Intermediate, Dense, Has giant component fully connected rn

Intermediate range •

Theorem 1 (Ganesan, 2012) •

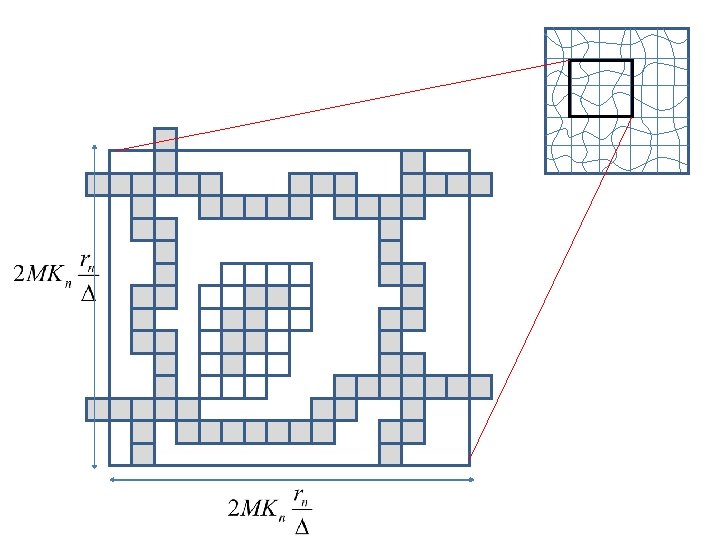
Proof Sketch of Theorem 1 • Divide S into small squares {Si}i each of size • Choose 4 < ∆ < 5 so that nodes in adjacent squares are joined by an edge. • Say that Si is occupied if it contains at least one node and vacant otherwise. S

S • Also, divide the unit square S into ``horizontal” rect. each of size where • Fix the bottom rectangle R R

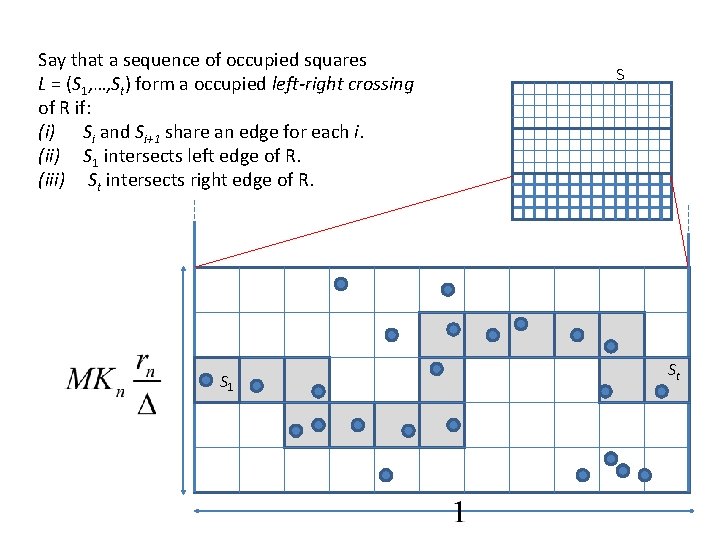
Say that a sequence of occupied squares L = (S 1, …, St) form a occupied left-right crossing of R if: (i) Si and Si+1 share an edge for each i. (ii) S 1 intersects left edge of R. (iii) St intersects right edge of R. S 1 S St

1

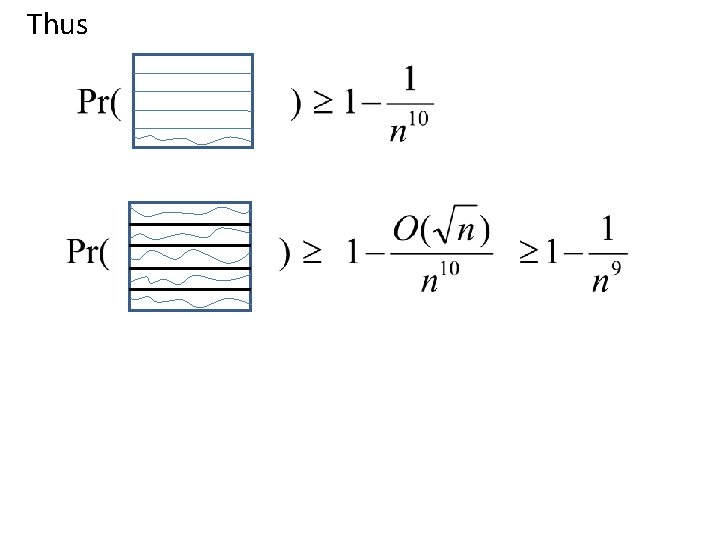
Probability of left-right crossing • Let LR(R) denote the event that R has an occupied left-right crossing… • Lemma (Ganesan, 2012): We have that for some positive constant δ.

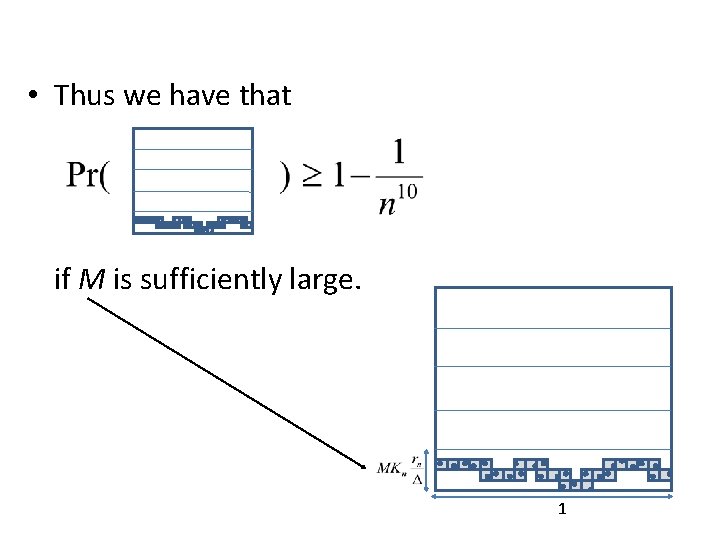
• Thus we have that if M is sufficiently large. 1

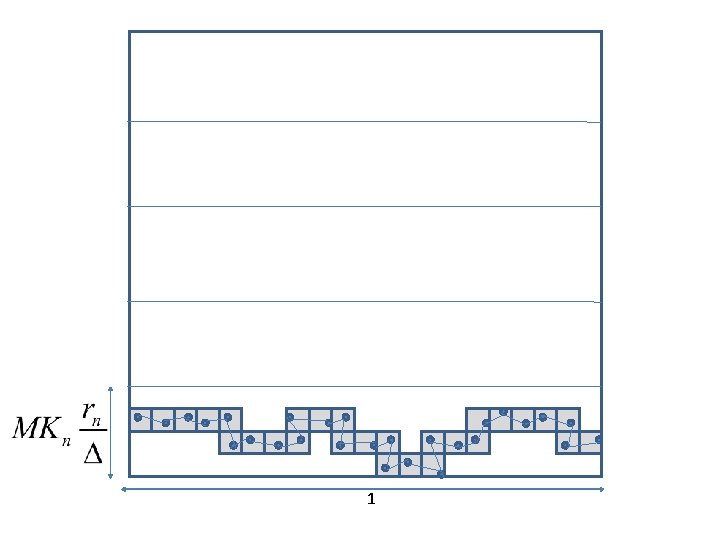
• What is the advantage of identifying occupied left-right crossings. . • Ans: We get a path of edges from left to right…

1

1

Thus
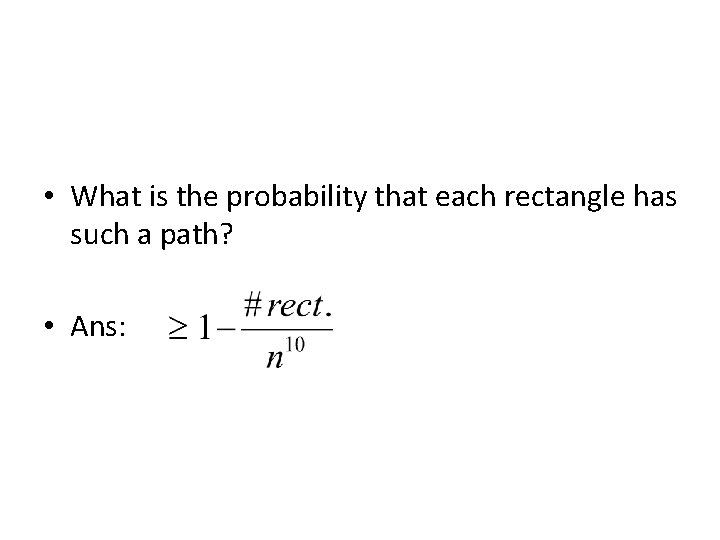
• What is the probability that each rectangle has such a path? • Ans:
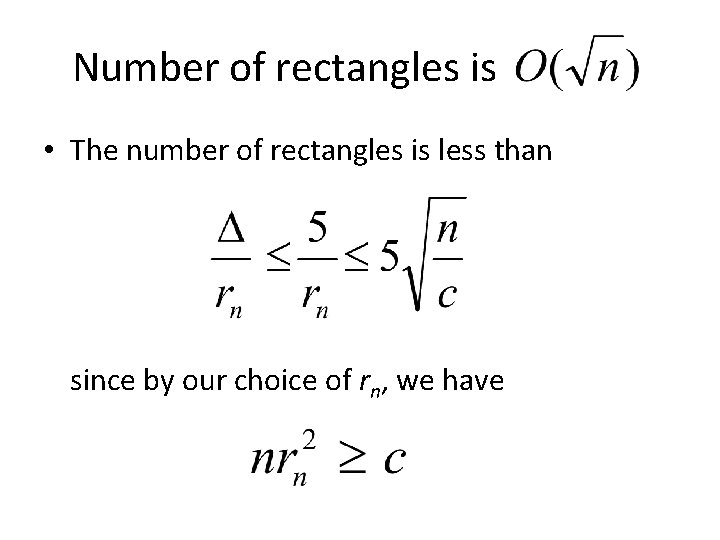
Number of rectangles is • The number of rectangles is less than since by our choice of rn, we have

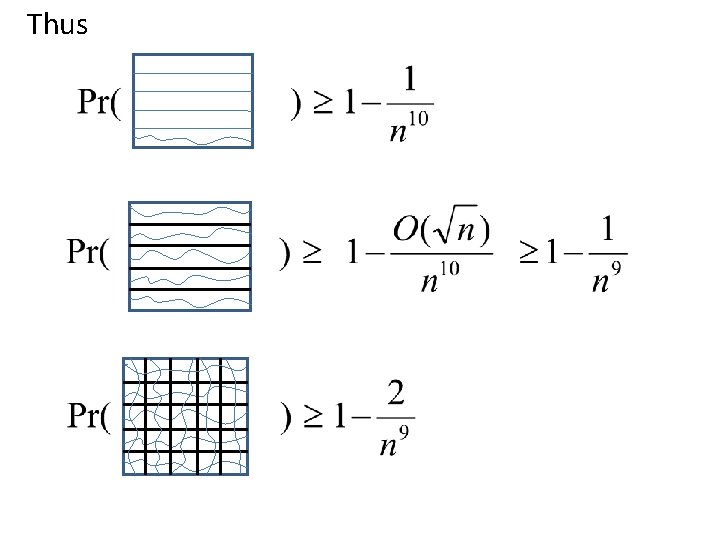
• Thus… • The event that each rectangle has an occupied left-right crossing occurs with prob. • And we then get a network of paths from left to right…

1

Thus

• Perform an analogous procedure vertically…

1

Thus

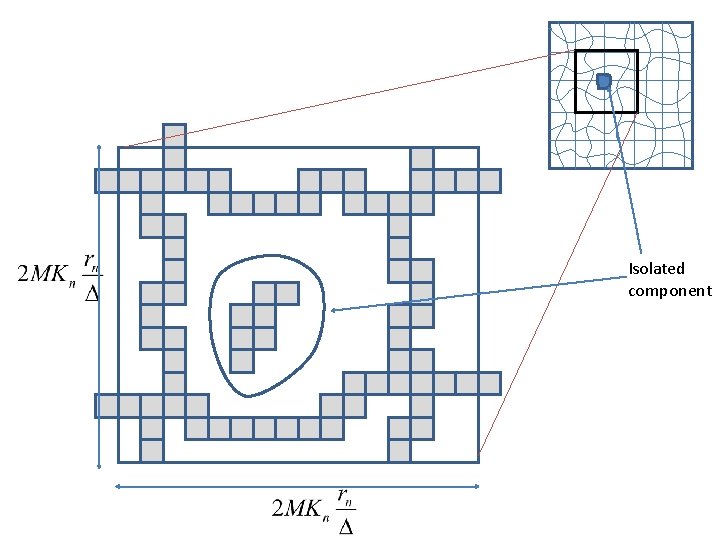
Why is this useful? • We have obtained a connected “backbone” of paths in G… • We have essentially “trapped” isolated components of G in boxes of size…

Isolated component

• So, we know that if backbone occurs… then all components not attached to backbone are “boxable” , i. e. , can be fitted in a box…

• Let X denote the sum of size of all components of G that are boxable… (1) for some positive constants • Recall that backbone occurs with prob. .

Thus Note: Whenever backbone occurs, X denotes total sum of sizes of components not attached to the backbone… Therefore

• We need to prove the estimate (1) regarding sum of sizes of boxable components… i. e. to prove that Recall: X sum of size of all components of G that are boxable

Proof of (1) • How to compute the size of a component that can be fitted in a size box? • Main idea…count the number of vacant squares attached to the component…


• Observation from figure… • “Boxable” components have a circuit of vacant squares attached to them… • For any square Si (proved using standard binomial estimates)

• We therefore cannot have large boxable components… • Because, such components have a lot of vacant squares ``attached” to them…

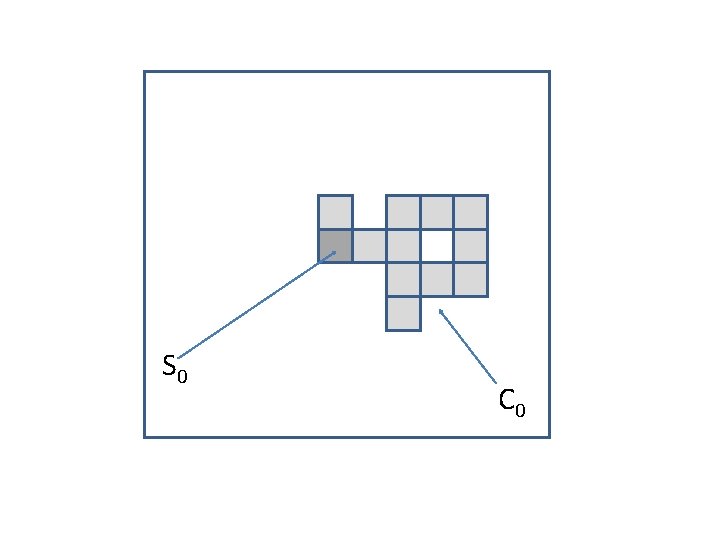
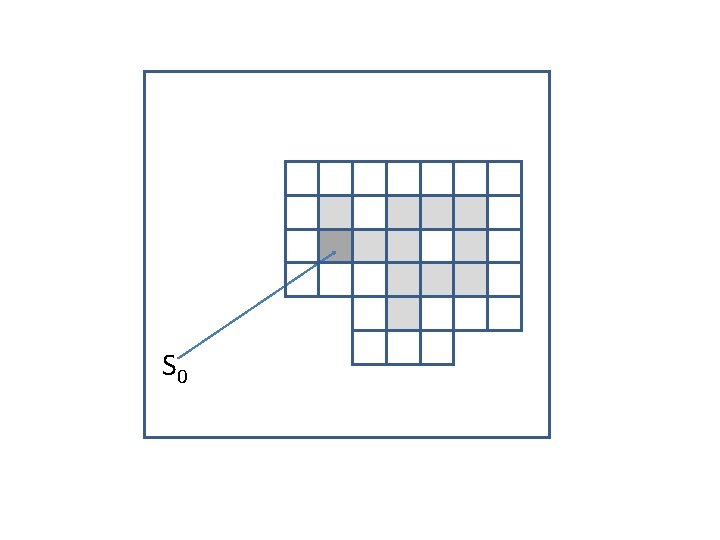
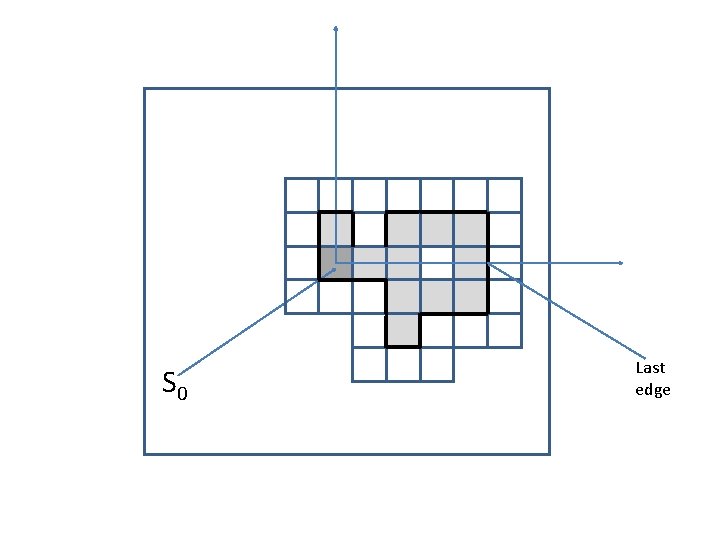
More precise computation • Let S 0 be the square containing the origin… • Define C 0 to be the maximal connected set of occupied squares containing S 0… • We say that C 0 is the cluster containing S 0…

S 0 C 0

S 0

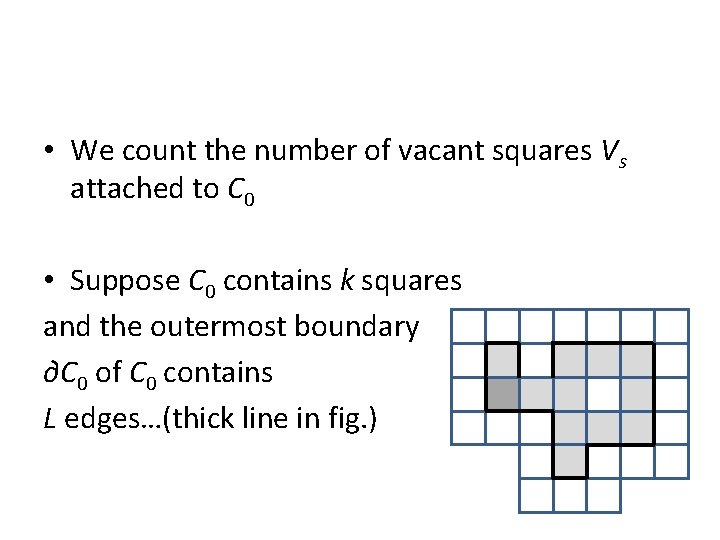
• We count the number of vacant squares Vs attached to C 0 • Suppose C 0 contains k squares and the outermost boundary ∂C 0 of C 0 contains L edges…(thick line in fig. )

The following hold: • (1) The number of distinct vacant squares attached to ∂C 0 is at least Vs > L/8… • (2) Since ∂C 0 contains k squares in its interior, we must have

• (3) Also, the ``last edge” of ∂C 0 can cut the X axis at at most L distinct points… • (4) And ∂C 0 has a self-avoiding path of L-1 steps. • (5) The number of choices of ∂C 0 is therefore at most L. 4 L-1

S 0 Last edge
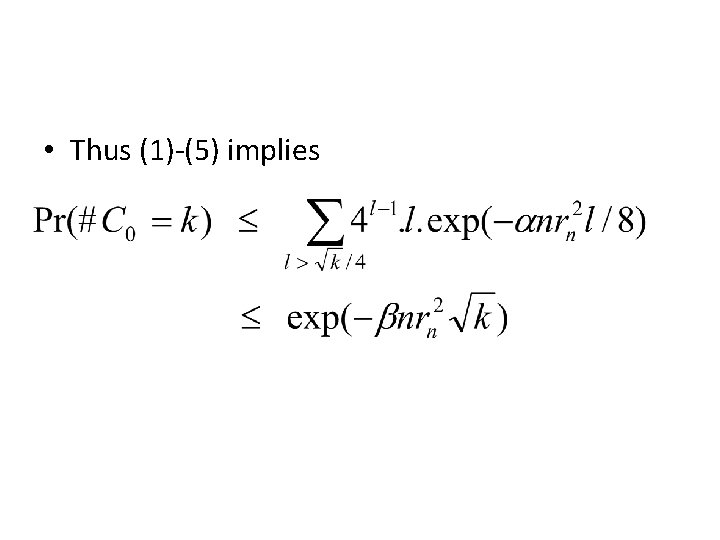
• Thus (1)-(5) implies

• Thus…. • And if N(C 0) denotes the number of nodes is C 0, we also have

• Recall C 0 is the occupied cluster containing S 0… • Define Ci for each square Si • Same conclusion holds…

• Use Markov’s inequality to get… for θ sufficiently small… • But is the sum of size of all boxable components… • And we are done…

Main summary of steps • (1) We constructed a backbone of paths with high prob. . … • (2) We deduced that each component not attached to the backbone is “boxable” • (3) We showed that the sum of sizes of all “boxable” components is less than with high prob…

References • M. Franceschetti, O. Dousse, D. N. C. Tse and P. Thiran. (2007). Closing Gap in the Capacity of Wireless Networks via Percolation Theory. IEEE Trans. Inform. Theory, 53, 1009– 1018. • G. Ganesan. (2012). Size of the giant component in a random geometric graph. Accepted for publ. Ann. Inst. Henri Poincare. • A. Gopalan, S. Banerjee, A. K. Das and S. Shakottai. (2011). Random Mobility and the Spread of Infection. Proc. IEEE Infocomm, pp. 999– 1007.

• P. Gupta and P. R. Kumar. (1998). Critical Power for Asymptotic Connectivity in Wireless Networks. Stoch. Proc. and Appl. , 2203– 2214. • M. Penrose. (2003). Random Geometric Graphs. Oxford.