Sisteme de programe pentru timp real Universitatea Politehnica

Sisteme de programe pentru timp real Universitatea “Politehnica” din Bucuresti 2007 -2008 Adina Magda Florea http: //turing. cs. pub. ro/sptr_08 si curs. cs. pub. ro

Curs Nr. 2 Criptologie si criptosisteme • • • Numere aleatoare Operatii aritmetice cu numere mari Criptologie – generalitati Criptosisteme conventionale Criptosisteme publice Standarde actuale 2

1. Numere aleatoare • Numar intreg/real aleator intr-un domeniu dat si cu o precizie fixata / Numar pseudoaleator • Generator de numere aleatoare - o multime de stari S, o functie f: S S si o stare initiala s 0 samanta. • Starile generatorului evolueaza dupa relatia: si=f(si-1), cu i =1, 2, . . . g: S (0, 1) • Perioada unui generator de numere aleatoare este cel mai mic intreg pozitiv p a. i. si+p=si , i > p 0 3

Sunt numere aleatoare? • Testul • N numere intregi in intervalul [ 0, r ), frecventa fiecarui numar din interval fiind fi ( i = 0, r-1 ) • Distributii uniforme (aceeasi probabilitate) 4

1. 1 Metoda congruent multiplicativa • f (si+1) = ( b*si + c ) mod m g ( si ) = si/m s 0 - samanta , b, c < m, pozitivi f(si) [ 0, m-1 ] int a [ Max ] a [ 0 ] = sam ; for ( i = 1; i <= N; i++ ) a [ i ] = ( a [ i-1 ] * b + 1 ) % m 5

1. 1 Metoda congruent multiplicativa • Cum se aleg m, s 0 si b ? • m trebuie sa fie mare = perioada maxima (aproape de limita cuvantului calculatorului); m poate fi prim • b trebuie sa fie prim relativ la m. • O alegere este: b sa se termine cu. . . x 21 si x sa fie par. • Cum calculez ? • Fiecare valoare este mai mica decat cel mai mare intreg, dar prima operatie a*b+1 duce la overflow • Cum se elimina overflow-ul? 6

Cum se elimina overflow-ul? • Reprezentare pe 32 de biti - intereseaza pentru rezultat numai ultimii 8 digiti. • Alegem a = 1234567 b = 31415821 • a si b se reprezinta ca doua polinoame in fct. de x. (a*b +1) mod m grad(p) N-1 grad(q) N-1 grad(p*q) 2 N-2 p = 104 * p 1 + p 0 q = 104 * q 1 + q 0 p * q = ( 104 *p 1 + p 0 ) ( 104 q 1 + q 0 ) = 108 * p 1 * q 1 + 104 * ( p 1 * q 0 + p 0 * q 1 ) + p 0 * q 0 7

Generare numere aleatoare #define m 10000 #define m 1 10000 #define b 31415821 108 * p 1 * q 1 + 104 * ( p 1 * q 0 + p 0 * q 1 ) + p 0 * q 0 long int a =1234567; long int mult( long int p , long int q ) { long int p 0, p 1, q 0, q 1; p 1 = p / m; p 0 = p % m 1; q 1 = q / m 1; q 0 = q % m 1; return ((p 0 * q 1 + p 1 * q 0) % m 1)*m 1 + p 0* q 0)% m ; } long int random( ) { a = ( mult( a, b ) + 1 ) % m ; return a; } // nr. aleatoare [0, m-1] // echiv rand() RAND_MAX=m-1 8

1. 2 Metoda congruent-aditiva • Registru de deplasare cu feed-back • Adunare • 1111 • 0111, 0001, 1000, . . . • Pt. n biti se pot obtine secvente de max. 2 n-1 numere distincte • n = 31 sunt bune pozitiile 0 si una din pozitiile 4, 7, 8, 14, 19, 25, 26 sau 29. 9

Metoda congruent-aditiva • Adunare b c • Considerand un sir de numere aleatoare a 0 …ak, se obtin numere aleatoare in continuare in [ 0, m-1 ], astfel • a [ k ] = ( a [ k-b] + a [ k-c ] ) % m (b<c) • min 2 c-1 numere distincte • Valori b = 31, c = 55 • a – coada circulara 10

2 Operatii aritmetice cu numere mari • Reprezentare • Intregul 0120200103110001200004012314 cu N = 28 digiti se reprezinta prin p(10) unde p este polinomul • Calcul eficient al inmultirii a doua polinoame p(x) si q(x) de grad N-1 • Produs de grad 2 N-2 cu 2 N-1 termeni • Produs calculat direct – N 2 inmultiri • Divide and conquer • N – par => 2 polinoame de grad N/2 11

Utilizare “Divide and conquer” p( x ) = p 0 + p 1 x +. . . + p. N-1 x. N-1 pi( x ) = p 0 + p 1 +. . . +p. N/2 -1 x. N/2 -1 ps( x ) = p. N/2 +. . . + p. N-1 x. N/2 -1 • Pentru a calcula p ( x ) * q ( x ) sunt necesare numai 3 inmultiri • Doua polinoame de grad N pot fi inmultite folosind inmultiri 12

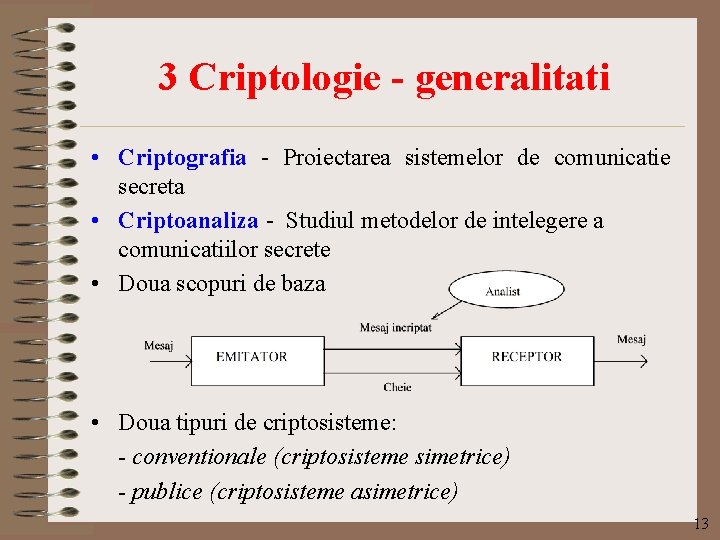
3 Criptologie - generalitati • Criptografia - Proiectarea sistemelor de comunicatie secreta • Criptoanaliza - Studiul metodelor de intelegere a comunicatiilor secrete • Doua scopuri de baza • Doua tipuri de criptosisteme: - conventionale (criptosisteme simetrice) - publice (criptosisteme asimetrice) 13

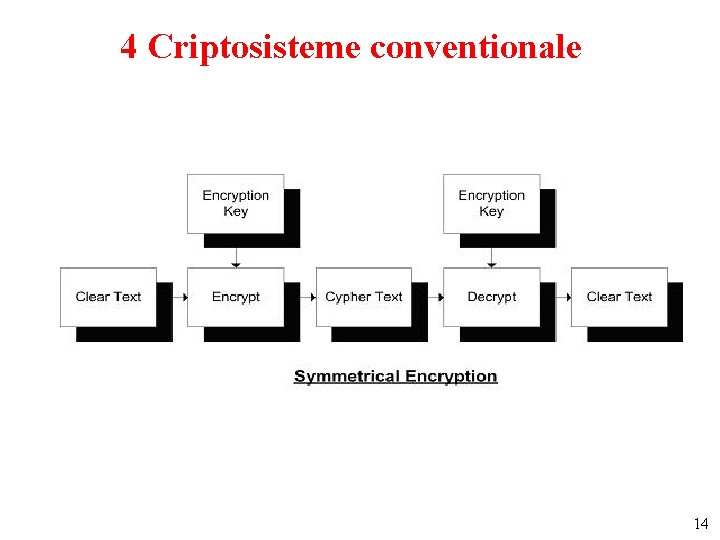
4 Criptosisteme conventionale 14

Criptosisteme conventionale Metode simple • Cifrul lui Cezar – a N-a litera din alfabet se inlocuieste cu litera (N+k) din alfabet, unde k este constant (Cezar lua k = 3) • Substitutie simpla - Matrice cu 26 linii si 2 coloane care defineste substitutia literelor • Cifrul Vigenere: se utilizeaza o cheie pentru a determina valorile lui k care trebuie adaugate fiecarei litere. Fie cheia c 1 c 2. . . cm. j 0 pentru fiecare litera li din mesaj executa li din mesaj are indexul p in alfabet j ( j+1 ) mod m alege cj din cheie fie k indexul lui cj in alfabet inlocuieste li cu litera din alfabet de index ( k + p ) sfarsit 15

Criptosisteme conventionale • • • Cifrul Vigenere se poate combina cu substitutia simpla Daca cheie mesaj Cifrul Vernam (one time pad) Masini de criptare/decriptare - primeste un numar de chei adevarate, numite criptovariabile, care sunt utilizate pentru a genera chei lungi Generarea pseudocheii din criptovariabile este asemanatoare cu metoda congruent aditiva (cu registru) de la numere aleatoare Pericol Dificultati ale sistemelor conventionale 16

5 Criptosisteme publice Idee: fiecare utilizator are o cheie publica P care poate fi cunoscuta de oricine si o cheie secreta S cunoscuta numai de el. • Mesaj M • E - cheia publica P a receptorului - C = P ( M ) • R - cheia secreta S - M = S ( C ) 17

Criptosisteme publice • • Conditii S ( P ( M ) ) = M pentru fiecare mesaj M Toate perechile ( S, P ) sa fie distincte Deducerea lui S din P sa fie la fel de dificila ca si decriptarea lui C Atat S cat si P sunt usor de calculat 18

6. Standarde actuale Conventionale • DES – Data Encryption Standard • AES – Advanced Encryption Standard Publice • RSA - Ron Rivest, Adi Shamir, and Leonard Adelman • DSA – Digital Signature Algorithm • DSS – Digital Signature Standard • NIST (National Institute of Standards and Technology, USA) lucreaza la Federal Public Key Infrastructure – va sustine semnaturile digitale

7 Criptosistemul public RSA • Cheia de incriptare P este o pereche de intregi ( N, p ) cu p public • Cheia de decriptare S este o pereche de intregi ( N, s ) unde s este secret. Aceste numere trebuie sa fie foarte mari, in mod tipic N 200 digiti iar p si s aproximativ 100 digiti Metoda de criptare/decriptare 1. Se imparte mesajul in k grupri de biti M 1…Mk 2. Se incripteaza mesajul astfel: C = P(M) = C 1…Ck unde Ci = (Mpi) mod N R 3. Receptorul decripteaza mesajul M = S(C) = M 1. . . Mk unde Mi = (Csi) mod N 20

Modul de alegere a p si s 1. Se genereaza trei numere aleatoare prime mari ( 100 digiti ) x, y, z. 2. Cel mai mare dintre acestea este ales ca valoare a lui s. 3. Fie celelalte doua numere x si y. 4. N = x * y 5. p se alege astfel incat p * s mod ( x-1 ) * ( y-1 ) = 1. Se poate demonstra ca, pt. aceste alegeri, Este sigur? 21

Cum se genereaza un nr. prim f. mare? Se genereaza un nr. aleator f. mare + se testeaza daca este prim Fie w numarul pentru care se testeaza daca este prim. 1. i 1, n 50 2. Determina a si m a. i. w=1+2 am , unde m este impar si a este cea mai mare putere a lui 2 care divide w-1. 3. Genereaza un numar aleator b ( 1, w ) 4. j 0, z bm mod w 5. daca (( j=0 ) si ( z=1 )) sau ( z=w-1 ) atunci executa pasul 9 6. daca ( j>0 ) si ( z=1 ) atunci executa pasul 8 22

Cum se genereaza un nr. prim f. mare? Iterat de n ori va raspunde incorect ca numarul este prim cu o probabilitate de cel mult 1/4 n j j+1 daca j<a atunci z z 2 mod w executa pasul 6 8. w nu este prim stop 9. daca i<n atunci i = i + 1; executa pasul 3 altfel w este probabil prim sfarsit 7. 23

Discutie criptosisteme publice • Toate abordarile se bazeaza pe calcule NP • Problema: daca se inlocuieste p (cu s asociat) cu p’ (si s’ asociat) • Managementul de chei implica – Genererarea cheilor – Cautarea cheilor – Distribuirea cheilor – Incredere in cheile publice • Cheile publice – certificate de cheie (digitale) • Cheia secreta – cheie incriptata cu o parola 24

Certificate digitale: verifica daca o cheie publica apartine unui individ Un certificat contine: • Un nume si cheia publica • Data de expirare • Numele autoritatii de certificare • Numar de serie • Semnatura digitala a autoritatii de certificare Receptorul verifica un certificat folosind cheia publica a autoritatii de certificare Se autentifica astfel semnaturile digitale mesajelor • Lungimea cheii 1024 bits. • 512 bits nesigur • 2048 , 4096 bits. • In practica, 512 -bit key. 25

8. Criptosisteme conventionale - DES • • • Criptare sir Criptare blocuri Simetrice – mai rapide Simetrice – fnct de incriptare – reversibila Criptare pe blocuri – p 1, p 2 -> p 2’, p 1 --- runda – p 2’= p 2 + f(p 1, cheie) • f - functie hash unidirectionala • Dim bloc: 64, 128 bits sau variabila • Dim cheie: 40, 56, 64, 80, 128, 192, 256 bits 26

Functie hash unidirectionala • F hash cu proprietati suplimentare – securitatea informatiei – fiind dat h – greu de aflat m al h = hash(m) – fiind dat m 1 - greu de gasit m 2<>m 1 ai hash(m 1)=hash(m 2) – greu de gasit m 1 si m 2 ai hash(m 1)=hash(m 2) • F hash – mesaj de lungime variabila intr-o iesire de lungime fixa • Imparte intrarea in 2 parti, fiecare se comprima cu o functie de compresie 27

DES – Data Encryption Standard • Data Encryption Standard (DES) adoptat ca standard in USA in 1977 (IBM – Lucifer) de FIPS (Federal Information Processing Standard of USA) • Foloseste o cheie de 56 -bits – insuficient • Varianta Triple-DES (TDES or 3 DES) – foloseste o cheie mai lunga • Advanced Encryption Standard (AES) – se crede ca va fi mai bun ca DES (si 3 DES) 28

DES – Mod de functionare § Criptarea si decriptarea utilizeaza aceeasi cheie k – decriptarea este reversul criptarii § Algoritm lucreaza pe blocurilor de date de 64 de biti pe baza unei chei de 56 de biti. § 16 runde de criptare § Permutare initiala IP si finala FP § Blocul spart in 2 blocuri de 32 biti prelucrate alternativ – schema Feistel § Initial proiectat pt incriptare hardware § Sigur pt scopuri comerciale § Un calculator foarte puternic poate sparge DES prin forta bruta 29

DES – Mod de functionare § Algoritm pt. criptarea si decriptarea blocurilor de date de 64 de biti pe baza unei chei de 56 (64) de biti. • Blocul de criptat: 1) Permutare initiala IP 2) Calcul complex care depinde de cheie = o functie f functia de criptare (Feistel), si o functie KS planificarea cheii (selecteaza 56 de biti) 3) Permutare inversa a cele initiale FP = IP-1 1 2 3 Bloc Left Right 30

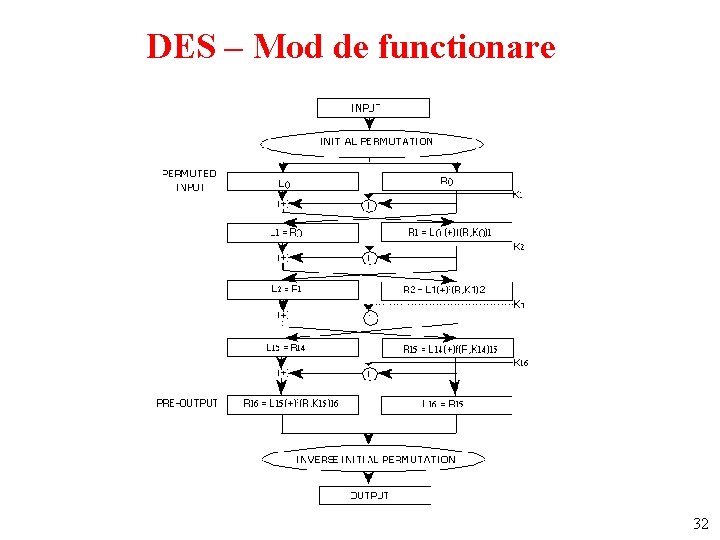
DES – Mod de functionare 2) Calcul § 16 iteratii; functia f opereaza asupra a 2 blocuri: unul de 32 biti si unul de 48 de biti un bloc de 32 de biti § Blocul de intrare = 64 biti = L (32) R (32) § K – un bloc de 48 biti ales din cheia KEY de 56 biti § La fiecare iteratie, blocul K este diferit Kn = KS(n, KEY) n [1, 16], Kn – functie care permuta o selectie de biti din KEY § Pt un bloc Ln-1 Rn-1, iesirea Ln. Rn a unei iteratii este: Ln = Rn-1 Rn = Ln-1 f(Rn-1, Kn) 31

DES – Mod de functionare 32

DES – Mod de functionare Functia de criptare (f) § E (bloc de 32) Cheie (48) – produce 32 biti § 4 etape: § Expansiune – permutare de expansiune E de la 32 la 48 § Mixare cheie – XOR cu 48 biti din cheie – planif cheie (16 subchei) § Substitutie – 8 bucati de 6 biti – 8 bucati de 4 biti – transformare neliniara – tabela de substitutie § Permutare – biti rearanjati printr-o permutare finala § Alternarea substitutiei cu permutarea si expansiunea creeaza “confuzie si difuzie” – Shannon 33

DES – Mod de functionare Planificarea cheii § Permuta cheia de 64 – PC 1 § Selecteaza 56 biti initial § Impart in 2 bucati de 28 biti § La fiecare runda ambele bucati sunt rotite la stanga cu 1, 2 biti si apoi selectez subcheia de 48 de biti printr-o functie de permutare PC 2: 24 biti din stanga si 24 biti din dreapta 34

DES – Atac Cheia: 56 biti – de incercat 72, 057, 594, 037, 927, 936 chei posibile § 1998 - Electronic Frontier Foundation (EFF) Au construit un calculator dedicat DESCHALL care poate decripta un mesaj care incearca toate cheile posibile in mai putin de 3 zile. Cost calculator: < $250, 000 Cauta 88 miliarde chei/sec § COPACOBANA = Cost Optimized Parallel Code Breaker – Germania 35

DES – Modele de operare • ECB – Electronic Codebook – DES direct • CBC – Cipher Block Chaining – DES extins care inlantuie blocuri de text incifrat • CFB – Cipher Feedback – utilizeaza text incriptat anterior ca intrare pt. DES si genereaza iesiri care sunt combinate cu textul neincriptat pentru a produce text incriptat • TDES – Triple Data Encryption Standard 36

Triple DES Triple-DES – dupa ce s-a aratat vulnerabilitatea DES Foloseste 3 chei DES de 56 biti – lungime cheie totala 168 biti 1. Incriptare folosind DES cu prima cheie de 56 biti 2. Incriptare folosind DES cu a doua cheie de 56 biti 3. Incriptare folosind DES cu a treia cheie de 56 biti Decriptarea la fel, in sens invers 37

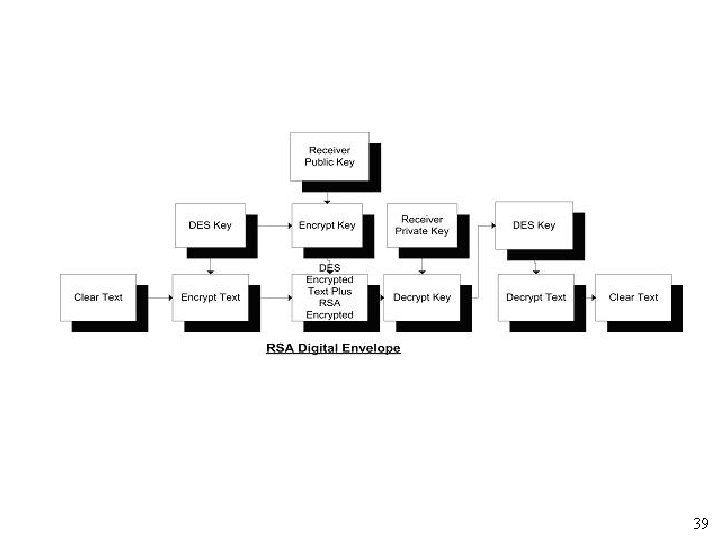
9 Sisteme combinate • RSA si DES pot fi folosite impreuna • DES – viteza mare, RSA – management convenabil • Un mesaj incriptat cu DES • Emitatorul utilizeaza cheia publica (RSA) a receptorului pt incriptarea cheii DES • Mesajul DES incriptat + cheia DES incriptata cu RSA sunt trimise receptorului intr-un plic digital RSA. • Cand plicul este primit de receptor, receptorul decripteaza cheia DES cu cheia lui RSA privata apoi utilizeaza cheia DES pt decriptare mesaj. 38

39

• Criptarea conventionala – cam de 1, 000 de ori mai rapida decat cea publica • O cheie conventionala de 80 biti este echivalenta ca putere cu o cheie publica de 1024 biti • O cheie conventionala de 128 biti este echivalenta ca putere cu o cheie publica de 3000 biti 40

PGP (Phil Zimmermann, 1991) • PGP combina avantajele sistemelor publice si conventionale • Criptosistem hibrid • Intai comprima textul • De ce? • Mai scurt, mai repede de transmis • Creste securitatea prin eliminarea sabloanelor • (fisierele care sunt prea scurte sau care nu se comprima bine nu sunt comprimate) 41

• PGP creaza o cheie de sesiune, o cheie secreta “onetime-only”. • Cheia – numar aleator generat pe baza miscarilor mouse si taste apasate • Se foloseste cheia intr-un sistem conventional • Cheia de sesiune se incripteaza cu cheia publica a receptorului • Se transmite cheia de sesiune criptata + textul incriptat • Decriptarea - invers 42

Certificat digital PGP Un certificat PGP: • Numarul versiunii PGP — identifica versiunea de PGP utilizata pentru crearea cheii asociata certificatului • Cheia publica din certificat a persoanei — cheia publica + algoritmul cheii: RSA, DH (Diffie-Hellman), or DSA (Digital Signature Algorithm). • Informatii referitor la persoana —nume, id, poza, etc. • Semnatura digitala a proprietarului certificatului —selfsignature – semnatura ce utilizeaza cheia privata corespunzatoare cheii publice din certificat • Perioada de validitate a certificatului — data de incepere a validitatii si data de expirare • Algoritmul de criptare simetric preferat pentru cheie — CAST, IDEA or Triple-DES. 43