Sistemas Periciais Tradicionais Funcionam assumindo que tudo Verdadeiro

Sistemas Periciais Tradicionais Funcionam assumindo que tudo é Verdadeiro ou Falso Qualquer regra cujas condições sejam satisfeitas é disparável as suas conclusões são Verdadeiras Estas assunções são simplistas e conduzem a Sistemas Periciais Frágeis 1 Sistemas Periciais com Conhecimento Incerto

Fontes de Incerteza • Informação incompleta • Informação imprecisa Raciocínio com Incerteza exige: • Quantificação de Incerteza • Método de combinação dos valores de Incerteza 2 Sistemas Periciais com Conhecimento Incerto

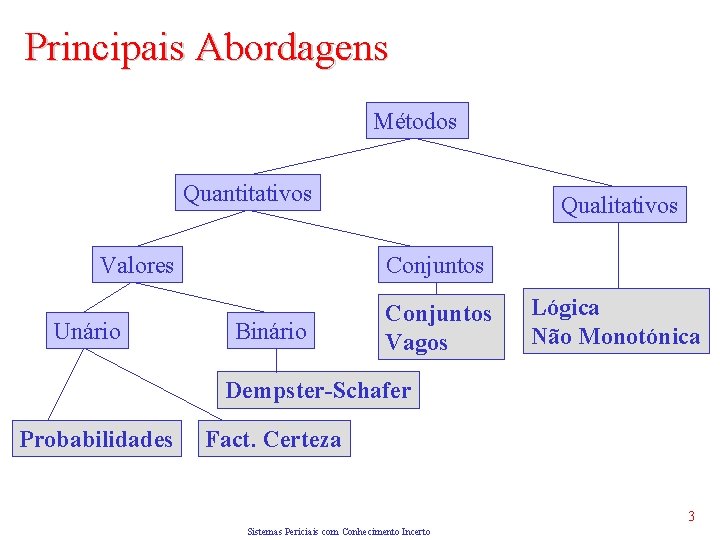
Principais Abordagens Métodos Quantitativos Valores Unário Qualitativos Conjuntos Binário Conjuntos Vagos Lógica Não Monotónica Dempster-Schafer Probabilidades Fact. Certeza 3 Sistemas Periciais com Conhecimento Incerto

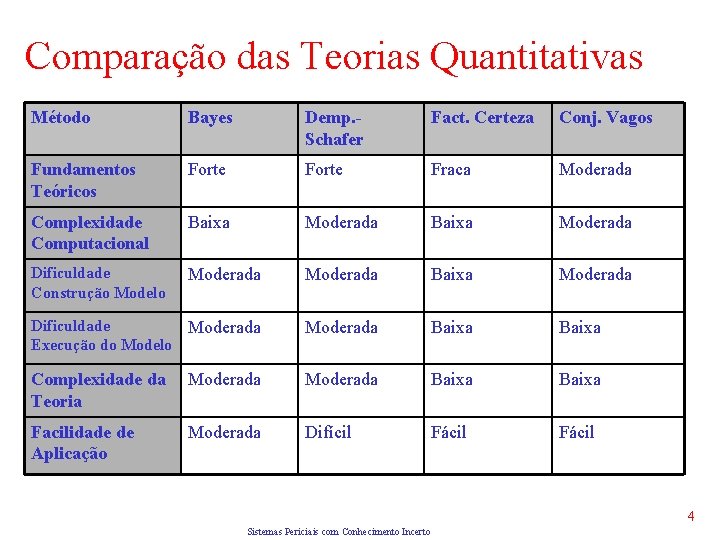
Comparação das Teorias Quantitativas Método Bayes Demp. Schafer Fact. Certeza Conj. Vagos Fundamentos Teóricos Forte Fraca Moderada Complexidade Computacional Baixa Moderada Dificuldade Construção Modelo Moderada Baixa Moderada Dificuldade Moderada Execução do Modelo Moderada Baixa Complexidade da Teoria Moderada Baixa Facilidade de Aplicação Moderada Difícil Fácil 4 Sistemas Periciais com Conhecimento Incerto

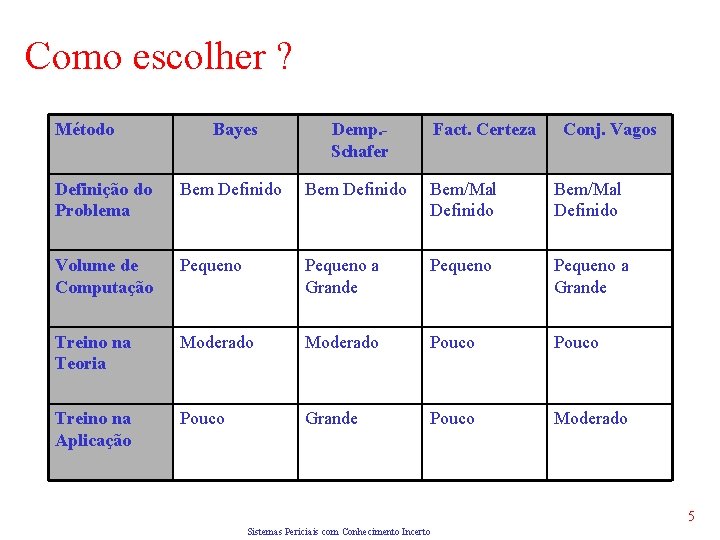
Como escolher ? Método Bayes Demp. Schafer Fact. Certeza Conj. Vagos Definição do Problema Bem Definido Bem/Mal Definido Volume de Computação Pequeno a Grande Treino na Teoria Moderado Pouco Treino na Aplicação Pouco Grande Pouco Moderado 5 Sistemas Periciais com Conhecimento Incerto

Fontes de Incerteza Dada a regra R 1: Se A & B então C Existem três potenciais áreas de Incerteza: – Incerteza nos dados (quão verdadeiros são A e B) – Incerteza na regra (com que frequência A & B implicam C) – Imprecisão em geral • As duas primeiras podem ser tratadas usando Probabilidades • A terceira usando Lógica Fuzzy 6 Sistemas Periciais com Conhecimento Incerto

Teoria da Probabilidade • É uma aproximação matemática para processar informação incerta • As suas raízes remontam ao séc. XVII, foi criada por um grupo de jogadores franceses, com o intuito de tornar o jogo menos aleatório • Mais tarde Pascal e Fermat desenvolveram a Teoria da Probabilidade Clássica – usada ainda hoje para extrair inferências numéricas de dados • Propõe a existência de um valor P(E) – Probabilidade - que consiste na possibilidade de ocorrência de um evento E a partir de uma experiência de eventos aleatórios • Ou seja, se realizarmos uma determinada experiência um número considerável de vezes, então podemos ter quase a certeza que a frequência relativa do evento E é aproximadamente igual a P(E) • O conjunto de todos os possíveis resultados de uma experiência é denominado espaço da amostra S. 7 Sistemas Periciais com Conhecimento Incerto

Probabilidade Discreta Experiências com resultados discretos P(E) = W(E)/N em que W(E) – nº de vezes que um particular evento Ocorreu N – nº de experiências realizadas Exemplo Considere-se o seguinte espaço resultante da experiência de rodar uma moeda S = {1, 2, 3, 4, 5, 6} Cada evento neste espaço da amostra representa um possível resultado da experiência. N será o número de vezes que a moeda é rodada e W(E) o número de resultados de um particular evento. A probabilidade de cada evento neste espaço P(E) =W(E)/N = 1/6 Sistemas Periciais com Conhecimento Incerto 8

Probabilidade Contínua Espaços contínuos Em vez de calcular a probabilidade de um evento a partir de um conjunto discreto eventos, existe necessidade de calcular valores intermédios a partir de um conjunto de valores contínuos. Daí que seja necessário uma função de calculo da probabilidade da distribuição do evento. 9 Sistemas Periciais com Conhecimento Incerto

Probabilidade Contínua Probabilidade experimental Define a probabilidade de um evento P(E) como o limite de uma função de frequência de distribuição f(E) P(E) = lim f(E)/N N sendo f(E) – frequência de observação de um evento Este tipo de probabilidade é também conhecido por probabilidade à posteriori – o que significa – “após o evento”. 0 < = P(E) <= 1 P(Ei) = 1 i P(E) + P(~E) = 1 sendo ~E o complemento de E Sistemas Periciais com Conhecimento Incerto 10

Probabilidades Compostas Em muitos problemas é necessário considerar combinações de diferentes eventos, por exemplo, calcular a probabilidade de ocorrência de dois eventos diferentes, ou a probabilidade de nenhum deles ocorrer. Intersecção Para problemas relativos a múltiplos eventos, é necessário determinar a intersecção dos espaços das amostras de todos os eventos. A partir disto é possível determinar a probabilidade conjunta eventos P(A B) = n(A B) / n(S) = P(A) * P(B) fórmula válida para independentes sendo P(A) = n(A)/n(S) Exemplo Considere-se a probabilidade de retirar do conjunto S = {1, 2, 3, 4, 5, 6} um número ímpar e um número divisível por 3 – dois eventos independentes. A= {1, 3, 5} B={3, 6} A B ={ 3} P(A) = 3/6 P(B) = 2/6 P(A B) = 1/6 Donde, a probabilidade de retirar do conjunto um número ímpar e divisível por 3 é 11 de 1/6. Sistemas Periciais com Conhecimento Incerto

Probabilidades Compostas União Por vezes pode ser necessário determinar a probabilidade de nenhum ou vários eventos ocorrerem P(A B) = P(A) + P( B) - P(A B) Exemplo Considere-se a probabilidade de retirar do conjunto S = {1, 2, 3, 4, 5, 6} um número ímpar ou um número divisível por 3 – dois eventos independentes. A= {1, 3, 5} B={3, 6} A B ={ 3 } P(A) = 3/6 P(B) = 2/6 P(A B) = 1/6 ou P(A B) = 3/6 + 2/6 – 1/6 = 2/3 Donde, a probabilidade de retirar do conjunto um número ímpar ou divisível por 3 é de 2/3. 12 Sistemas Periciais com Conhecimento Incerto

Probabilidade Condicional São usadas quando os eventos não são mutuamente exclusivos, ou seja, quando os eventos se podem influenciar. A probabilidade de ocorrência de um evento A sabendo que um evento B ocorreu é chamada Probabilidade Condicional e é dada por: P(A | B) = P(A B) / P(B) A probabilidade condicional permite obter a probabilidade de um evento A sabendo que o evento B ocorreu Exemplo Qual a probabilidade de se retirar do conjunto S o número 3 (evento A) sabendo que um número divisível por 3 ocorreu (evento B) P (A | B) = n (A B) / n (S) / n(B)/n(S) = n (A B) / n ( B ) = 1/6 / 2/6 = 1/2 13 Sistemas Periciais com Conhecimento Incerto

Fórmulas Básicas de Probabilidade Regra do Produto: Probabilidade de conjunção de dois eventos A e B Regra da Soma: Probabilidade de disjunção de dois eventos A e B Teorema da Multiplicação de Probabilidades: permite calcular a probabilidade de ocorrência simultânea de vários eventos a partir das probabilidades condicionais P(A 1 . . . An ) = P(An /A 1 . . . An-1). . . P(A 2 /A 1) P(A 1) 14 Sistemas Periciais com Conhecimento Incerto

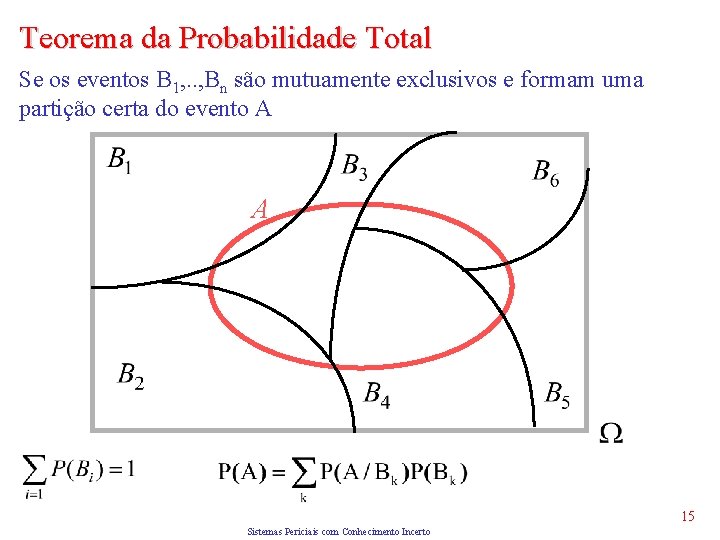
Teorema da Probabilidade Total Se os eventos B 1, . . , Bn são mutuamente exclusivos e formam uma partição certa do evento A A 15 Sistemas Periciais com Conhecimento Incerto

Probabilidade à Posteriori A probabilidade condicional permite obter a probabilidade de um evento A sabendo que o evento B (anterior a A) ocorreu Muitas vezes estamos interessados na situação inversa: Qual é a probabilidade de um anterior evento ter ocorrido sabendo que um evento posterior ocorreu ? Probabilidade à Posteriori O problema em determinar a probabilidade à posteriori foi resolvido por Thomas Bayes sendo conhecido por Teorema de Bayes 16 Sistemas Periciais com Conhecimento Incerto

Teorema de Bayes 1. P(h | D): probabilidade à posteriori de h dado D (reflecte a confiança da hipótese h depois de se observar – D) 2. P(D | h): probabilidade de D dado h • P(h): probabilidade a priori da hipótese h (representa o conhecimento de domínio, se este conhecimento prévio não existir pode ser atribuída a mesma probabilidade a cada hipótese candidata) 1. P(D): probabilidade a priori de D (sem conhecimento prévio) 17 Sistemas Periciais com Conhecimento Incerto

Teorema de Bayes A aplicação do teorema de Bayes como classificador requer que se conheçam: • duas probabilidades a priori - p (decisãoi) • uma probabilidade condicional - p (x | decisãoi) Em recursos ricos estatisticamente, é possível determinar a probabilidade das hipóteses serem verdadeiras, através de algumas evidências acerca do problema 18 Sistemas Periciais com Conhecimento Incerto

Teorema de Bayes O Teorema de Bayes é usado no desenvolvimento de Sistemas Periciais Dada a estrutura de uma regra típica If E then H (LS, LN) A fórmula de Bayes pode ser usada para calculo da probabilidade da hipótese H partindo da probabilidade apriori do facto E Exemplo: Diagnóstico de avaria de uma máquina. Podemos observar os sintomas apresentados pela máquina mas o diagnóstico está relacionado com os eventos anteriores que causaram os sintomas que a máquina apresenta 19 Sistemas Periciais com Conhecimento Incerto

LS versus LN As regras são da forma IF E THEN H (LS, LN) E – denota alguma Evidência H – representa alguma Hipótese LS – Likelihood of Sufficiency representa a medida de Suporte da Hipótese H dada a Evidência E LS = P(E | H) / P(E |~H) LN– Likelihood of Necessity representa a medida de descredito da Hipótese H se a Evidência E estiver em falta LN = P(~E | H) / P(~E | ~H) 20 Sistemas Periciais com Conhecimento Incerto

LS versus LN IF E THEN H (LS, LN) Ambos os factores LS e LN são fornecidos pelo perito e são usados para calcular a Probabilidade à Posterior da Hipótese O ( H | E ) Ambos os factores variam : 0 < LS < 0 < LN < LS Efeito na Hipótese 0 Pequeno 1 Grande H é Falso quando E é Verd ou ~E é necessário para concluir H E não é favorável para concluir H E não tem efeito para concluir H E é favorável para concluir H E é logicamente suficiente para concluir H 21 Sistemas Periciais com Conhecimento Incerto

LS versus LN LN Efeito na Hipótese 0 Pequeno 1 Grande H é Falso quando E ausente ou E é necessário para concluir H Ausência de E não é favorável para concluir H Ausência de E não tem efeito para concluir H Ausência de E é favorável para concluir H Ausência de E é logicamente suficiente para concluir H 22 Sistemas Periciais com Conhecimento Incerto

Aplicação do Teorema de Bayes: Diagnóstico Médico P(M|S) = P(S|M)P(M) Seja P(S) M = doença meningite S = dor no pescoço 1 Probabilidade condicional Um Doutor sabe: P(S|M) = 0. 5 2 Probabilidades a priori P(M) = 1/50000 = 0, 5*(1/50000) = 0, 0002 1/20 A probabilidade de uma pessoa ter meningite dado que ela está com dor no pescoço é 0, 02% ou ainda 1 em 5000. P(S) = 1/20 23 Sistemas Periciais com Conhecimento Incerto

Exercício Pacientes com problemas cardíacos são sujeitos a um electrocardiograma (ECG) Os resultados são classificados: • positivos (+ECG) sugerindo doença cardíaca (+DC) • negativos (-ECG) no caso de não haver doença cardíaca (-DC) Assumindo que um dado paciente realizou um electrocardiograma positivo pretende-se saber qual a probabilidade deste ter doença cardíaca ? P(+DC | + ECD) Sabendo que – 10 pessoas em 100 têm um ataque cardíaco – 90 pessoas em 100 que tiveram doença cardíaca produziram um electrocardiograma positivo – 95 pessoas em 100 que não tiveram doença cardíaca produziram um electrocardiograma negativo 24 Sistemas Periciais com Conhecimento Incerto

Exercício • 10 pessoas em 100 têm um ataque cardíaco P(+DC) = 0. 1 P(-DC) = 1 - P(+DC) = 1 - 0. 1 = 0. 9 • 90 pessoas em 100 que tiveram doença cardíaca produziram um electrocardiograma positivo (+ECD) P(+ECD | +DC) = 0. 9 • 95 pessoas em 100 que não tiveram doença cardíaca produziram um electrocardiograma negativo (-ECD) P ( -ECD | -DC) = 0. 95 P (+ECD | -DC) = 1 - P(-ECD | -DC) = 1 - 0. 95 = 0. 05 P(+ECD) = P(+ECD | +DC) * P(+DC) + P(+ECD | -DC) * P(-DC) = 0. 9 * 0. 1 + 0. 05 * 0. 9 = 0, 135 P(+DC | + ECD) = P(+ECD | +DC) * P(+DC) / P(+ECD ) P(+DC | + ECD) = 0. 1 * 0. 9 / 0, 135 = 0. 67 67% 25 Sistemas Periciais com Conhecimento Incerto

Teorema de Bayes A aplicação do teorema de Bayes requer que se conheçam: • duas probabilidades a priori - p (decisãoi) • uma probabilidade condicional - p (x | decisãoi) Na prática estas probabilidades são desconhecidas • Estimativas fiáveis destas probabilidades requer um número infinito de exemplos Como ultrapassar o problema ? – Assumindo simplificações no calculo de p (x | decisão) O termo P(D) também pode ser escrito sob a forma: P(D) = P(D | h) * P(h) + P(D | ~h) * P(~h) 26 Sistemas Periciais com Conhecimento Incerto

Teorema de Bayes Generalizado • • Conjunto de evidências Ei Conjunto de Hipóteses plausíveis Hj Assumindo que as hipóteses são – mutuamente exclusivas e – colectivamente exaustivas Suposição Bayesiana Naive P (a 1, a 2, . . . , an / vj) = P (ai / vj) i P (Hj | E 1. . Em) = P (Hi | E 1 , . . . , Em) * P(Hj ) 27 Sistemas Periciais com Conhecimento Incerto

PROSPECTOR - Sistema Pericial no domínio da Geologia • desenvolvido para auxiliar os geólogos na procura de depósitos minerais [Duda-79] • Um dos Sistemas Periciais mais populares de Aplicação da Teoria Bayesiana para Apoio à Decisão • Dado o sucesso deste Sistema Pericial surgiu a Linguagem KAS que permite o desenvolvimento de Sistemas Periciais usando a Teoria Bayesiana de Probabilidades 28 Sistemas Periciais com Conhecimento Incerto

PROSPECTOR - Medida de Certeza Em vez de se usar P( E | E’) introduziram o conceito Medida de Certeza C ( E | E’) variável - 5 < C ( E | E’) < 5 Se C ( E | E’) = -5 então P ( E | E’) = 0 C ( E | E’) = 0 então P ( E | E’) = P(E) C ( E | E’) = 5 então P ( E | E’) = 1 Para P(E | E’total) > P(E) C(H|E’) = 5 * P(E | E’total) – P(E) / 1 -P(E) Para P(E | E’total) <= P(E) C(H|E’) = 5 * P(E | E’total) – P(E) / P(E) A razão principal para introduzir este conceito prendeu-se meramente com questões psicológicas. É mais fácil para um perito dizer: “Penso que estou a apanhar uma constipação” Do que dizer: “A probabilidade de estar a apanhar uma constipação é de 90%” 29 Sistemas Periciais com Conhecimento Incerto

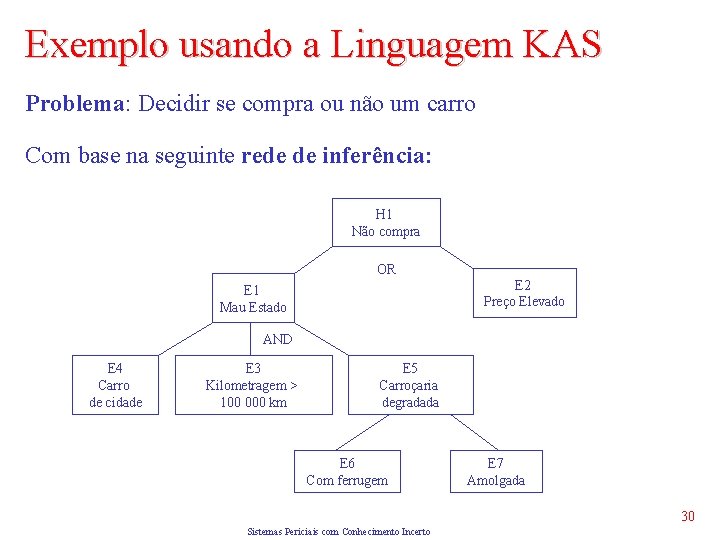
Exemplo usando a Linguagem KAS Problema: Decidir se compra ou não um carro Com base na seguinte rede de inferência: H 1 Não compra OR E 2 Preço Elevado E 1 Mau Estado AND E 4 Carro de cidade E 3 Kilometragem > 100 000 km E 5 Carroçaria degradada E 6 Com ferrugem E 7 Amolgada 30 Sistemas Periciais com Conhecimento Incerto

Exemplo Regras que formam a rede de inferência Regra R 1 Se Carro em Mau Estado Ou Preço do carro Elev Então Não compra carro Regra R 2 Se Kilometragem do carro > 100 000 Km E Carro de cidade E carroçaria degradada Então carro em mau estado Regra R 3 Se carro tem amolgadelas Então carroçaria degradada [LS = 1000, LN = 0. 001] Regra R 4 Se carro tem ferrugem Então carroçaria degradada [LS = 100, LN = 1] 31 Sistemas Periciais com Conhecimento Incerto

Exemplo Regra R 3 Se carro tem amolgadelas Então carroçaria degradada [LS = 1000, LN = 0. 001] Regra R 4 Se carro tem ferrugem Então carroçaria degradada [LS = 100, LN = 1] A presença de amolgadelas no carro é muito favorável à conclusão Carroçaria degradada, enquanto que a não observação de amolgadelas é bastante desfavorável no suporte da conclusão No caso da regra R 4 a ferrugem é de algum modo favorável ao suporte da conclusão, enquanto que a ausência de ferrugem não tem qualquer efeito na conclusão 32 Sistemas Periciais com Conhecimento Incerto

Exemplo Assumindo que todas as Probabilidades à priori das Evidências P( Ei ) = 0, 1 Sistema KAS com que Grau de Confiança se pode assumir que: 1. 2. 3. 4. a Kilometragem do carro é superior 100 000 Km ? o carro é de cidade ? o carro tem amolgadelas ? o carro tem ferrugem ? 5. o preço do carro é elevado ? Utilizador: 5 Utilizador: 4 Utilizador: -1 Utilizador: 1 Conclusão: A minha certeza em não comprar o Carro é de 3. 97 O valor da Confiança C(H 1) = 3. 97 com base no intervalo [-5, 5] Sendo o valor mais próximo de 5 conclui-se “Recomenda-se vivamente a não comprar o carro” 33 Sistemas Periciais com Conhecimento Incerto

Operações Internas C(E 3 | E 3’) = C(E 4 | E 4’) = 5 o utilizador observando E 3’ e E 4’ está totalmente certo de E 3 e E 4 C(E 5 | E 6, E 7) ? É calculado através do Teorema Bayes por manipulação das diversas fórmulas de Probabilidades C(E 5 | E 6, E 7) = 3, 97 A confiança em E 1 é dada pela conjunção das condições E 3, E 4, E 5, pelo que C(E 1) = min {5, 5, 3, 97} = 3, 97 A confiança em H 1 é dada pela disjunção das condições E 1 e E 2 C(H 1) = max {3, 97, 1} = 3, 97 Sistemas Periciais com Conhecimento Incerto 34

Inconvenientes da Abordagem Bayesiana • • • Só é matematicamente correcta se os eventos respeitarem a independência estatística Requer a existência de valores difíceis de obter – Probabilidades à Priori Não admite incerteza associada às evidências Alguns problemas em que os dados ou a informação está continuamente a ser alterada é necessário recalcular as probabilidades Em bases de conhecimento de dimensão apreciável, torna-se difícil efectuar alterações dado que se tem de verificar P(H 1) + P(H 2) +. . . + P(Hn) = 1 35 Sistemas Periciais com Conhecimento Incerto