Sistemas de Funciones Iteradas IFS Carlos Reynoso UNIVERSIDAD

Sistemas de Funciones Iteradas IFS Carlos Reynoso UNIVERSIDAD DE BUENOS AIRES billyreyno@hotmail. com

Objetivo • Presentar un formalismo generativo regido por álgebra – Contrastante con las gramáticas de sistemas-L o con las funciones fractales comunes • Examinar si hay posibilidad de uso antropológico • Tomar contacto con algunas experiencias que ya existen • Analizar las herramientas y recursos disponibles

Agenda • • Introducción al álgebra lineal Transformaciones afines Máquinas de copia de reducción múltiple Fractales de Sistemas de Funciones Iterativas • Programas y recursos • Diseños culturales de tipo IFS • Conclusiones y referencias

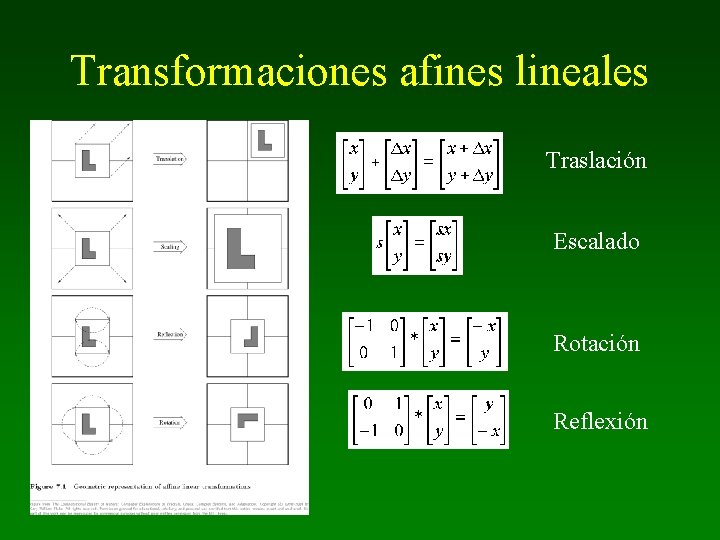
Transformaciones afines lineales Traslación Escalado Rotación Reflexión

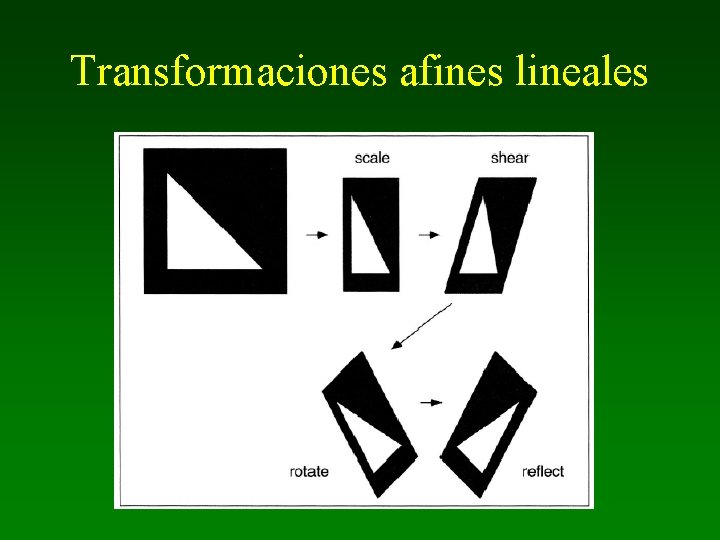
Transformaciones afines lineales

Algoritmo de Máquina de Copia de Reducción Múltiple (MCRM) • Se reduce la imagen original y se la ubica en alguna otra parte, iterativamente

Algoritmo de Máquina de Copia de Reducción Múltiple (MCRM) • Se reduce la imagen original y se la ubica en alguna otra parte, iterativamente

Algoritmo de Máquina de Copia de Reducción Múltiple (MCRM)

Al cabo de algunos pasos, la imagen original es irrelevante

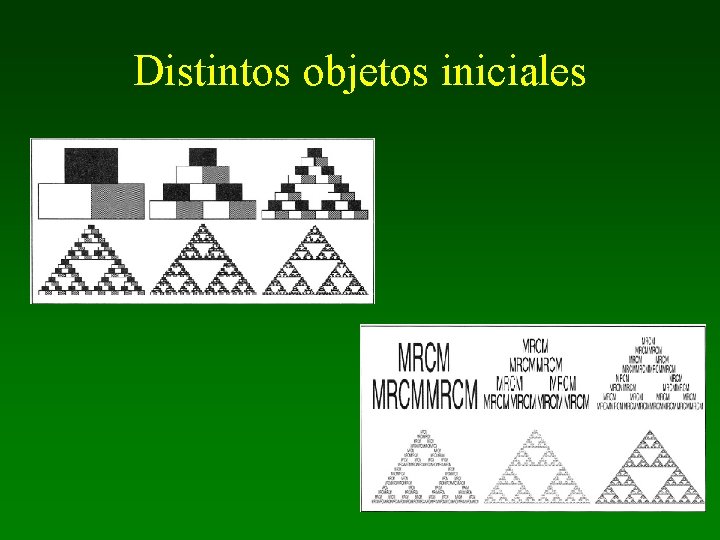
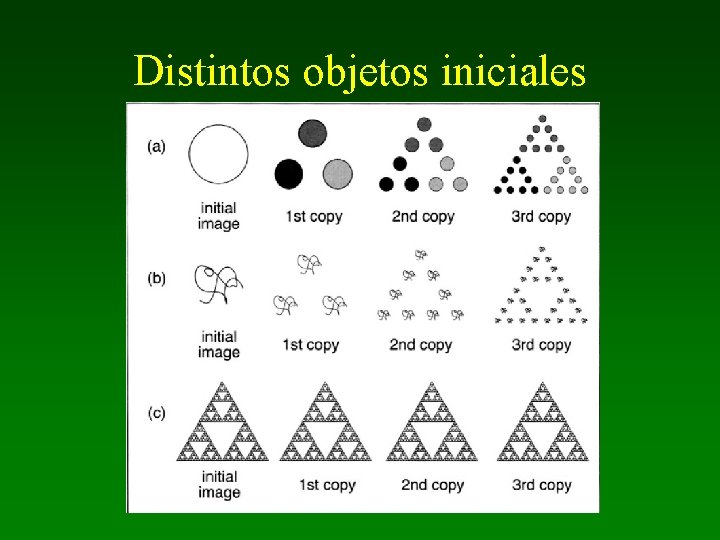
Distintos objetos iniciales

Distintos objetos iniciales

Reflexión colateral ¿Cuántas iteraciones? • Para que el objeto inicial sea irrelevante, se requieren 7 o más iteraciones • “El mágico número siete, más o menos dos” (Miller) • Las iteraciones son en realidad recursivas • Siete o más recursiones es mucho • Los objetos culturales más complejos tienen como mucho cuatro niveles de anidamiento

Sistemas de funciones iteradas • IFS – Define un conjunto de funciones contractivas – Cada punto es una copia de la imagen • Inventado por John Hutchinson (1981), popularizado por Michael Barnsley (Fractals everywhere, disponible) • Investigación en compresión fractal • También desarrollos de expansión de imágenes – Genuine Fractals Print. Pro para Adobe Photoshop

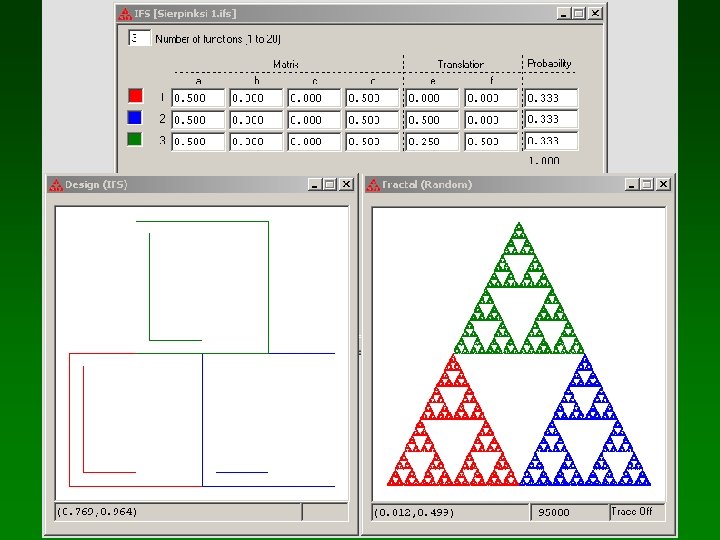
Juego del caos • Algoritmo para generar fractales IFS • Se toma un punto al azar en el plano y se le aplica una de las funciones definidas, también al azar, dibujando el punto correspondiente • Las imágenes que se forman son tan densas como iteraciones se especifiquen y probabilidad tenga la transformación • Caos = Fractal – Un IFS es un atractor extraño – Geométricamente un atractor extraño es un fractal; dinámicamente es un sistema caótico

Teorema del collage • Michael Barnsley – El “problema inverso” de la geometría fractal – Un problema inverso consiste en obtener los valores de parámetros a partir de los datos observados – Comenzar por la imagen y encontrar el IFS que converja en él – Para encontrar un IFS cuyo atractor “se parezca” a una imagen determinada, se debe localizar un conjunto de transformaciones afines (mapas de contracción) tal que la “suma” (o collage) del conjunto se asemeje al conjunto correspondiente – Encontrar contracciones tal que cada una de ellas sea una pequeña pieza del conjunto

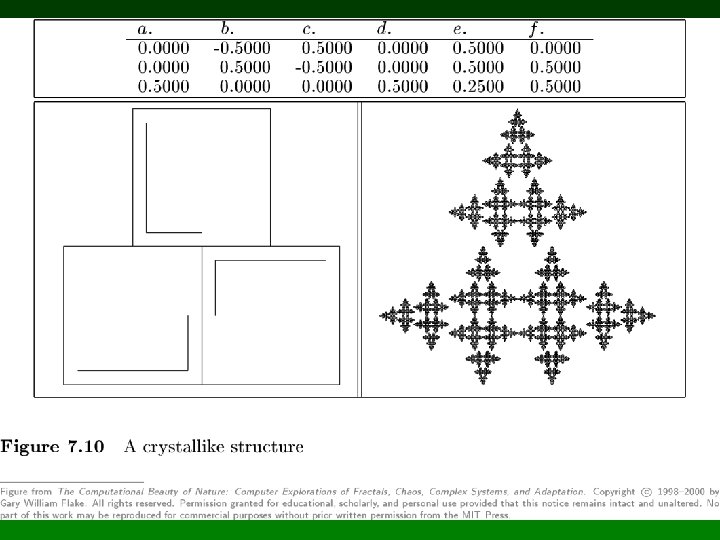
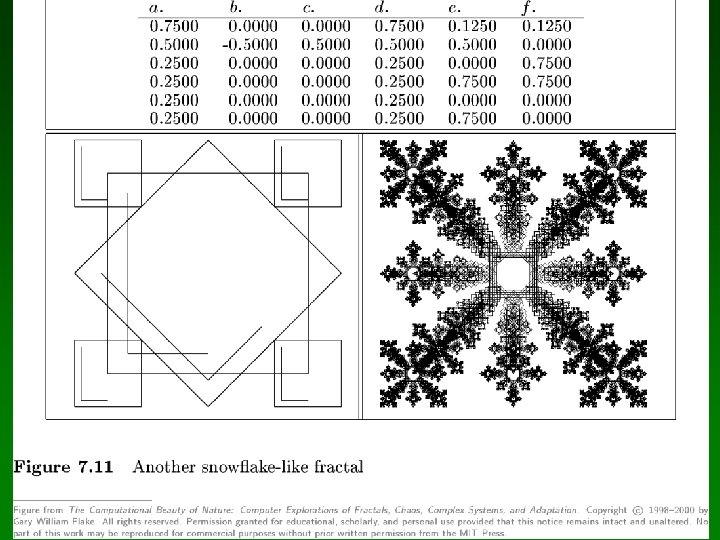
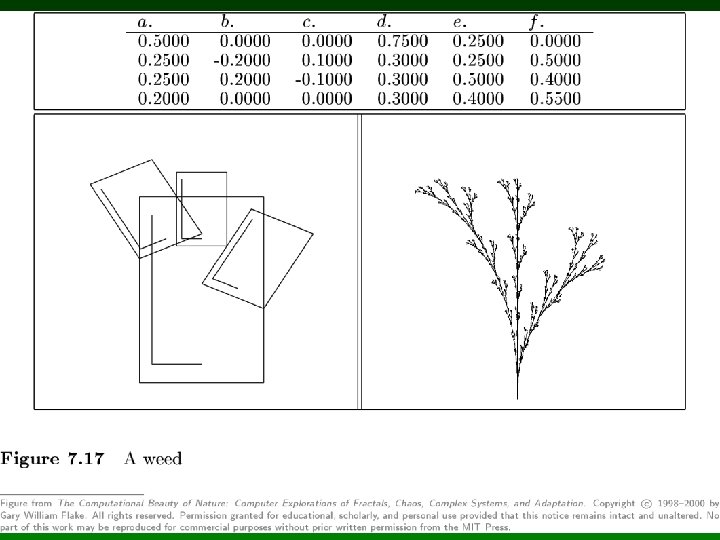
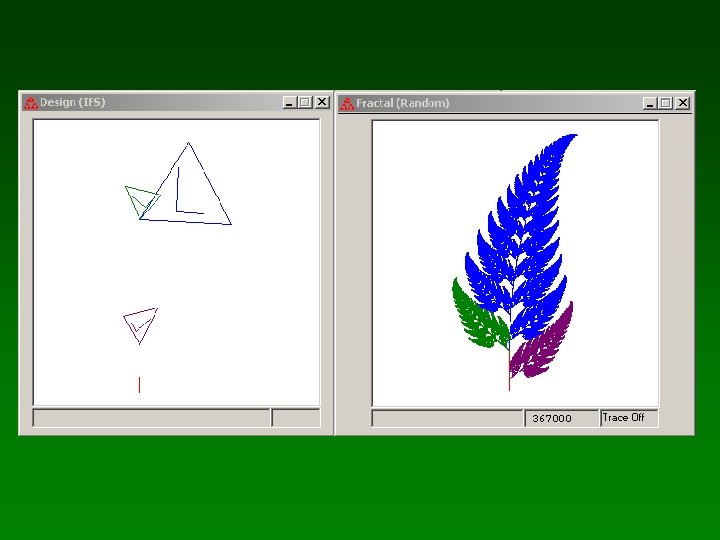
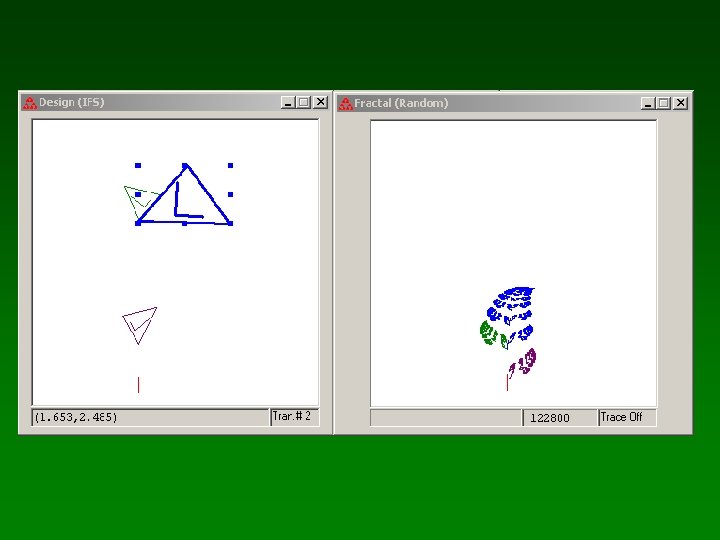
Ejemplos de IFS

Tipos de IFS especiales • IFS en 3 dimensiones • Flame fractals – – Algoritmo de Scott Daves, 1992 Extensión de IFS Histograma de un sistema complejo Agrega transformaciones no lineales • IFS para generación y análisis de música

Flame fractals - Binario

Flame fractals - Lineal

Flame fractals - Logarítmico

Flame fractals – Con color

Flame fractals – Con factor gamma

Flame fractals – Con colores vibrantes

Tipos de IFS especiales • Esponja de Menger • Versión tridimensional de alfombra de Sierpiński – Triángulo de Pascal • Analogías con polvo de Cantor y otros fractales • Estructuras “aireadas” de torre Eiffel

- Uruk - Diseños catedral de Anagni (s. XIII) - Escher, estudios sobre los patrones del púlpito de la catedral de Ravello (s. XII, 1923)

China, s. XIV Coeficientes binomiales hasta 8 a potencia

Arquitectura moderna mauritana en Casamance, Senegal (Eglash, p. 219)

Programas para trabajar con IFS Brazil • Brazil – Viejo, pero simple y práctico. Discontinuado. – No permite operar con matrices – Morphing. • IFS Fractal Designer IFSDesign – Discontinuado e incompatible, pero excelente. – IFS puro en 2 D con actualización de imagen en tiempo real. – Puramente analógico. No tiene editor de matrices. • Apophysis – Para diseño artístico, con componente de azar. – Editor de matrices en 3 D. Flame fractals

Programas para trabajar con IFS • IFS 3 D – Matrices en tres dimensiones – Sólo estructuras al azar, o a mano. Texturas polvorosas únicamente. Visualización 3 D en tiempo real. • Visions of Chaos – Fractales genéricos, con importante módulo de IFS. Altísima calidad gráfica. Mutaciones, pero no actualización cruzada en tiempo real. No se pueden tratar ni visualizar los vectores. – Formato de archivo compatible. Muchos ejemplos. • Xeno. Dream – Uno de los programas de fractales más evolucionados. No es estrictamente de IFS. No tiene matrices. • Fairy Brush 2, Dino. Coomy, Sprouts, Turban shell festive.

Xenodream (Imágenes)

IFS Construction Kit • Todavía está en desarrollo. • Es la elección para trabajar con pleno control analítico. • Matrices y vectores, con actualización cruzada (aunque no rendering en tiempo real). • Formato de archivo compatible con Vision of Chaos, Fractint, Chaos Pro, etc.

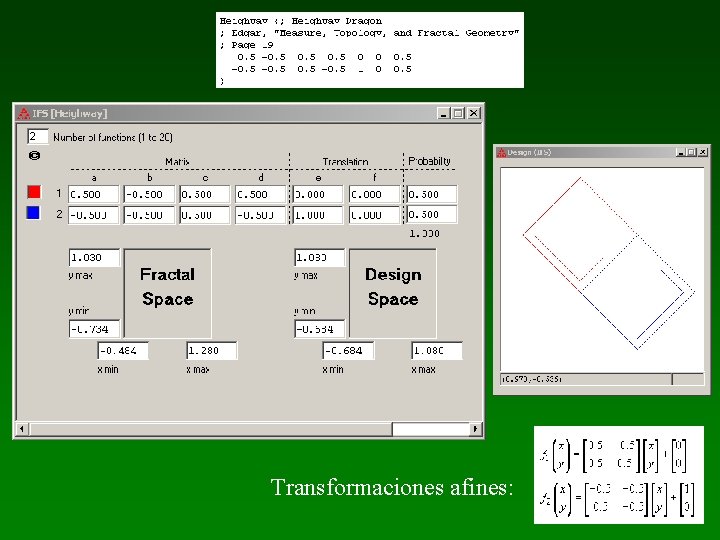
IFS Construction Kit

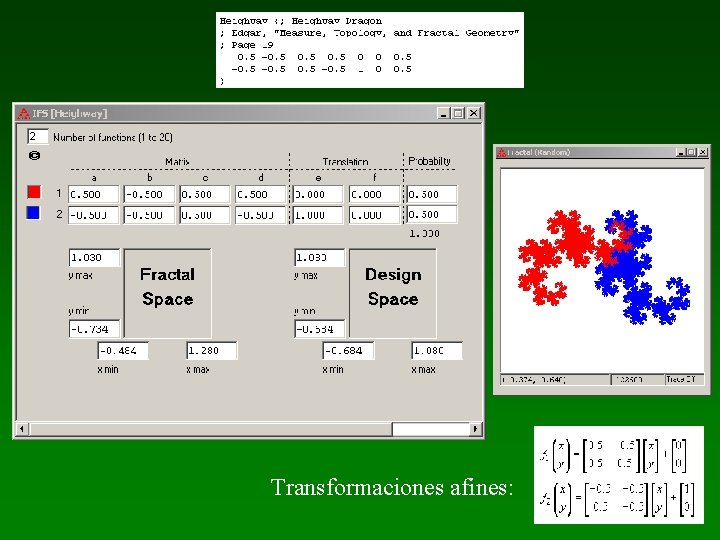
Transformaciones afines:

Transformaciones afines:

Dificultades • Ejercicio – Cargar Helecho importado de Visions of Chaos – Deformar sutilmente los triángulos – Verificar efectos – Ejecutar Billy-Cruz • Correr Determinista • Probabilista con probabilidades iguales • Idem, proporcionales

Parámetros idénticos en distintos programas

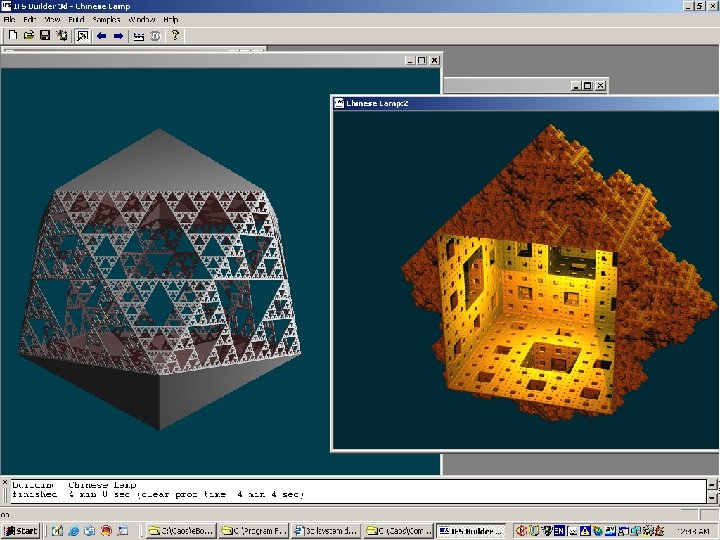
IFS Builder 3 D • Desarrollo ruso, reciente • Incorpora docenas de ejemplares de otros paquetes • Excelente reproducción tridimensional, controlable por código • No tiene edición analógica por matrices

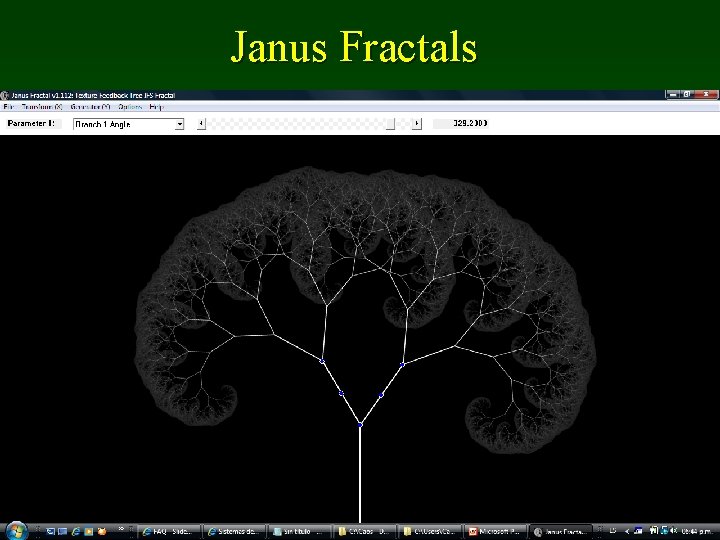
Janus Fractals • El más poderoso graficador orientado a IFS • No incluye manejo de matrices, ni objetos de vectoriales de control • Conjunto sobresaliente de tipos fractales • Edición puramente gráfica • Excelente representación tridimensional

Janus Fractals

Otros programas • Fractal DRAW Go – No es gratuito, aunque hay una versión de prueba que pasado un tiempo no deja guardar archivos – Es vistoso y puede ser útil para diseños figurativos limitados, pero no posee prestaciones analíticas – No se pueden situar las formas con precisión – Imposible migrar las figuras a otro contexto • IFS Lab – Prestaciones restringidas. – Buena herramienta para comprender generación de una máquina de reducción a partir de un dibujo (teorema del collage).

Diseños culturales (1/6) • Mostacillas Zulu – IFS + Simetrías

Diseños culturales (2/6) • Chonat Getz – Dra, Universidad de Witwatersrand – Simulaciones IFS de cestería Zulu • John Sims – Ringling School of Design, Florida – Patrones fractales iterativos en telas rafia Bakuba

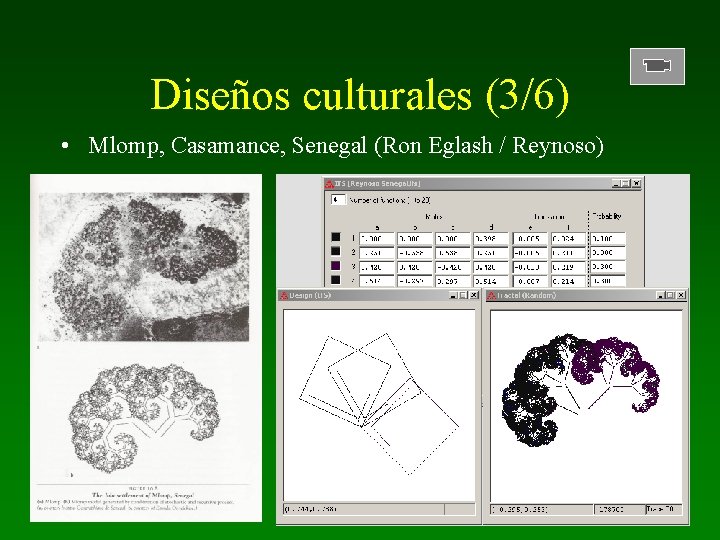
Diseños culturales (3/6) • Mlomp, Casamance, Senegal (Ron Eglash / Reynoso)

Diseños culturales (4/6) • Brian Meloon & Julien Sprott – – Cuantificación de determinismo en música usando IFS – Música al azar vs Mozart, Sonata en Do* – *¿ 279, 309, 330, 545?

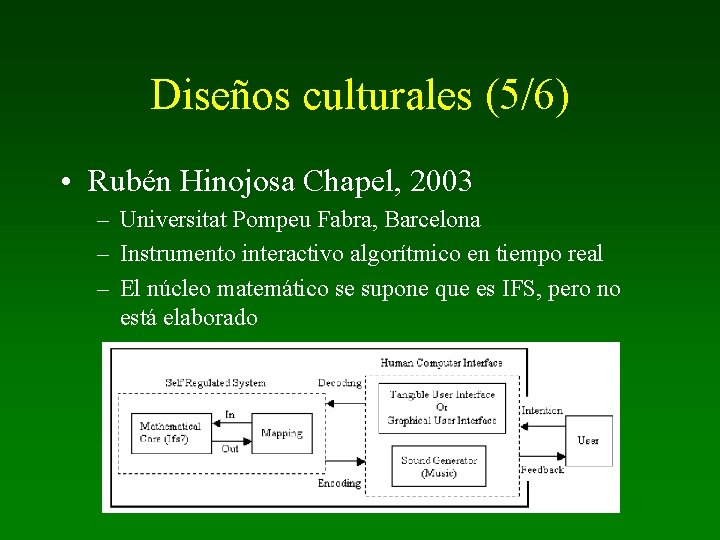
Diseños culturales (5/6) • Rubén Hinojosa Chapel, 2003 – Universitat Pompeu Fabra, Barcelona – Instrumento interactivo algorítmico en tiempo real – El núcleo matemático se supone que es IFS, pero no está elaborado

Diseños culturales (6/6) • A Musical Generator 3. 1 AMu. Gen

(Posibles) ejemplos arquitectónicos • Santa Croce, Firenze (Nicoletta Sala) – Maquiavelo, Miguel Angel, Rossini

Conclusiones (1/2) • Método para describir de forma compacta algunas imágenes autosimilares (por ej. patrones de asentamiento) • No es una bala de plata para toda ocasión – Reflexionemos sobre las balas de plata • No hay heurísticas para otras clases de objetos fuera del repertorio clásico

Conclusiones (2/2) • No sirve para imágenes idénticamente repetitivas: siempre tiene que haber contracción • Es difícil encontrar un conjunto de contracciones para un objeto determinado • Pocas elaboraciones antropológicas del asunto • A diferencia de sistemas-L no se puede vincular fácilmente con ideas emic • Las herramientas de IFS deben complementarse con sistemas-L y álgebra de grupos (simetrías)

Recursos • Software de Fractales/IFS, AMu. Gen 3. 1 • Michael Barnsley. Fractals everywhere, 1968 • Peitgen-Jurgens-Saupe. Chaos and fractals, new frontiers of science, 2 a ed. , 2004 • Rubén Hinojosa. Realtime algorithmic music systems from fractal and chaotic functions, 2003.

¿Preguntas? Carlos Reynoso UNIVERSIDAD DE BUENOS AIRES billyreyno@hotmail. com