Sistemas de Ecuaciones Lineales Glen D Rodrguez R








![Pivotear en GE • A = [ 0 1 ] falla por que no Pivotear en GE • A = [ 0 1 ] falla por que no](https://slidetodoc.com/presentation_image_h/cf0f0890660453e410622709fe965395/image-18.jpg)




















































- Slides: 111

Sistemas de Ecuaciones Lineales Glen D. Rodríguez R. Algoritmos Paralelos Basado en material de J. Demmel

Eliminación Gaussiana y matrices densas n n n Algebra lineal densa “Gaussian Elimination” (GE) para resolver Ax=b Optimizar GE para máquinas secuenciales con caché ¡ n n n Usando multiplicación matriz x matriz (BLAS) LAPACK Partición de la Data en comp. paralelas GE paralelo Sca. LAPACK Problemas de Eigenvalue

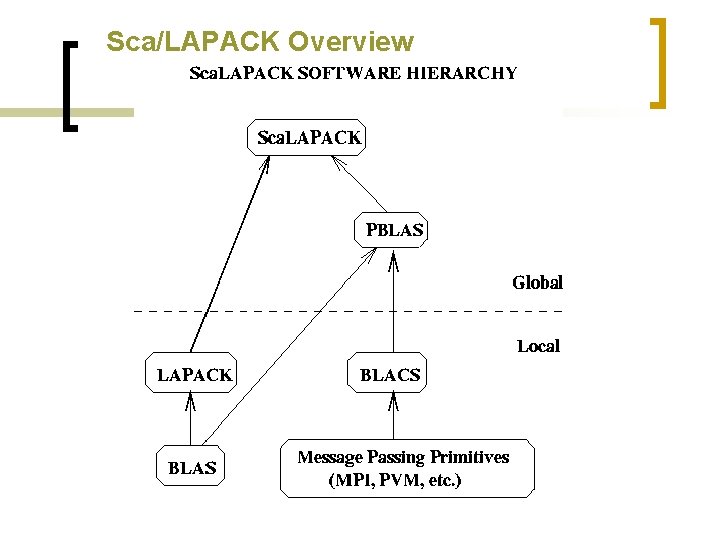
Sca/LAPACK Overview

Exitos usando Sca/LAPACK n n Muy usado: ¡ Adoptado por Mathworks, Cray, Fujitsu, HP, IBM, IMSL, NAG, NEC, SGI, … ¡ >56 M visitas en la web de Netlib (incl. CLAPACK, LAPACK 95) Descubrimientos hechos a través de la solución de sistemas de ec. densos ¡ Artículo en Nature sobre el universo plano usó Sca. LAPACK ¡ Otros en Physics Review B también lo usaron ¡ 1998 Premio Gordon Bell ¡ www. nersc. gov/news/reports/ne w. NERSCresults 050703. pdf Cosmic Microwave Background Analysis, BOOMERan. G collaboration, MADCAP code (Apr. 27, 2000). Sca. LAPACK

Usos de Solución de sistemas de ecuaciones lineales n n n n Resistencia de estructuras (ing. civil) Stress, tensiones en piezas mecánicas Electromagnetismo, electrodinámica Circuitos eléctricos Ing. de tráfico. DSP, óptica (de-convolución) Economía y finanzas.

Motivación (1) 3 problemas básicos de Alg. Lineal 1. 2. Ecuaciones Lineales: Resolver x en Ax=b Mínimos cuadrados: Hallar x que minimiza ||r||2 S ri 2 donde r=Ax-b n Estadística: Ajustar datos a funciones simples 3 a. Eigenvalues: Hallar l , x tal que Ax = l x Análisis de vibraciones (terremotos, circuitos) 3 b. Singular Value Decomposition: ATAx= 2 x n Ajuste de data, Obtención de información n Muchas variaciones para diferentes estructuras de A n Simétrica, definida positiva, en bandas, …

Motivación (2) n Por qué A densa, en vez de A dispersa? ¡ ¡ Muchas matrices grandes son dispersas, pero … Alg. Densos son más fáciles de entender Algunas aplicaciones producen matrices densas grandes LINPACK Benchmark (www. top 500. org) n ¡ “Qué tan rápida es tu computadora? ” = “Qué tan rápido resuelves Ax=b denso? ” Alg. de matriz dispersa grande con frecuencia producen menores (pero aún grandes) problemas densos.

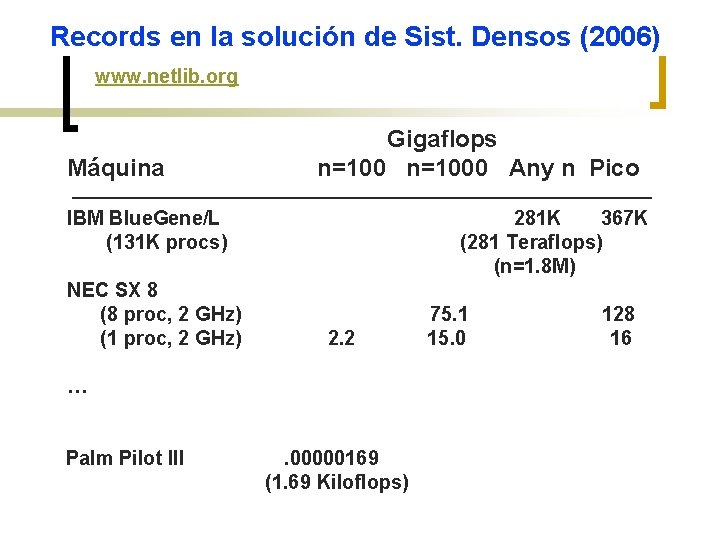
Records en la solución de Sist. Densos (2006) www. netlib. org Máquina Gigaflops n=1000 Any n Pico IBM Blue. Gene/L (131 K procs) NEC SX 8 (8 proc, 2 GHz) (1 proc, 2 GHz) 281 K 367 K (281 Teraflops) (n=1. 8 M) 2. 2 … Palm Pilot III . 00000169 (1. 69 Kiloflops) 75. 1 15. 0 128 16

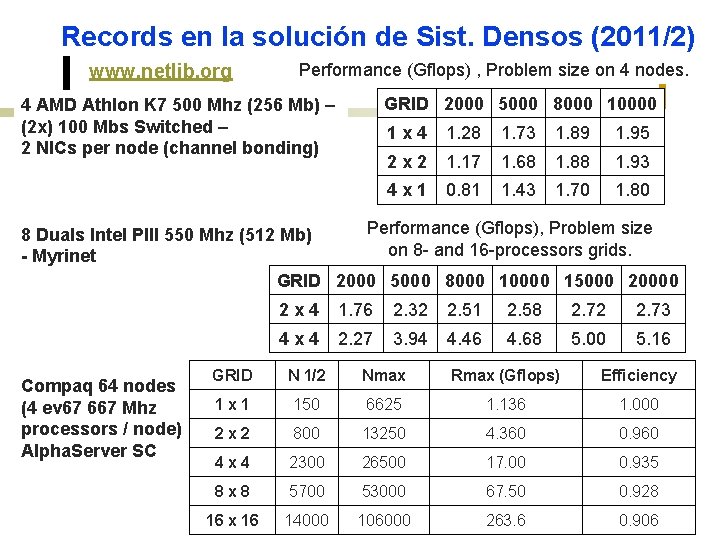
Records en la solución de Sist. Densos (2011/2) www. netlib. org Performance (Gflops) , Problem size on 4 nodes. GRID 2000 5000 8000 10000 4 AMD Athlon K 7 500 Mhz (256 Mb) – (2 x) 100 Mbs Switched – 2 NICs per node (channel bonding) 1 x 4 1. 28 1. 73 1. 89 1. 95 2 x 2 1. 17 1. 68 1. 88 1. 93 4 x 1 0. 81 1. 43 1. 70 1. 80 Performance (Gflops), Problem size 8 Duals Intel PIII 550 Mhz (512 Mb) on 8 - and 16 -processors grids. - Myrinet GRID 2000 5000 8000 10000 15000 20000 Compaq 64 nodes (4 ev 67 667 Mhz processors / node) Alpha. Server SC 2 x 4 1. 76 2. 32 2. 51 2. 58 2. 72 2. 73 4 x 4 2. 27 3. 94 4. 46 4. 68 5. 00 5. 16 GRID N 1/2 Nmax Rmax (Gflops) Efficiency 1 x 1 150 6625 1. 136 1. 000 2 x 2 800 13250 4. 360 0. 960 4 x 4 2300 26500 17. 00 0. 935 8 x 8 5700 53000 67. 50 0. 928 16 x 16 14000 106000 263. 6 0. 906

Eliminación Gaussiana (GE) en Ax=b n n Añadir múltiplos de cada fila a las demás para volver A en triangular sup. Resolver el sist. triang. resultante Ux = c por sustitución … para cada columna i … “cerear” debajo de la diagonal añadiendo múltiplos de la fila i a las de abajo for i = 1 to n-1 … para cada fila j debajo de la fila i for j = i+1 to n … añadir un multiplo de la fila i a la fila j tmp = A(j, i); for k = i to n A(j, k) = A(j, k) - (tmp/A(i, i)) * A(i, k) 0. . . 0 0 After i=1 After i=2 0. 0. 0 0 0 After i=3 … 0. 0. 0 0 0 After i=n-1

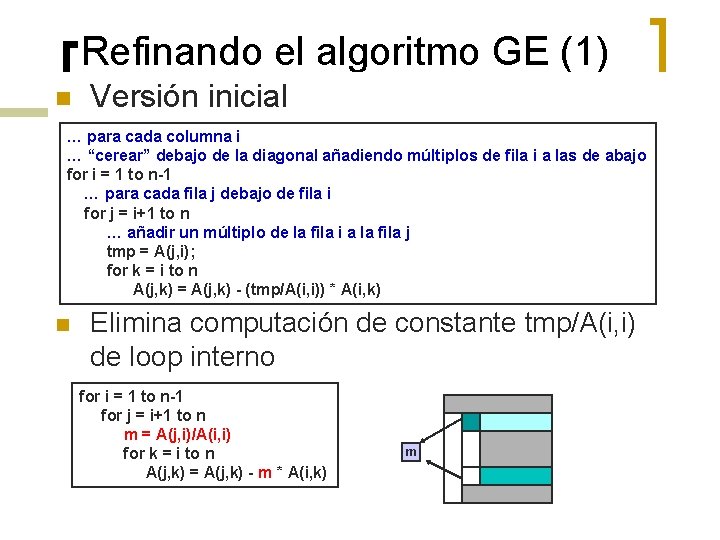
Refinando el algoritmo GE (1) n Versión inicial … para cada columna i … “cerear” debajo de la diagonal añadiendo múltiplos de fila i a las de abajo for i = 1 to n-1 … para cada fila j debajo de fila i for j = i+1 to n … añadir un múltiplo de la fila i a la fila j tmp = A(j, i); for k = i to n A(j, k) = A(j, k) - (tmp/A(i, i)) * A(i, k) n Elimina computación de constante tmp/A(i, i) de loop interno for i = 1 to n-1 for j = i+1 to n m = A(j, i)/A(i, i) for k = i to n A(j, k) = A(j, k) - m * A(i, k) m

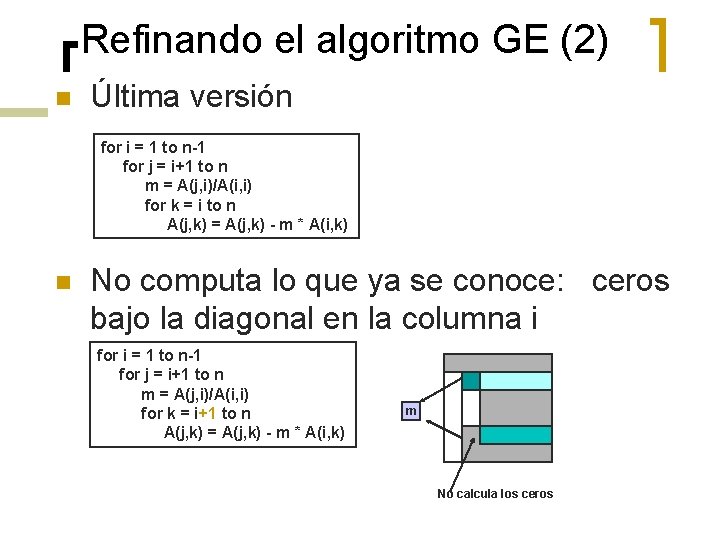
Refinando el algoritmo GE (2) n Última versión for i = 1 to n-1 for j = i+1 to n m = A(j, i)/A(i, i) for k = i to n A(j, k) = A(j, k) - m * A(i, k) n No computa lo que ya se conoce: ceros bajo la diagonal en la columna i for i = 1 to n-1 for j = i+1 to n m = A(j, i)/A(i, i) for k = i+1 to n A(j, k) = A(j, k) - m * A(i, k) m No calcula los ceros

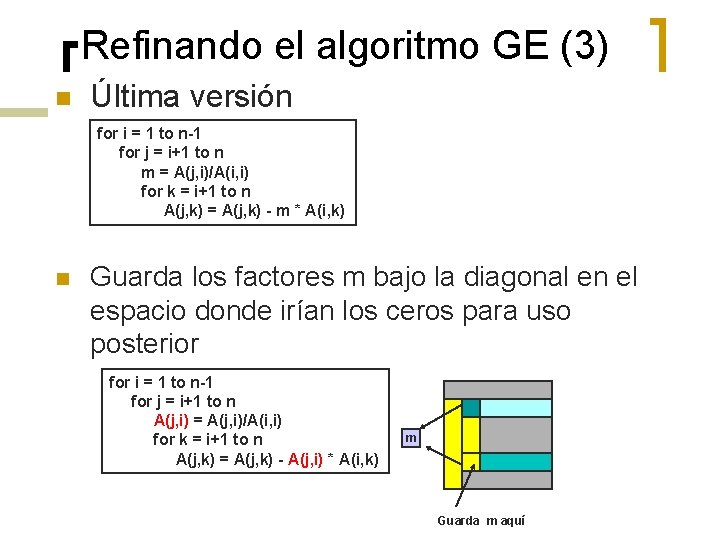
Refinando el algoritmo GE (3) n Última versión for i = 1 to n-1 for j = i+1 to n m = A(j, i)/A(i, i) for k = i+1 to n A(j, k) = A(j, k) - m * A(i, k) n Guarda los factores m bajo la diagonal en el espacio donde irían los ceros para uso posterior for i = 1 to n-1 for j = i+1 to n A(j, i) = A(j, i)/A(i, i) for k = i+1 to n A(j, k) = A(j, k) - A(j, i) * A(i, k) m Guarda m aquí

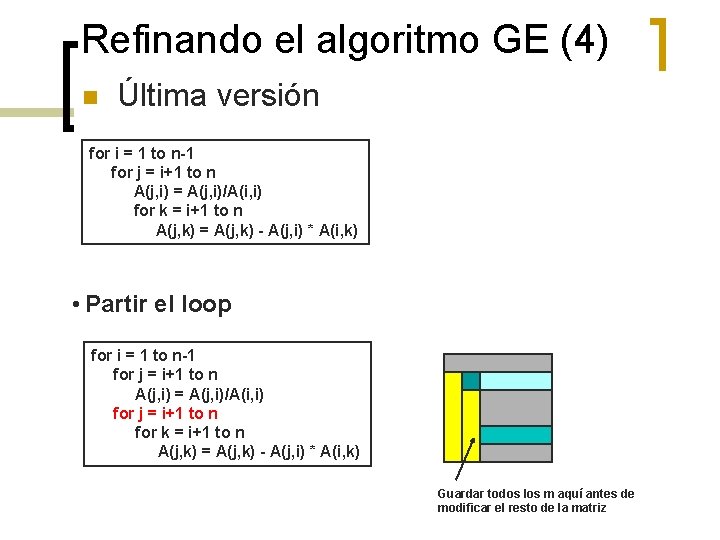
Refinando el algoritmo GE (4) n Última versión for i = 1 to n-1 for j = i+1 to n A(j, i) = A(j, i)/A(i, i) for k = i+1 to n A(j, k) = A(j, k) - A(j, i) * A(i, k) • Partir el loop for i = 1 to n-1 for j = i+1 to n A(j, i) = A(j, i)/A(i, i) for j = i+1 to n for k = i+1 to n A(j, k) = A(j, k) - A(j, i) * A(i, k) Guardar todos los m aquí antes de modificar el resto de la matriz

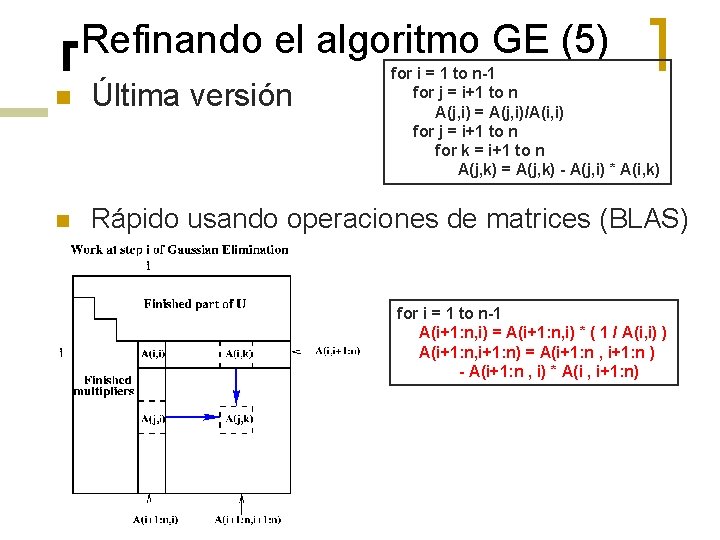
Refinando el algoritmo GE (5) for i = 1 to n-1 for j = i+1 to n A(j, i) = A(j, i)/A(i, i) for j = i+1 to n for k = i+1 to n A(j, k) = A(j, k) - A(j, i) * A(i, k) n Última versión n Rápido usando operaciones de matrices (BLAS) for i = 1 to n-1 A(i+1: n, i) = A(i+1: n, i) * ( 1 / A(i, i) ) A(i+1: n, i+1: n) = A(i+1: n , i+1: n ) - A(i+1: n , i) * A(i , i+1: n)

Qué computa en realidad la GE? for i = 1 to n-1 A(i+1: n, i) = A(i+1: n, i) / A(i, i) A(i+1: n, i+1: n) = A(i+1: n , i+1: n ) - A(i+1: n , i) * A(i , i+1: n) n n Llamemos a la matriz triangular inferior de multiplicadores m como M, y hagamos L = I+M Llamemos al triangulo superior de la matriz final como U Lema (Factorización LU): Si el algoritmo anterior termina (no hay división por cero) entonces A = L*U Solución de A*x=b usando GE ¡ ¡ ¡ n Factorizar A = L*U usando GE (costo = 2/3 n 3 flops) Resolver L*y = b para y, usando substitución (costo = n 2 flops) Resolver U*x = y para x, usando substitución (costo = n 2 flops) Por lo tanto A*x = (L*U)*x = L*(U*x) = L*y = b como se desea

Problemas con el alg. GE básico n Qué pasa si algún A(i, i) es cero? O es muy pequeño? ¡ n Resultado inválido (div. por cero), o “inestable”, se necesita pivotear Se computan operaciones BLAS 1 o BLAS 2, pero sabemos que las BLAS 3 (mult. de matrices) es más rápida (clase anterior…) for i = 1 to n-1 A(i+1: n, i) = A(i+1: n, i) / A(i, i) … BLAS 1 (escala un vector) A(i+1: n, i+1: n) = A(i+1: n , i+1: n ) … BLAS 2 (update en rango 1) - A(i+1: n , i) * A(i , i+1: n) Pico BLAS 3 BLAS 2 BLAS 1
![Pivotear en GE A 0 1 falla por que no Pivotear en GE • A = [ 0 1 ] falla por que no](https://slidetodoc.com/presentation_image_h/cf0f0890660453e410622709fe965395/image-18.jpg)
Pivotear en GE • A = [ 0 1 ] falla por que no se puede dividir entre A(1, 1)=0 [1 0] • Pero resolver Ax=b es facilísimo! • Cuando elemento diagonal A(i, i) es diminuto (no sólo cero), el algoritmo puede terminar pero dar una respuesta completamente errada • Inestabilidad numérica • La causa es el error de redondeo a punto flotante • Cura: usar Pivot (intercambiar filas de A) tal que A(i, i) sea grande

GE con Pivot Parcial (GEPP) • Pivoteo Parcial: intercambiar filas tal que A(i, i) es la mayor en su columna for i = 1 to n-1 Hallar y guardar k donde |A(k, i)| = max{i <= j <= n} |A(j, i)| … o sea, el mayor element en el resto de la columna i if |A(k, i)| = 0 exit con advertencia que A es singular, o casi singular elseif k != i intercambiar filas i , k de A end if A(i+1: n, i) = A(i+1: n, i) / A(i, i) … cada cociente cae en [-1, 1] A(i+1: n, i+1: n) = A(i+1: n , i+1: n ) - A(i+1: n , i) * A(i , i+1: n) • Lema: este algoritmo computa A = P*L*U, donde P es una matriz de permutación. • Es numéricamente estable en la práctica • Para más detalles ver código LAPACK en http: //www. netlib. org/lapack/single/sgetf 2. f

Problemas con el alg. GE básico n Qué pasa si A(i, i) es cero? O es muy pequeño? ¡ n Resultado inválido, o “inestable”, así que se debe pivotear Se computan operaciones BLAS 1 o BLAS 2, pero sabemos que las BLAS 3 (mult. de matrices) es más rápida (clase anterior…) for i = 1 to n-1 A(i+1: n, i) = A(i+1: n, i) / A(i, i) … BLAS 1 (escala un vector) A(i+1: n, i+1: n) = A(i+1: n , i+1: n ) … BLAS 2 (update en rango 1) - A(i+1: n , i) * A(i , i+1: n) Pico BLAS 3 BLAS 2 BLAS 1

Convirtiendo BLAS 2 a BLAS 3 en GEPP n Bloques ¡ ¡ n GRAN IDEA: Updates retrasados ¡ ¡ n Salvar varios updates consecutivos BLAS 2 a una “matriz relegada” Aplicar muchos updates simultáneamente en una operación BLAS 2 La misma idea funciona en otras partes del alg. lineal ¡ n Usado para optimizar mult. matrices Más difícil en GE por las dependencias de data en GEPP Quedan preguntas por resolver…. Primer enfoque: necesito escoger un tamaño de bloque b ¡ ¡ ¡ Algoritmo guarda y aplica b updates b debe ser suficientemente pequeño de tal forma que la sub matriz activa consistente en b columnas de A quepa en el cache b debe ser suficientemente grande para que BLAS 3 sea rápido

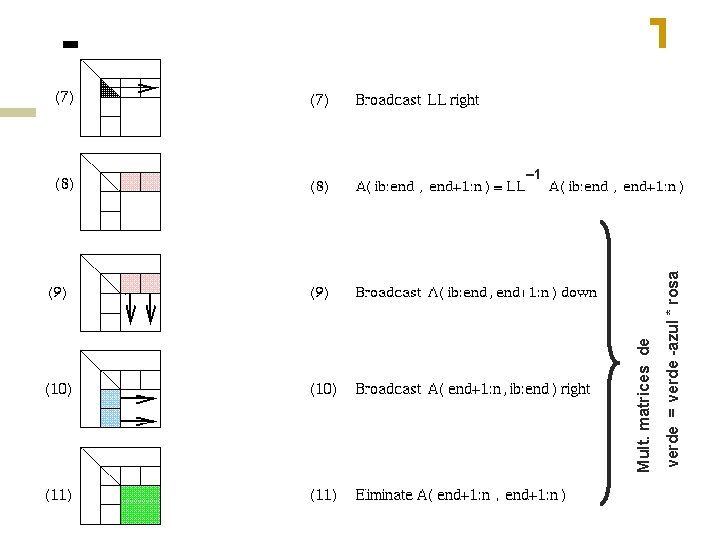
GEPP en bloques (www. netlib. org/lapack/single/sgetrf. f) for ib = 1 to n-1 step b … Procesa b columnas end = ib + b-1 … Apunta al final del bloque de b columns aplica versión BLAS 2 de GEPP para obtener A(ib: n , ib: end) = P’ * L’ * U’ … LL denota la parte triangular inferior de A(ib: end , ib: end) + I A(ib: end , end+1: n) = LL-1 * A(ib: end , end+1: n) … update siguientes b filas de U A(end+1: n , end+1: n ) = A(end+1: n , end+1: n ) - A(end+1: n , ib: end) * A(ib: end , end+1: n) … aplica updates retrasados con una mult. matrices … de dimensiones w x b , b x w

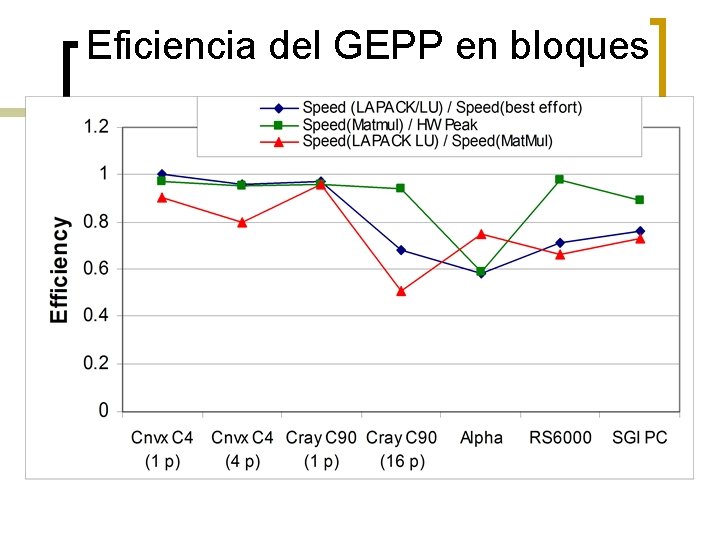
Eficiencia del GEPP en bloques

Vista general de LAPACK y Sca. LAPACK n Librería estándar para algebra lineal densa y en bandas ¡ ¡ n n n Sistemas lineales: A*x=b Problemas de mínimos cuadrados: minx || A*x-b ||2 Problemas de Eigenvalues: Ax = lx, Ax = l. Bx Descomposición en valores singulares (SVD): A = USVT Alg. reorganizados para usar lo más posible BLAS 3 Base de librerías matemáticas en muchos sistemas, Matlab, etc … Aún faltan más mejoras por implementar ¡ Proyectos para maestrías, doctorados?

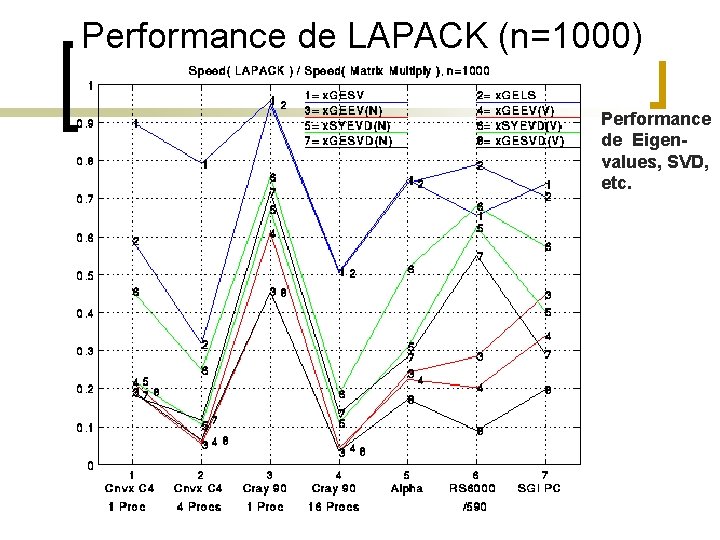
Performance de LAPACK (n=1000) Performance de Eigenvalues, SVD, etc.

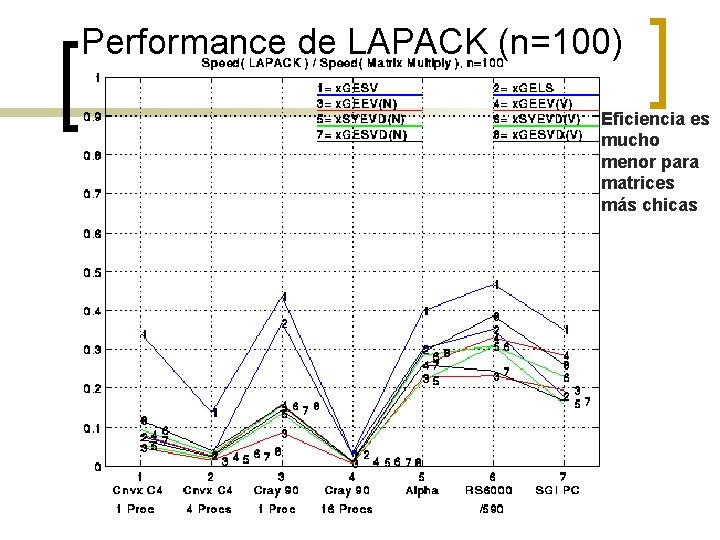
Performance de LAPACK (n=100) Eficiencia es mucho menor para matrices más chicas

Paralelizando la GE n Pasos de la paralelización ¡ ¡ n Descomposición: identificar suficiente trabajo paralelo, pero no demasiado Asignación: balance de carga entre procesos Coordinación: comunicación y sincronización Mapeo: qué procesadores ejecutan qué tareas? Descomposición ¡ En la parte BLAS 2, casi cada flop en el loop interno puede hacerse en paralelo, así que con n 2 procs. , necesito 3 n pasos paralelos for i = 1 to n-1 A(i+1: n, i) = A(i+1: n, i) / A(i, i) … BLAS 1 (escala un vector) A(i+1: n, i+1: n) = A(i+1: n , i+1: n ) … BLAS 2 (update rango 1) - A(i+1: n , i) * A(i , i+1: n) ¡ ¡ n Esto es grano muy fino, mejor es llamar a mult. matrices locales Necesario usar mult. matrices paralelo Asignación ¡ Que procesadores son responsables de qué submatrices?

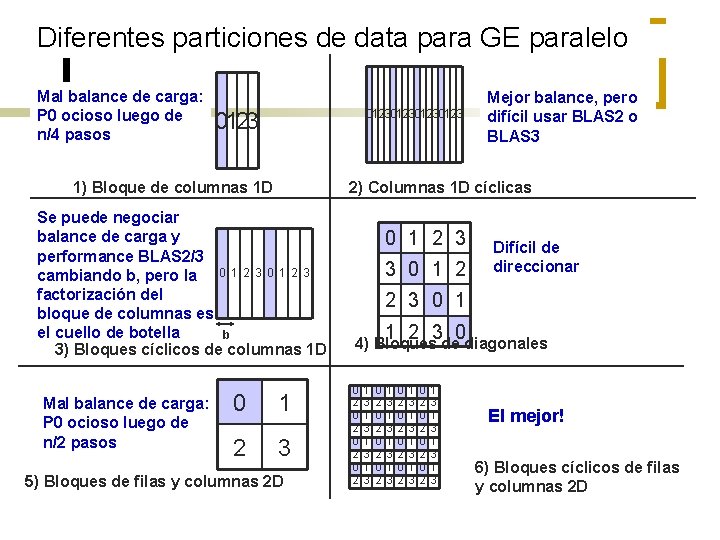
Diferentes particiones de data para GE paralelo Mal balance de carga: P 0 ocioso luego de n/4 pasos 012301230123 1) Bloque de columnas 1 D 2) Columnas 1 D cíclicas Se puede negociar balance de carga y performance BLAS 2/3 cambiando b, pero la 0 1 2 3 factorización del bloque de columnas es el cuello de botella b 3) Bloques cíclicos de columnas 1 D Mal balance de carga: P 0 ocioso luego de n/2 pasos Mejor balance, pero difícil usar BLAS 2 o BLAS 3 0 1 2 3 5) Bloques de filas y columnas 2 D 0 1 2 3 3 0 1 2 Difícil de direccionar 2 3 0 1 1 2 3 0 4) Bloques de diagonales 0 2 0 2 1 3 1 3 0 2 0 2 10 32 1 3 1 3 0 2 0 2 1 3 1 3 El mejor! 6) Bloques cíclicos de filas y columnas 2 D

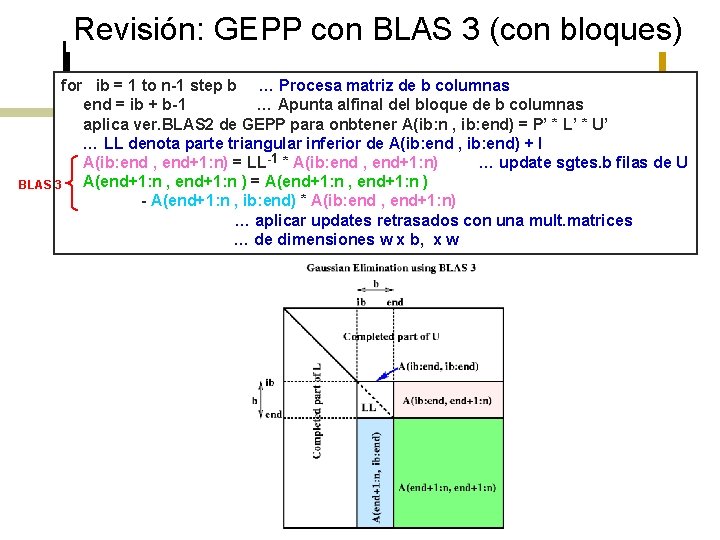
Revisión: GEPP con BLAS 3 (con bloques) for ib = 1 to n-1 step b … Procesa matriz de b columnas end = ib + b-1 … Apunta alfinal del bloque de b columnas aplica ver. BLAS 2 de GEPP para onbtener A(ib: n , ib: end) = P’ * L’ * U’ … LL denota parte triangular inferior de A(ib: end , ib: end) + I A(ib: end , end+1: n) = LL-1 * A(ib: end , end+1: n) … update sgtes. b filas de U A(end+1: n , end+1: n ) = A(end+1: n , end+1: n ) BLAS 3 - A(end+1: n , ib: end) * A(ib: end , end+1: n) … aplicar updates retrasados con una mult. matrices … de dimensiones w x b, x w

Bloque cíclico de Filas y Columnas bcol brow 0 1 0 10 1 0 1 2 3 2 32 3 2 3 • Procesadores y bloques de matrices están distribuidos en un array 2 d • Array de procesadores prow x pcol • Bloques de matrices brow x bcol • Paralelismo “pcol” veces en cualquier columna, y llamadas a BLAS 2 y BLAS 3 en matrices de tamaño brow x bcol • Cuello de botella serial es menos problemático • prow pcol y brow bcol posible, es más deseable

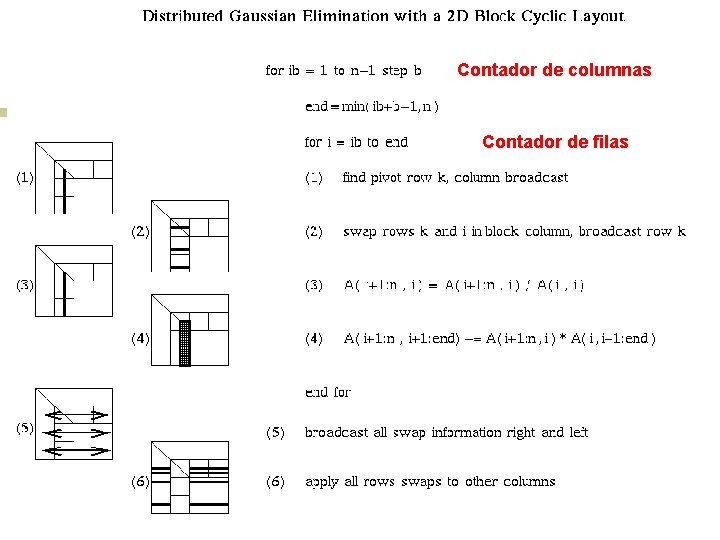
GE distribuido con Bloques cíclicos 2 D • Tamaño de bloque b en el algoritmo y los tamaños de bloque brow y bcol en la partición satisfacen b=bcol. • Regiones sombreadas indican procesadores ocupados con computación o comunicación. • No es necesario tener barrera entre pasos sucesivos del algoritmo, ej: pasos 9, 10, y 11 se pueden hacer en “paralelo”

Distributed GE with a 2 D Block Cyclic Layout Contador de columnas Contador de filas

verde = verde -azul * rosa Mult. matrices de – 1

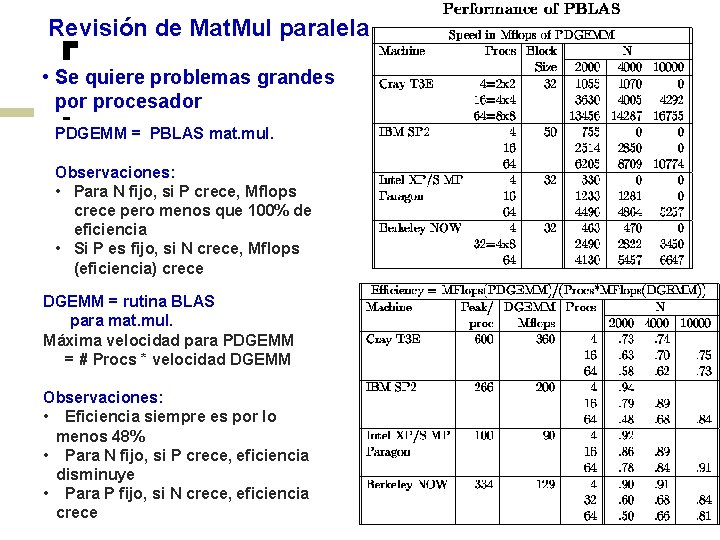
Revisión de Mat. Mul paralela • Se quiere problemas grandes por procesador PDGEMM = PBLAS mat. mul. Observaciones: • Para N fijo, si P crece, Mflops crece pero menos que 100% de eficiencia • Si P es fijo, si N crece, Mflops (eficiencia) crece DGEMM = rutina BLAS para mat. mul. Máxima velocidad para PDGEMM = # Procs * velocidad DGEMM Observaciones: • Eficiencia siempre es por lo menos 48% • Para N fijo, si P crece, eficiencia disminuye • Para P fijo, si N crece, eficiencia crece

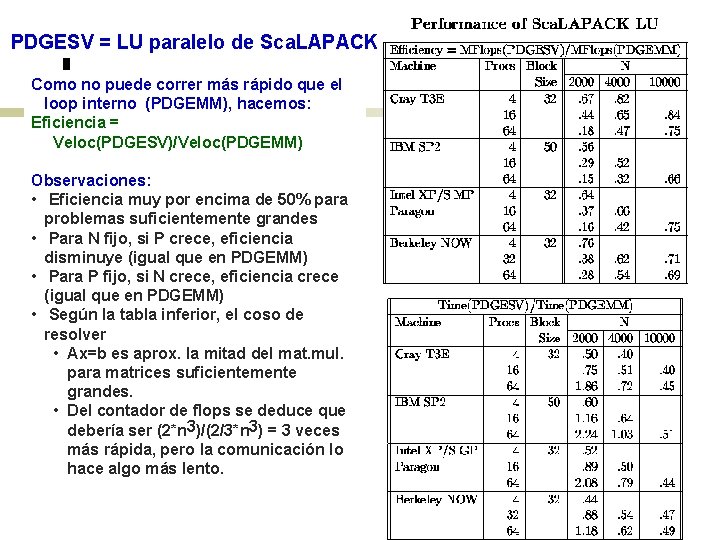
PDGESV = LU paralelo de Sca. LAPACK Como no puede correr más rápido que el loop interno (PDGEMM), hacemos: Eficiencia = Veloc(PDGESV)/Veloc(PDGEMM) Observaciones: • Eficiencia muy por encima de 50% para problemas suficientemente grandes • Para N fijo, si P crece, eficiencia disminuye (igual que en PDGEMM) • Para P fijo, si N crece, eficiencia crece (igual que en PDGEMM) • Según la tabla inferior, el coso de resolver • Ax=b es aprox. la mitad del mat. mul. para matrices suficientemente grandes. • Del contador de flops se deduce que debería ser (2*n 3)/(2/3*n 3) = 3 veces más rápida, pero la comunicación lo hace algo más lento.

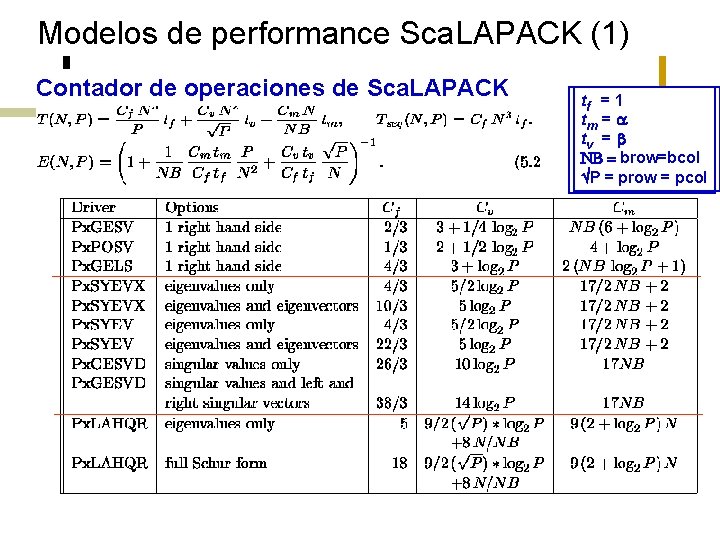
Modelos de performance Sca. LAPACK (1) Contador de operaciones de Sca. LAPACK tf = 1 tm = a tv = b NB = brow=bcol P = prow = pcol

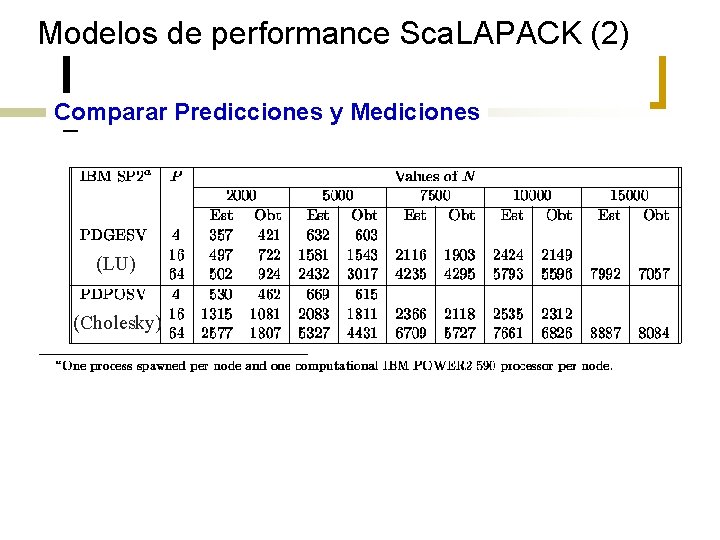
Modelos de performance Sca. LAPACK (2) Comparar Predicciones y Mediciones (LU) (Cholesky)

Escalabilidad de LAPACK y Sca. LAPACK n Problemas “unilaterales” son escalables ¡ ¡ n En GE, A factorizada como el producto de 2 matrices A = LU por medio de pre-multiplicar A por una secuencia de matrices más simples Asintóticamente es 100% BLAS 3 LU (“Linpack Benchmark”) Cholesky, QR Problemas “Bilaterales” som menos escalables ¡ ¡ ¡ A factorizada como producto de 3 matrices por medio de pre y post multiplicación 50% BLAS 2, no llega a 100% BLAS 3 Eigenproblemas, SVD descomposición de valor singular n n Problemas de banda estrecha son los peores (para llevarlo a BLAS 3 o paralelizar) ¡ n Eigenproblemas asimétricos son peores Ecuaciones lineales y eigenproblemas www. netlib. org/{lapack, scalapack}

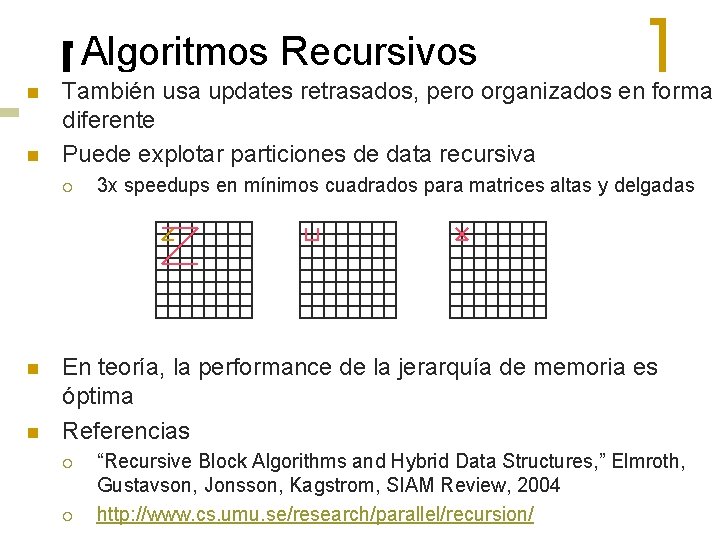
Algoritmos Recursivos n n También usa updates retrasados, pero organizados en forma diferente Puede explotar particiones de data recursiva ¡ n n 3 x speedups en mínimos cuadrados para matrices altas y delgadas En teoría, la performance de la jerarquía de memoria es óptima Referencias ¡ ¡ “Recursive Block Algorithms and Hybrid Data Structures, ” Elmroth, Gustavson, Jonsson, Kagstrom, SIAM Review, 2004 http: //www. cs. umu. se/research/parallel/recursion/

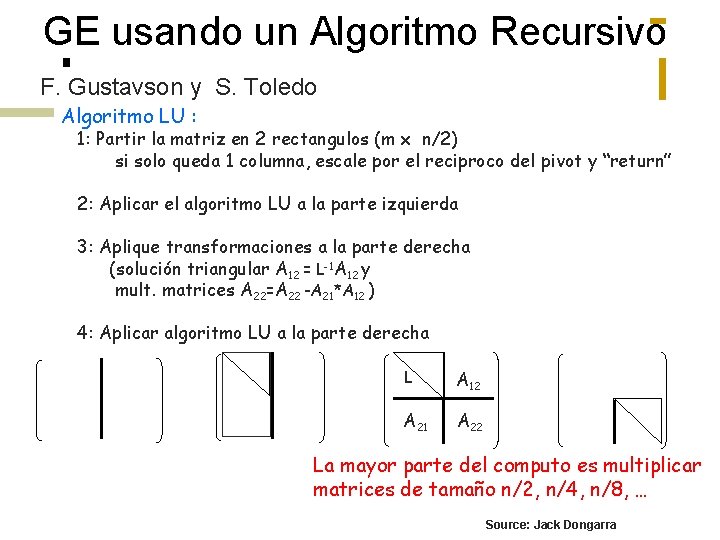
GE usando un Algoritmo Recursivo F. Gustavson y S. Toledo Algoritmo LU : 1: Partir la matriz en 2 rectangulos (m x n/2) si solo queda 1 columna, escale por el reciproco del pivot y “return” 2: Aplicar el algoritmo LU a la parte izquierda 3: Aplique transformaciones a la parte derecha (solución triangular A 12 = L-1 A 12 y mult. matrices A 22=A 22 -A 21*A 12 ) 4: Aplicar algoritmo LU a la parte derecha L A 12 A 21 A 22 La mayor parte del computo es multiplicar matrices de tamaño n/2, n/4, n/8, … Source: Jack Dongarra

Factorizaciones recursivas n n n Tan precisas como los métodos convencionales Mismo número de operaciones Se forman bloques de tamaño variable en forma automática ¡ Sólo operaciones BLAS nivel 1 y 3! Simplicidad de expresión Potencialmente eficientes pero a la vez “indiferente” al caché ¡ n Pero no se debería llevar la recursión hasta el extremo de 1 columna! La formulación recursiva es sólo un reajuste de algoritmos más viejos del LINPACK

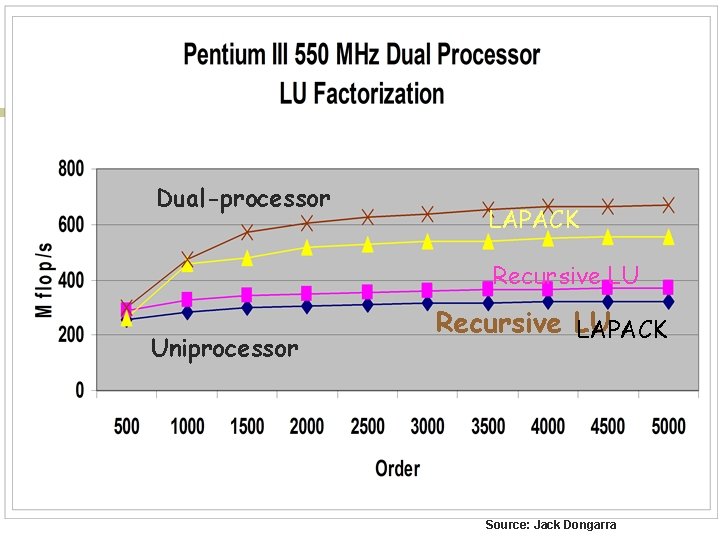
Dual-processor LAPACK Recursive LU Uniprocessor Recursive LU LAPACK Source: Jack Dongarra

Limites de los algortimos recursivos n n Dos clases de descomposiciones de matrices densas “Unilaterales” ¡ ¡ Secuencia de operaciones sencillas aplicadas en la izquierda de la matriz GE: A = L*U o A = P*L*U n n ¡ ¡ ¡ n GE simétrica: A = L*D*LT Cholesky, sólo matrices simétricas: A = L*LT Descomposición QR para mínimos cuadrados: A = Q*R Puede acercarse a 100% BLAS 3 Susceptible de recursión “Bilaterales” ¡ ¡ ¡ Secuencia de operaciones sencillas aplicadas en ambos lados, alternadamente Algoritmos de Eigenvalores, SVD Por lo menos ~25% BLAS 2 Enfoque recursivo imposible, difícil? Algunos progresos la última decada: SVD (25% vs 50% BLAS 2)

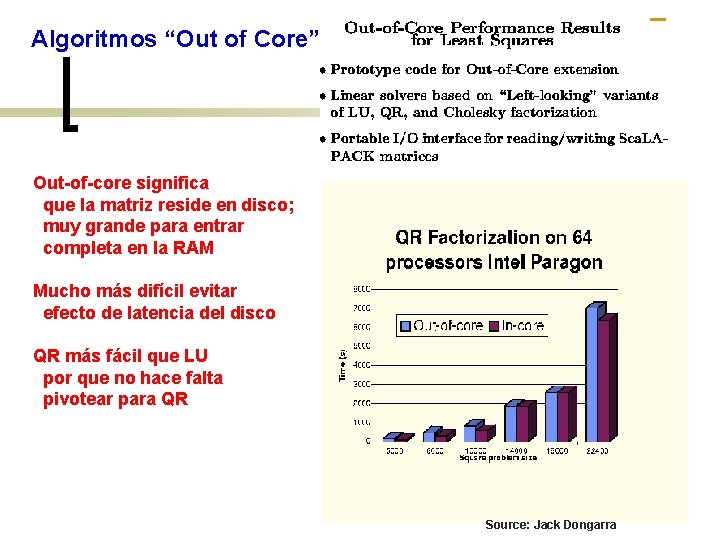
Algoritmos “Out of Core” Out-of-core significa que la matriz reside en disco; muy grande para entrar completa en la RAM Mucho más difícil evitar efecto de latencia del disco QR más fácil que LU por que no hace falta pivotear para QR Source: Jack Dongarra

Resolviendo Sist. Ec. Lineales provenientes de Ec. Dif. Parc.

Repaso de “Fuentes de paralelismo” n Sistemas de eventos discretos: ¡ n Sistemas de partículas: ¡ n Ejs: bolas de billar, simulación de dispositivos semiconductores, galaxias. Variables agregadas dependientes de parámetros continuos: ¡ n Ejs: “Game of Life, ” simulación de circuitos lógicos. EDOs, ejs: simulación de circuitos (Spice), mecánica estructral, cinética química. Variables contínuas dependientes de parámetros continuos: ¡ EDPs, ejs: calor, elasticidad, electrostática.

Repaso: Resolviendo EDPs ° Problemas hiperbólicos (ondas): ¡ Onda sonora (posición, time) ¡ Usan iteración en el tiempo en forma explícita ¡ Solución en cada punto depende de los vecinos en Δt anterior n Problemas elípticos (estado estable): ¡ Potencial electrostático (posición) ¡ Todo valor depende de todos lo demás valores ¡ Localidad es más difícil de hallar que en los problemas hiperbólicos n Problemas parabólicos (dependientes del tiempo): ¡ Temperatura (posición, tiempo) ¡ Involucra una solución elíptica cada Δt n Nos enfocaremos en los elípticos ¡ Ejemplo canónico es la ec. Poisson 2 u/ x 2 + 2 u/ y 2 + 2 u/ z 2 = f(x, y, z)

Ec. Poisson aparece en muchos lados 3 D: 2 u/ x 2 + 2 u/ y 2 + 2 u/ z 2 = f(x, y, z) 2 D: 2 u/ x 2 + 2 u/ y 2 = f(x, y) 1 D: d 2 u/dx 2 = f(x) n n n f representa las fuentes; además se necesita condiciones de frontera Potencial electrostático o gravitacional: Potencial (posición) Flujo de calor: Temperatura (posición, tiempo) Difusión: Concentración (posición, tiempo) Flujo de fluidos: Velocidad, Presión , Densidad (posición, tiempo) Elasticidad: Tensión, estiramiento (posición, tiempo) Variaciones de Poisson tienen coeficientes variables

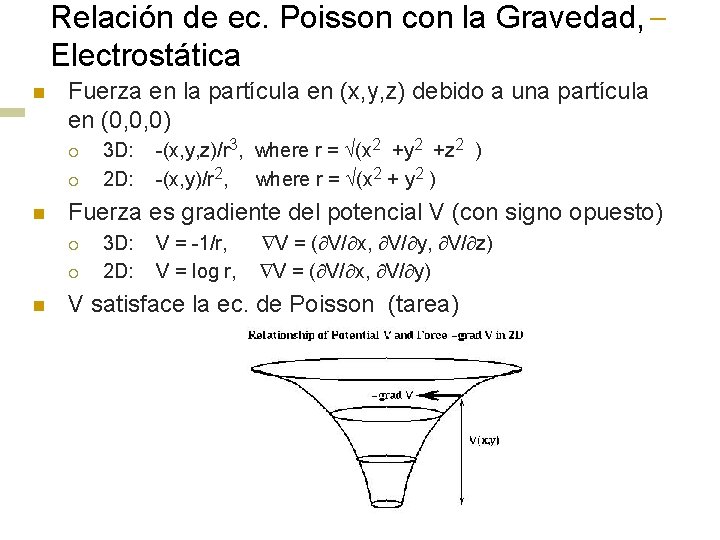
Relación de ec. Poisson con la Gravedad, Electrostática n Fuerza en la partícula en (x, y, z) debido a una partícula en (0, 0, 0) ¡ ¡ n -(x, y, z)/r 3, where r = (x 2 +y 2 +z 2 ) -(x, y)/r 2, where r = (x 2 + y 2 ) Fuerza es gradiente del potencial V (con signo opuesto) ¡ ¡ n 3 D: 2 D: V = -1/r, V = log r, V = ( V/ x, V/ y, V/ z) V = ( V/ x, V/ y) V satisface la ec. de Poisson (tarea)

Ec. Poisson en 1 D: 2 u/ x 2 = f(x) Discretizar d 2 u/dx 2 = f(x) en la malla regular ui = u(i*h) Para conseguir [ u i+1 – 2*u i + u i-1 ] / h 2 = f(x) Se resuelve como Tu = -h 2 * f Para array desconocido u donde T= 2 -1 -1 2 Grafo y “estencil” -1 2 -1

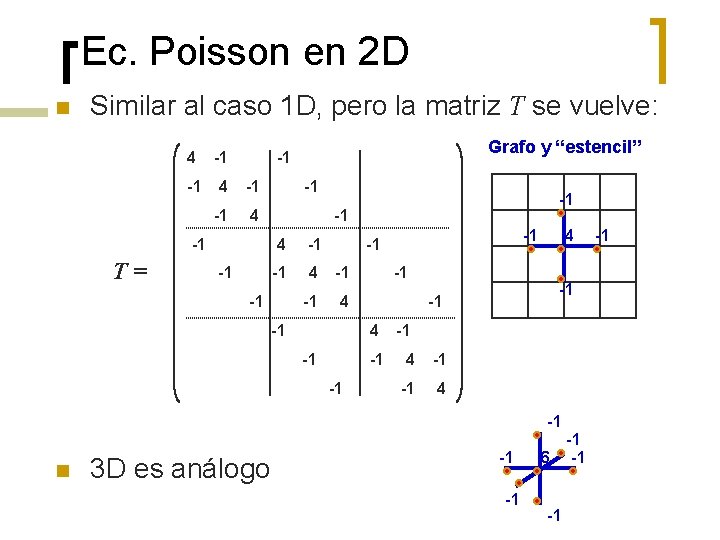
Ec. Poisson en 2 D n Similar al caso 1 D, pero la matriz T se vuelve: 4 -1 -1 4 -1 T= Grafo y “estencil” -1 -1 -1 4 -1 -1 -1 4 -1 n 3 D es análogo -1 -1 6 -1 -1

Algoritmos para Poisson 2 D (3 D) (N = n 2 (n 3) vars) Algoritmo Serial n LU denso N 3 n LU bandas N 2 (N 7/3) n Jacobi N 2 (N 5/3) n Inv. Explicit N 2 n Gradiente Conj. N 3/2 (N 4/3) n SOR r/n N 3/2 (N 4/3) n LU dispersa N 3/2 (N 2) n FFT N*log N n Multigrid N n MINIMO N PRAM N N N (N 2/3) log N N 1/2(1/3) *log N N 1/2 (N 1/3) N 1/2 log N log 2 N log N Memoria N 2 N 3/2 (N 5/3) N N 2 N N N*log N (N 4/3) N N N #Procs N 2 N (N 4/3) N N 2 N N N PRAM es un modelo de paralelismo ideal con costo de comunicación despreciable Referencia: James Demmel, Applied Numerical Linear Algebra, SIAM, 1997.

Resumen de Algoritmos en malla n x n grid (n x n) (1) n. El orden de presentación es así (aprox. ): ¡ Del más lento al más rápido en máquinas secuenciales. ¡ Del más general (trabaja en cualquier matriz) al más especializado (trabaj en matrices “parecidas” a T). n. LU denso: GE; trabaja en cualquier matriz N-by-N. n. LU en bandas: aprovecha el hecho que T es ≠ de cero solo en las N 1/2 (N 2/3) diagonales más cercanas a la diagonal principal. n. Jacobi: básicamente hace mult. matriz vector por T en el loop interno de un algoritmo iterativo. n. Inverso explícito: Asume queremos resolver muchos problemas con la misma T, así que se precalcula y guarda inv(T) “gratis”, y se multiplica por ella (pero todavía caro!). n. Gradiente conjugada: usa mult. matriz vector, como Jacobi, pero aprovecha propiedades matemáticas de T que Jacobi no aprovecha. n. SOR (successive over-relaxation) rojo/negro: Variación de Jacobi que explota otras propiedades de T. Usado en multigrid. n. LU disperso: GE explotando la estructura particular de ceros de T. n. FFT (fast Fourier transform): Trabaja sólo en matrices muy similares a T. n. Multigrid: trabaja en matrices similares a T, que vienen de ec. elípticas. n. MINIMO: estadística del mejor Serial (tiempo para tener la respuesta en output); del mejor paralelo (tiempo para combinar los N outputs).

Resumen de Algoritmos en malla n x n grid (n x n) (2) n. Dimensión = N = n 2 en 2 D (=n 3 en 3 D) n. Ancho de banda = BW = n en 2 D (=n 2 en 3 D) n. Número de Condición= k = n 2 en 2 D ó 3 D n#its = número de iteraciones n. Sp. MV = Sparse-matrix-vector-multiply n. LU densa: ¡ costo n. LU = N 3 (serial) ó N (paralelo, con N 2 procs) en bandas: ¡ costo = N * BW 2 (serial) ó N (paralelo con BW 2 procs) n. Jacobi: ¡ costo = costo(Sp. MV) * #its, #its = k. n. Gradiente ¡ costo n. SOR conjugada: = (costo(Sp. MV) + costo(prod vectorial))* #its, #its = sqrt(k) roja/negra: ¡ costo = costo(Sp. MV) * #its, #its = sqrt(k) n. Algoritmos Iterativos necesitan diversos supuestos para análisis de convergencia

Comentarios en mallas en la práctica n Mallas regulares 1 D, 2 D, 3 D ¡ ¡ n Importantes como bloques básicos para fromar mallas más complicadas Se discutirán primero Mallas en la prácticas son irregular con frecuencia ¡ ¡ ¡ Mallas compuestas, consistentes de vrias mallas regulares “torcidas” unidas en los bordes Mallas no estructuradas, Con puntos de malla y coneccones arbitrarias Mallas adaptativas, cambian en resolución (tamaño, finura) a lo largo del proceso de solución para computar más donde se necesita más precisión

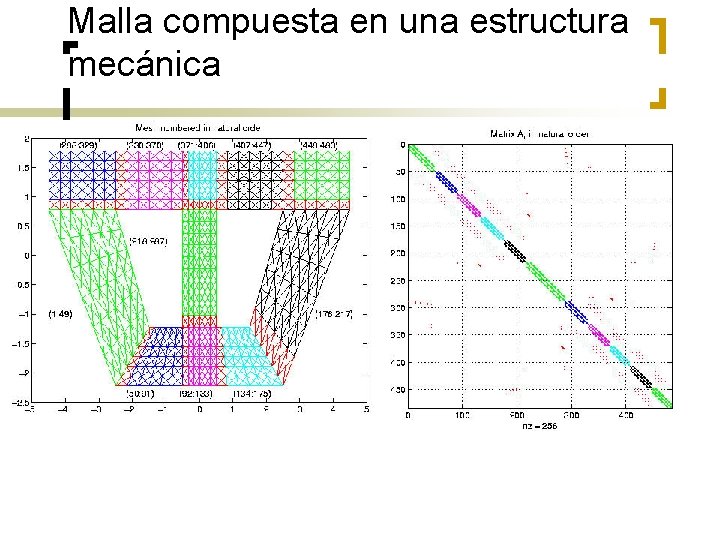
Malla compuesta en una estructura mecánica

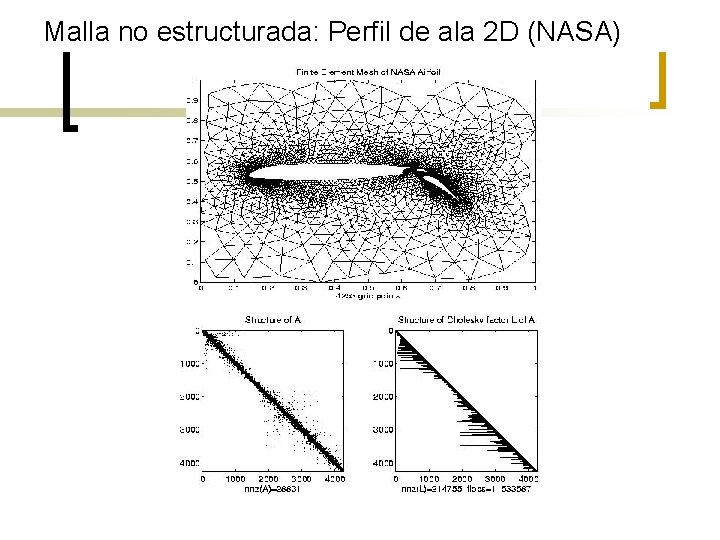
Malla no estructurada: Perfil de ala 2 D (NASA)

Refinamiento de malla adaptativa (AMR) °Malla adaptativa alrededor de una explosión °Fuente: John Bell y Phil Colella en LBL

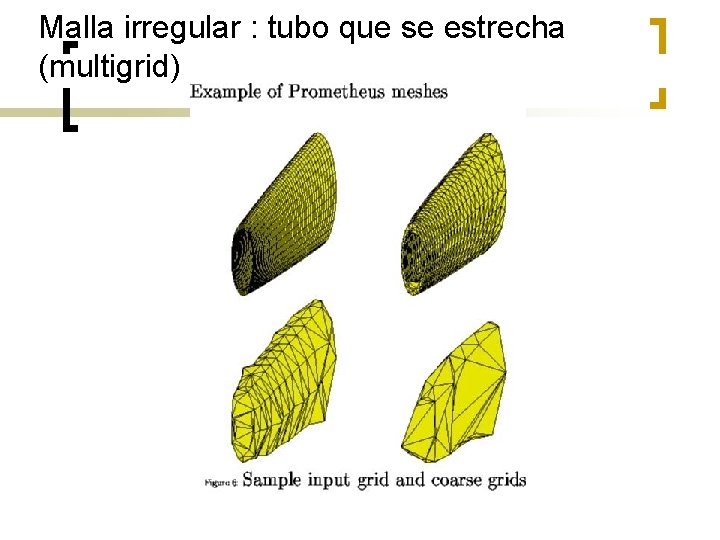
Malla irregular : tubo que se estrecha (multigrid)

Método de Jacobi Para derivar este método, escribir Poisson como: u(i, j) = (u(i-1, j) + u(i+1, j) + u(i, j-1) + u(i, j+1) + b(i, j))/4 n Hacer u(i, j, m) la aproximación de u(i, j) después de m pasos u(i, j, m+1) = (u(i-1, j, m) + u(i+1, j, m) + u(i, j-1, m) + u(i, j+1, m) + b(i, j)) / 4 n O sea, u(i, j, m+1) es un promedio ponderado de vecinos n Motivación: u(i, j, m+1) escogido para satisfacer exactamente la ecuación en el punto (i, j) n Pasos para converger proporcional al tamaño del problema, N=n 2 n ¡ n Ver Lección 24 de www. cs. berkeley. edu/~demmel/cs 267_Spr 99 Por lo tanto, complejidad serial es de O(N 2)

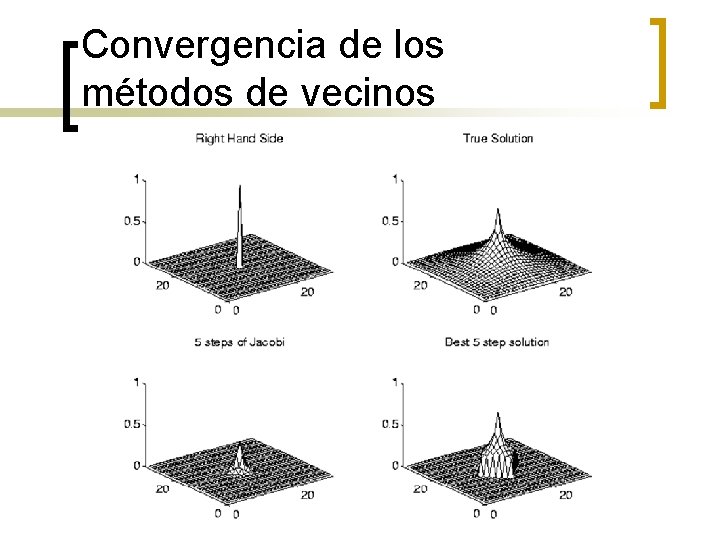
Convergencia de los métodos de vecinos n Jacobi involucra la computación de los vecinos más próximos en una malla nxn (N = n 2) ¡ n n Así que toma O(n) = O(sqrt(N)) iteraciones para que la información se propague Ej. , considerar un vector b = 0, excepto en el centro =1 La solución exacta es más o menos así: Aún en el mejor caso, cualquier computación de vecinos más próximos toma n/2 pasos para propagarse en una malla nxn

Convergencia de los métodos de vecinos

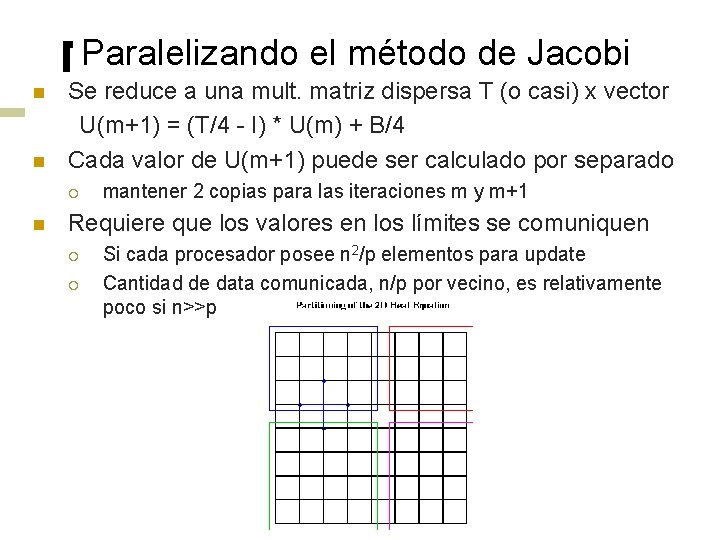
Paralelizando el método de Jacobi n n Se reduce a una mult. matriz dispersa T (o casi) x vector U(m+1) = (T/4 - I) * U(m) + B/4 Cada valor de U(m+1) puede ser calculado por separado ¡ n mantener 2 copias para las iteraciones m y m+1 Requiere que los valores en los límites se comuniquen ¡ ¡ Si cada procesador posee n 2/p elementos para update Cantidad de data comunicada, n/p por vecino, es relativamente poco si n>>p

Optimización de Localidad en Jacobi n Update de vecinos más próximos en Jacobi tiene: ¡ ¡ Buena localidad espacial (en mallas regulares): fila / columna Mala localidad temporal: pocos flops por punto n n Ej: en mallas 2 D: 4 sumas y 1 mult. vs. 5 lecturas y 1 escritura Para proc. Paralelo o secuencial, se puede reducir ops. memoria por un aumento de cómputos ¡ ¡ ¡ Idea: para cada submalla, hacer varias iteraciones de Jacobi Tamaño de submalla se achica con cada iteración, así que comenzar con la mayor Usado en uniprocesadores: n Rescheduling para Localidad, Michelle Mills Strout: ¡ n ¡ www-unix. mcs. anl. gov/~mstrout Algoritmos multigrid eficientes en uso de cache, Sid Chatterjee Y comput. paralelas, incluyendo “ajustes” de mallas n Ian Foster et al, SC 2001

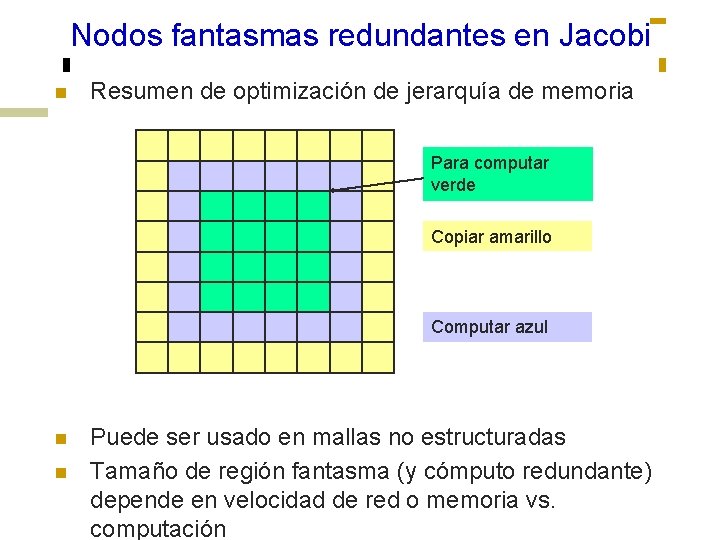
Nodos fantasmas redundantes en Jacobi n Resumen de optimización de jerarquía de memoria Para computar verde Copiar amarillo Computar azul n n Puede ser usado en mallas no estructuradas Tamaño de región fantasma (y cómputo redundante) depende en velocidad de red o memoria vs. computación

Sobre-Relajación Sucesiva (SOR) n n n Similar a Jacobi: u(i, j, m+1) se calcula como una combinación lineal de los vecinos Coefic. numéricos y orden de updates son diferentes Basado en 2 mejoras respecto a Jacobi ¡ ¡ n Usa los “valores más recientes” disponible para u, por que estos valores posiblemente son más precisos Gauss Seidel Actualizar el valor de u(m+1) “más agresivamente” a cada paso Primero, note que cuando evaluamos secuencialmente ¡ u(i, j, m+1) = (u(i-1, j, m) + u(i+1, j, m) … algunos de los valores para m+1 ya están disponibles ¡ u(i, j, m+1) = (u(i-1, j, latest) + u(i+1, j, latest) … donde “latest” es ya sea m ó m+1

Gauss-Seidel n Actualizar de izq. -a-der. en orden por filas, es el algoritmo de Gauss-Seidel for i = 1 to n for j = 1 to n u(i, j, m+1) = (u(i-1, j, m+1) + u(i+1, j, m) + u(i, j-1, m+1) + u(i, j+1, m) + b(i, j)) / 4 n No puede paralelizarse, debido a las dependencias, así que mejor se usa el orden “rojo-negro” forall puntos negros u(i, j) u(i, j, m+1) = (u(i-1, j, m) + … forall puntos rojos u(i, j) u(i, j, m+1) = (u(i-1, j, m+1) + … ° Para un gráfico general, usar coloreo de grafos ° Se puede usar conjuntos independ. máximos repetidos para colorear ° Grafo(T) es bipartito => 2 colores (rojo y negro) ° Nodos para cada color pueden ser actualizados simultáneamente ° Sigue siendo multip. vector matriz dispersa, usando submatrices

Sobre-Relajación Sucesiva (SOR) n n n Este Gauss-Seidel rojo-negro converge dos veces más rápido que Jacobi, pero hay el doble de pasos paralelos, así que es lo mismo en la práctica. Para motivar la siguiente mejora, que el paso básico sea: u(i, j, m+1) = u(i, j, m) + corrección(i, j, m) Si la “corrección” es una buena dirección a donde moverse, entonces uno debería moverse aún más lejos en esa diección por un factor w>1 u(i, j, m+1) = u(i, j, m) + w * correction(i, j, m) Se le llama “successive overrelaxation” (SOR) Paraleliza como Jacobi (Multip. vector matriz dispersa…) Se puede probar que w = 2/(1+sin(p/(n+1)) ) da mejor convergencia ¡ ¡ Número de pasos para converger = complejidad paralela = O(n), en vez del O(n 2) de Jacobi Complejidad Serial O(n 3) = O(N 3/2), en vez del O(n 4) = O(N 2) de Jacobi

Gradiente Conjugada (CG) para resolver A*x = b n Este método puede usarse cuando la matriz A es ¡ ¡ simétrica, o sea, A = AT positiva definida, o sea cualquiera de estas 3 definiciones equivalentes: n n El algoritmo mantiene 3 vectores ¡ ¡ ¡ n x = la solución aproximada, mejorada tras cada iteración r = el residual, r = A*x - b p = dirección de búsqueda, o la gradiente conjugada Costo de una iteración ¡ ¡ n Todos los eigenvalores son positivos x. T * A * x > 0 para todo vector x diferente de 0 Tiene una factorización Cholesky A = L*LT Mult. vector x matriz dispersa A (costo más importante) 3 productos vectoriales, 3 saxpy (escala*vector + vector) Converge en O(n) = O(N 1/2) pasos, como SOR ¡ ¡ Complejidad serial = O(N 3/2) Complejidad paralela = O(N 1/2 log N), factor log N del producto vectorial

Gradiente Conjugada (CG) para resolver A*x = b n n n Aproximación inicial x (“initial guess”, adivinada) r = b – A*x, j=1 Repetir ¡ ¡ ¡ ¡ n rho = r. T*r … producto vectorial If j=1, p = r, else beta = rho/viejo_rho, p = r + beta*p, endif … saxpy q = A*p … Mat. Mul dispersa alpha = rho / p. T * q … producto vectorial x = x + alpha * p … saxpy r = r – alpha * q … saxpy viejo_rho = rho; j=j+1 Hasta que rho sea lo suficientemente pequeño

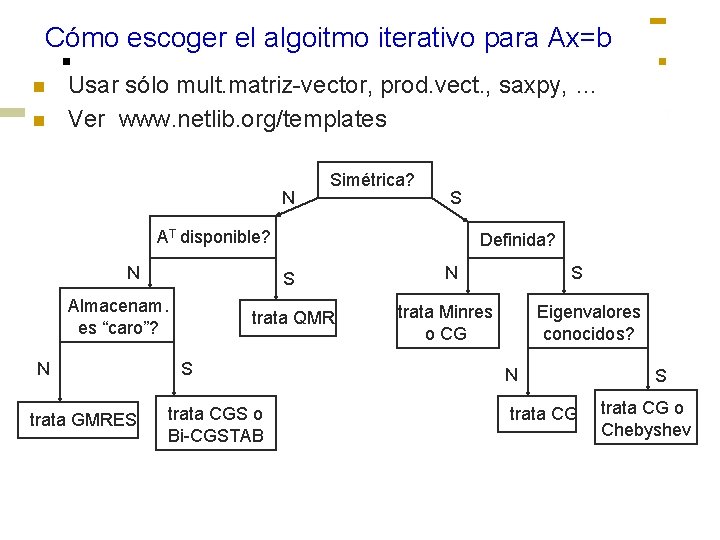
Cómo escoger el algoitmo iterativo para Ax=b n n Usar sólo mult. matriz-vector, prod. vect. , saxpy, … Ver www. netlib. org/templates N Simétrica? S AT disponible? N S Almacenam. es “caro”? N trata GMRES Definida? trata QMR S trata CGS o Bi-CGSTAB N S trata Minres o CG Eigenvalores conocidos? N trata CG S trata CG o Chebyshev

Sumario de Jacobi, SOR y CG n n Todos (Jacobi, SOR, y CG) hacen mult. Matriz dispersa x vector Para Poisson, esto significa comunicación entre vecinos más próximos en una malla n-by-n grid Toma n = N 1/2 pasos para que la información viaje a lo largo de una malla n-por-n Como la solución en un lado de la malla depende de la data en el otro lado de la malla, se necesitan métodos que muevan la información más rápidos ¡ ¡ FFT Multigrid

Resolviendo la Ec. Poisson con FFT n Motivación: expresar la solución continua como serie de Fourier n u(x, y) = Si Sk uik sen(p ix) sen(p ky) ¡ uik es el coeficiente de Fourier de u(x, y) La ecuación de Poisson 2 u/ x 2 + 2 u/ y 2 = b se convierte en: ¡ Si Sk (-pi 2 - pk 2) uik sen(p ix) sen(p ky) = Si Sk bik sen(p ix) sen(p ky) donde bik son los coefic. de Fourier de b(x, y) ° n n Unicidad: como la serie de Fourier es única, uik = bik / (-pi 2 - pk 2) Algoritmo continuo (Algoritmo discreto) ° Computa coefic. Fourier bik del lado derecho de la ecuación ° ° Computa coefic. Fourier uik de la solución ° ° Aplicar FFT 2 D a los valores b(i, k) en la malla Divida cada transformada b(i, k) entre la función(i, k) Computa la solución u(x, y) usando los coef. Fourier ° Aplicar la FFT inversa 2 D a los valores de b(i, k) divididos

FFT Serial Hacer i=sqrt(-1) y que los índices de matrices y vectores empiezen en 0. n La Transformada discreta de Fourier de un vector v de m elementos es: F*v Donde F es la matriz m*m definida como: F[j, k] = v (j*k) Donde v es: v = e (2 pi/m) = cos(2 p/m) + i*sen(2 p/m) v es un número complejo cuyo m-esima potencia vm =1 y por ello es una raiz m-esima de la unidad n Ej. , for m = 4: v = i, v 2 = -1, v 3 = -i, v 4 = 1, n

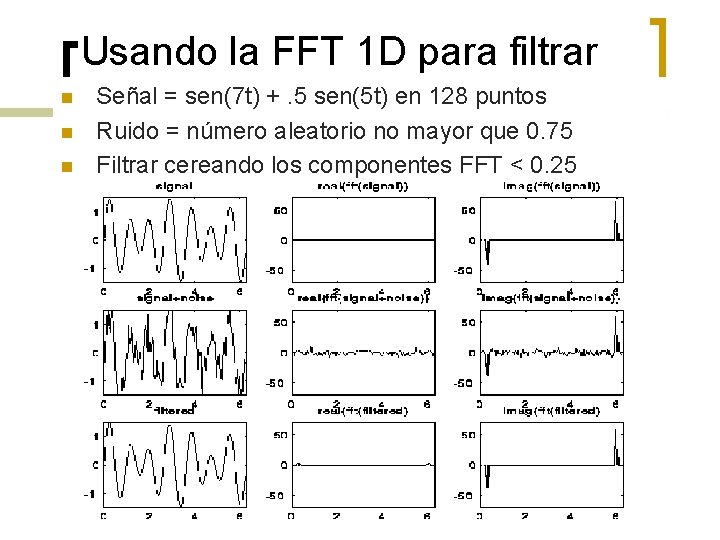
Usando la FFT 1 D para filtrar n n n Señal = sen(7 t) +. 5 sen(5 t) en 128 puntos Ruido = número aleatorio no mayor que 0. 75 Filtrar cereando los componentes FFT < 0. 25

Usando la FFT 2 D para compresión de imágenes n n n Imagen = matriz 200 x 320 pixels (valores) Comprimido manteniendo el 2. 5% más significativo de los componente del FFT, descarta el resto. Similar idea usada en formato jpeg (transf. del coseno)

Transformadas relacionadas n La mayor parte de aplicaciones necesitan multiplicar por F y por la inversa de F. n Multiplicando por F y inversa(F) es esencialmente lo mismo (inversa(F) es la conjugada compleja de F dividida por n) n Para resolver la ec. Poisson y varias otras, usaremos las variaciones de la FFT ¡ ¡ n La transformada del seno – parte imaginaria de F La transformada del coseno – parte real de F Algoritmos similares, así que nos enfocaremos en la “forward FFT”

Algoritmo serial para la FFT n Computar la FFT de un vector v con m elementos, F*v (F*v)[j] = S k = 0 F(j, k) * v(k) m-1 = S k = 0 v (j*k) * v(k) m-1 = S k = 0 (v j)k * v(k) n = V(v j) Donde V es el polinomio m-1 V(x) = Sk = 0 xk * v(k)

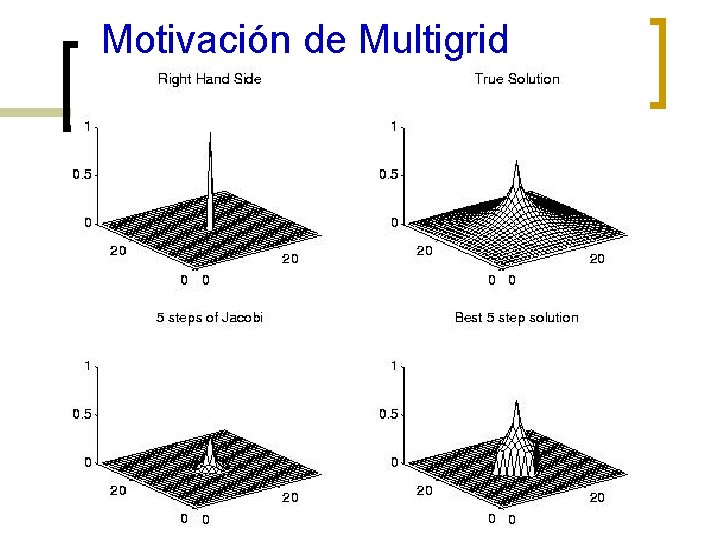
Motivación del Multigrid n Recordemos que Jacobi, SOR, CG, y cualquier otro algoritmo basado en multiplicación de vector por matriz dispersa puede mover información sólo en una celda a la vez (por iteración) ¡ n Se puede mostrar que disminuir el error por un factor fijo c<1 toma mínimo unos W(log n) pasos límite asintótico mínimo ¡ n Mover la información a lo largo de una malla n x n toma por lo menos n pasos Convergencia a un error fijo < 1 toma W(log n ) pasos Por lo tanto, converger en O(1) pasos (número constante de pasos para cualquier n) implica mover información a lo largo de la malla o grilla más rápido que una celda por paso

Motivación de Multigrid

Bases de Multigrid n Algoritmo básico: ¡ ¡ ¡ n Reemplazar problema en una grilla o malla fina por una aproximación en una malla más gruesa (o malla burda) Resolver aproximadamente el problema en la grilla gruesa, y usar la solución como una “starting guess” para el problema en malla fina, el cual es luego resuelto iterativamente Resolver el problema en malla gruesa recursivamente, o sea, usando una aproximación más burda todavía, etc. El éxito depende de que la solución en malla burda sea una buena aproximación a la solución de malla fina

Esa misma Gran Idea se usa en otros lados n n Reemplazar el problema fino por una aproximación burda en forma recursiva. Multilevel Graph Partitioning (METIS): ¡ ¡ n Barnes-Hut (y el método de Multipolo Rápido) para computar las fuerzas gravitacionales de n partículas en tiempo O(n log n): ¡ ¡ n Reemplazar el grafo a ser particionado por un grafo más burdo, obtenido por el “Maximal Independent Set” Dada la partición de la grilla burda, refinar usando Kernighan-Lin Aproximar partículas encajas por masa total, centro de gravedad Suficientemente bueno para partículas lejanas; para las cercanas, dividir la caja en forma recursiva. Todos estos ejemplos dependen de que la aproximación burda sea suficientemente buena (por lo menos si estamos lejos en la recursión)

Multigrid usa “Divide y Vencerás” en 2 formas n 1 ra forma: ¡ n Resolver el problema en una malla dada invocando al Multigrid en una aproximación burda para conseguir una buena “initial guess” a ser refinada después. 2 da forma: ¡ ¡ ¡ Piense que el error es la suma de senos de diferente frecuencias. La misma idea que con el método de las FFT, pero no en forma explícita. Cada llamada al Multgrid es responsable de suprimir los coeficientes de los senos en el 50% de las frecuencias más bajas en el error (gráficos después)

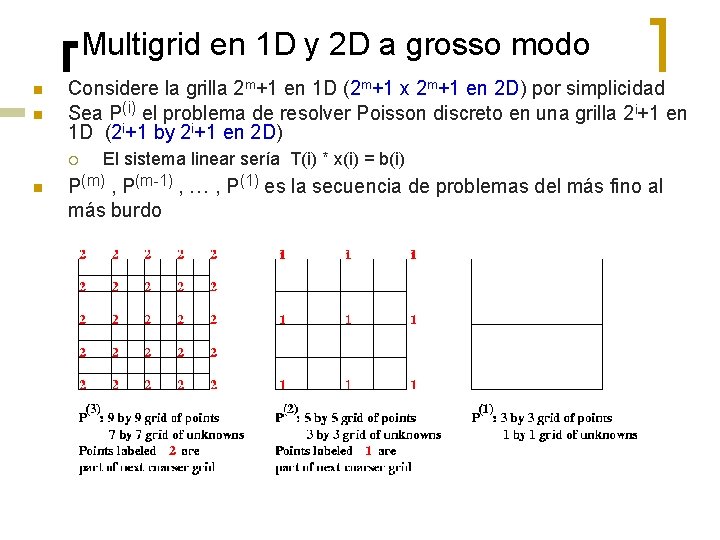
Multigrid en 1 D a grosso modo n n n Considere una grilla 1 D de tamaño 2 m+1 por simplicidad Sea P(i) el problema de resolver la ec. discreta de Poisson en una grilla 2 i+1 en 1 D. La ec. linear sería T(i) * x(i) = b(i) P(m) , P(m-1) , … , P(1) es la secuencia de problemas del más fino al más burdo

Multigrid en 1 D y 2 D a grosso modo n n Considere la grilla 2 m+1 en 1 D (2 m+1 x 2 m+1 en 2 D) por simplicidad Sea P(i) el problema de resolver Poisson discreto en una grilla 2 i+1 en 1 D (2 i+1 by 2 i+1 en 2 D) ¡ n El sistema linear sería T(i) * x(i) = b(i) P(m) , P(m-1) , … , P(1) es la secuencia de problemas del más fino al más burdo

Operadores Multigrid n Para el problema P(i) : ¡ ¡ n n ¡ ¡ Redefine el problema en la grilla fina P(i) a la grilla burda P(i-1) Usa muestreo o promedios b(i-1)= R<i> (b(i)) El operador interpolación In<i-1> mapea la solución aprox. x(i-1) a x(i) ¡ ¡ n Ambos en la grilla de tamaño 2 i-1 Todos los sgtes. operadores solo promedian valores en puntos aledaños en la grilla (así la info se mueve más rápido en mallas burdas) El operador restricción R<i> mapea P(i) a P(i-1) ¡ n b(i) es el vector del lado derecho de la ecuación lineal y x(i) es la solución estimada actualmente Interpola la solución en la malla burda P(i-1) a la fina P(i) x(i) = In<i-1>(x(i-1)) El operador solución S(i) toma P(i) y mejora la solución x(i) ¡ ¡ Usa Jacobi “ponderado” o SOR en un solo nivel de la malla x mejorado (i) = S<i> (b(i), x(i))

Algoritmo Multigrid de ciclo V Function MGV ( b(i), x(i) ) … Resuelve T(i)*x(i) = b(i) dado un b(i) y un “initial guess” para x(i) … retorna un x(i) mejorado if (i = 1) computar solución exacta de x(1) of P(1) solo 1 incógnita return x(1) else x(i) = S<i> (b(i), x(i)) mejorar la solución atenuando el error de alta frecuencia r(i) = T(i)*x(i) - b(i) computar el residual d(i) = In<i-1> ( MGV( R<i> (r(i)), 0 ) ) resolver T(i)*d(i) = r(i) recursivamente x(i) = x(i) - d(i) corregir solución en grilla fina x(i) = S<i> ( b(i), x(i) ) mejorar solución de nuevo return x(i)

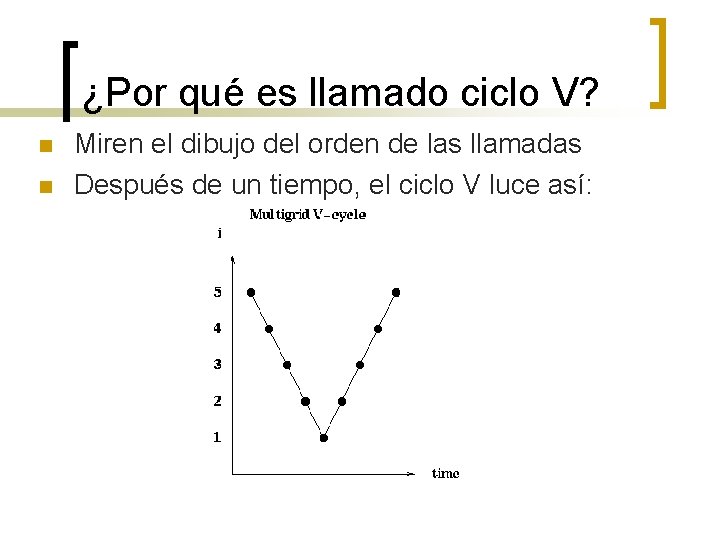
¿Por qué es llamado ciclo V? n n Miren el dibujo del orden de las llamadas Después de un tiempo, el ciclo V luce así:

Complejidad de un Ciclo V n En una computadora serial ¡ ¡ n En cada punto del Ciclo V, el cómputo es del orden O(número de incógnitas) Costo del nivel i-esimo es (2 i-1)2 = O(4 i) Si el nivel m más fino es el m, el tiempo total es: S i=1 O(4 i) = O( 4 m) = O(# incógnitas) En un sistema paralelo (PRAM) ¡ ¡ Con un procesador por cada punto de la grilla y comunicación costo despreciable, cada paso del ciclo V tarda un tiempo constante Tiempo Total del ciclo V es O(m) = O(log #incógnitas)

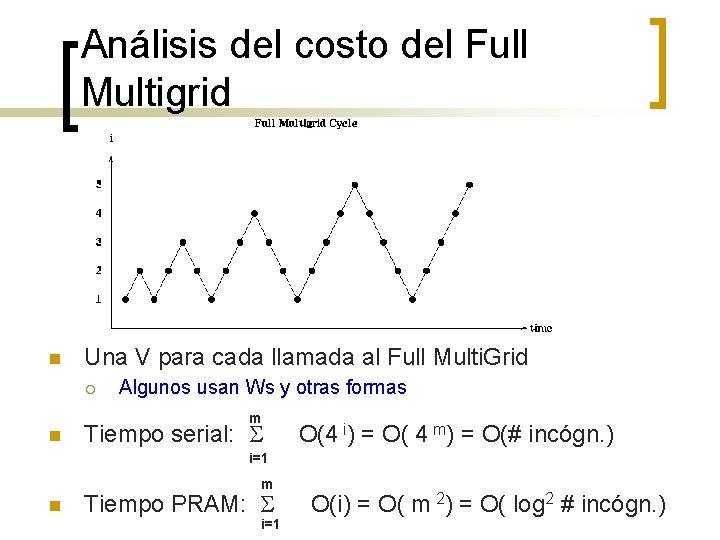
Full Multigrid (FMG) n Intuición: ¡ ¡ ¡ Mejorar la solución haciendo varios ciclos V Evitar los costosos ciclos en grilla fina (alta frecuencia) El por qué funciona es para otro curso Function FMG (b(m), x(m)) … retorna un x(m) mejorado dado un “initial guess” computa la solución exacta x(1) del P(1) for i=2 to m x(i) = MGV ( b(i), In<i-1> (x(i-1) ) ) n En otras palabras: ¡ ¡ ¡ Resolver el problema con 1 incógnita Dada la solución de un problema burdo P(i-1) , mapear los valores de la solución como el guess inicial del problema P(i) Resolver el problema más fino usando el ciclo V

Análisis del costo del Full Multigrid n Una V para cada llamada al Full Multi. Grid ¡ Algunos usan Ws y otras formas m n Tiempo serial: S O(4 i) = O( 4 m) = O(# incógn. ) i=1 m n Tiempo PRAM: S i=1 O(i) = O( m 2) = O( log 2 # incógn. )

Complejidad de resolver la Ec. Poisson n n Teorema: error después de una llamada al Full Multigrid<= c* error antes, donde c < 1/2, independentemente del # incógnitas Corolario: se puede hacer que el error se vuelva < que cualquier tolerancia fija arbitraria en n número fijo de pasos, independentemente del tamaño de la grilla fina Esta es la más importante propiedad de convergencia del Multi. Grid, que lo diferencia de otros métodos, que convergen más lento en grillas grandes (finas) Complejidad total es proporcional al costo de una llamada al FMG

El operador Solución S<i> - Detalles n n n El operador Solución, S<i>, es un Jacobi ponderado Considere este problema 1 D En el nivel i, el Jacobi puro hace: x(j) : = 1/2 (x(j-1) + x(j+1) + b(j) ) En su lugar, Jacobi ponderado hace: x(j) : = 1/3 (x(j-1) + x(j+1) + b(j) ) En 2 D, de forma similar se promedia la variable con sus vecinos.

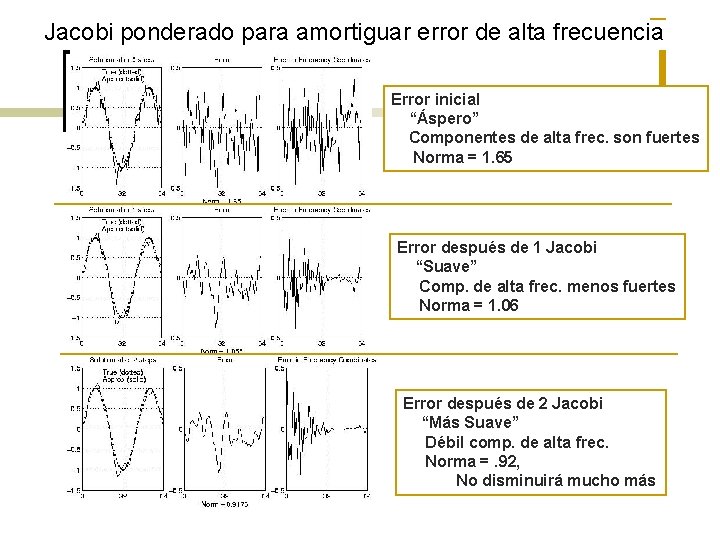
Jacobi ponderado para amortiguar error de alta frecuencia Error inicial “Áspero” Componentes de alta frec. son fuertes Norma = 1. 65 Error después de 1 Jacobi “Suave” Comp. de alta frec. menos fuertes Norma = 1. 06 Error después de 2 Jacobi “Más Suave” Débil comp. de alta frec. Norma =. 92, No disminuirá mucho más

Multigrid como algoritmo Divide y Vencerás n Cada nivel en un ciclo V reduce el error en una parte del dominio de la frecuencia

El Operador Restricción R<i> - Detalles n El operador restricción, R<i>, toma ¡ ¡ n En 1 D, se promedia los valores de los vecinos ¡ n un problema P(i) con vector del lado derecho b(i) y lo mapea en un problema más burdo P(i-1) con vector b(i-1) xburdo(i) = 1/4 * xfino(i-1) + 1/2 * xfino(i) + 1/4 * xfino(i+1) En 2 D, se promedia con los 8 vecinos (N, S, E, W, NE, NW, SE, SW)

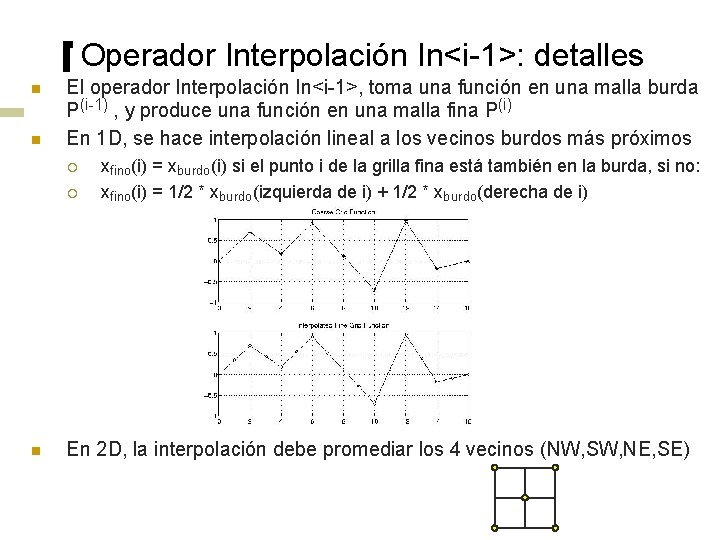
Operador Interpolación In<i-1>: detalles n n El operador Interpolación In<i-1>, toma una función en una malla burda P(i-1) , y produce una función en una malla fina P(i) En 1 D, se hace interpolación lineal a los vecinos burdos más próximos ¡ ¡ n xfino(i) = xburdo(i) si el punto i de la grilla fina está también en la burda, si no: xfino(i) = 1/2 * xburdo(izquierda de i) + 1/2 * xburdo(derecha de i) En 2 D, la interpolación debe promediar los 4 vecinos (NW, SW, NE, SE)

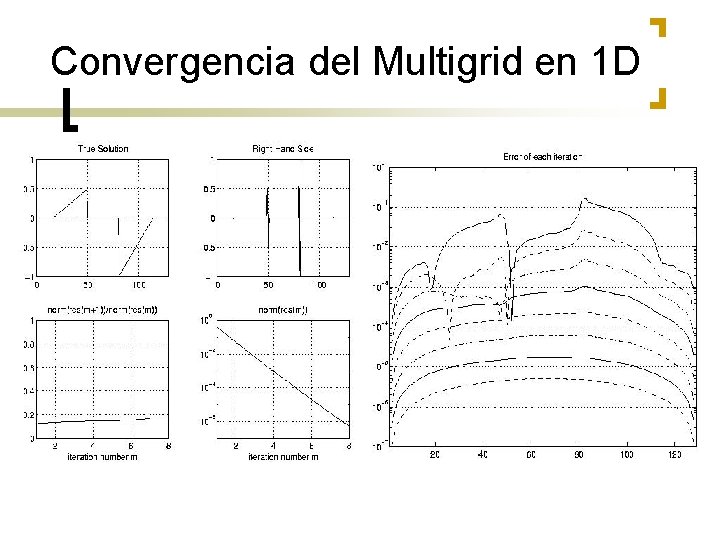
Convergencia del Multigrid en 1 D

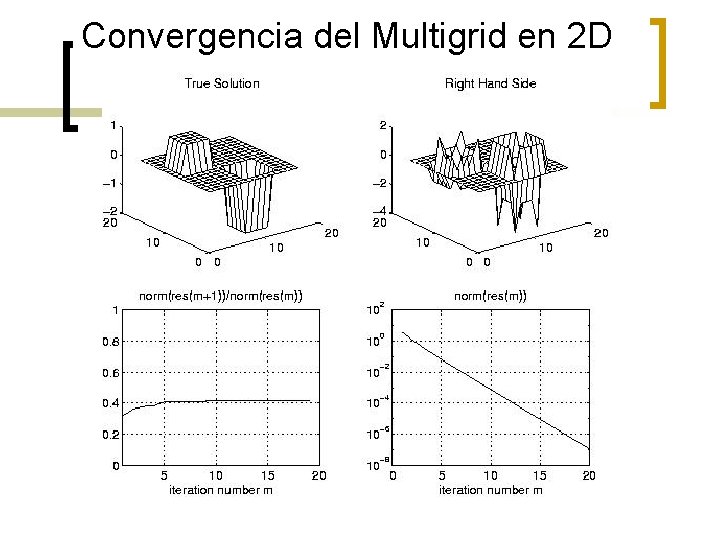
Convergencia del Multigrid en 2 D

Multigrid paralela en 2 D n n n Multigrid en 2 D necesita computar con los vecinos más próximos (hasta 8) en cada nivel de la grilla Empieza con una grilla de n=2 m+1 x 2 m+1 (aquí m=5) Se usa una malla de procesadores de s x s (aquí s=4)

Modelo de performance del Multigrid 2 D paralelo (ciclo V) n n Asumir grilla de 2 m+1 x 2 m+1 puntos, n= 2 m-1, N=n 2 Asumir p = 4 k procesadores, en una malla de 2 k x 2 k ¡ n Considerar que el Ciclo V empieza en el nivel m ¡ ¡ n Procesadores comienzan con una sub grilla de 2 m-k x 2 m-k variables En los niveles del m al k del ciclo V, cada procesador trabaja. En los noveles k-1 al 1, algunos procesadores están ociosos, por que una malla de 2 k-1 x 2 k-1 variables (o menos) no puede ocupar cada procesador Costo de un nivel en el ciclo V ¡ If nivel j >= k, then costo = O(4 j-k ) + O( 1 ) a + O( 2 j-k) b ¡ If nivel j < k, then costo = O(1) + O(1) a + O(1) b n …. Flops, proporcional al número de puntos/procesador …. Envía un número constante de mensajes a los procs. vecinos …. Número de words (doubles o floats) enviados …. Flops, proporcional al número de puntos/procesador …. Envía un número constante de mensajes a los procs. vecinos. … Número de words enviados Sume para todos los niveles 1, 2, … y todos los ciclos V en FMG!!!

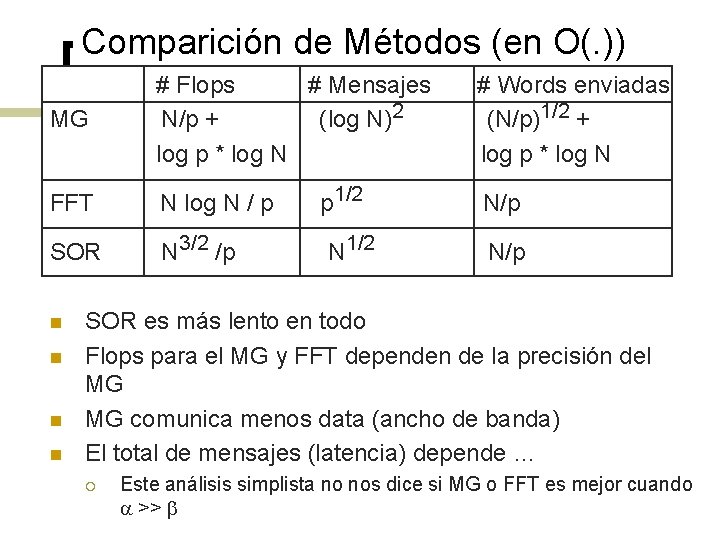
Comparición de Métodos (en O(. )) MG # Flops # Mensajes N/p + (log N)2 log p * log N FFT N log N / p SOR N 3/2 /p n n p 1/2 N 1/2 # Words enviadas (N/p)1/2 + log p * log N N/p SOR es más lento en todo Flops para el MG y FFT dependen de la precisión del MG MG comunica menos data (ancho de banda) El total de mensajes (latencia) depende … ¡ Este análisis simplista no nos dice si MG o FFT es mejor cuando a >> b

Consideraciones prácticas n n En la práctica, no tenemos que iterar hasta P(1) En programa secuencial, las grillas más burdas son rápidas, pero en un prog. paralelo no. ¡ ¡ ¡ n Considere 1000 puntos por procesador En 2 D, las vars. a comunicar es 4 xsqrt(1000) ~= 128, o 13% En 3 D, sería 1000 -83 ~= 500, o 50% Ver Tuminaro y Womble, SIAM J. Sci. Comp. , v 14, n 5, 1993 para el análisis de MG en n. CUBE 2 de 1024 procs. ¡ En grilla 64 x 64 vars. , solo 4 por procesador n ¡ En grilla 1024 x 1024 n n ¡ eficiencia de 1 ciclo V fue 0. 02, y en FMG 0. 008 eficiencias fueron 0. 7 (MG ciclo V) y 0. 42 (FMG) Aunque su eficiencia paralela es peor, FMG es 2. 6 veces más rápido que sólo los ciclos V n. CUBE tenía comunicación rápida, procesadores lentos

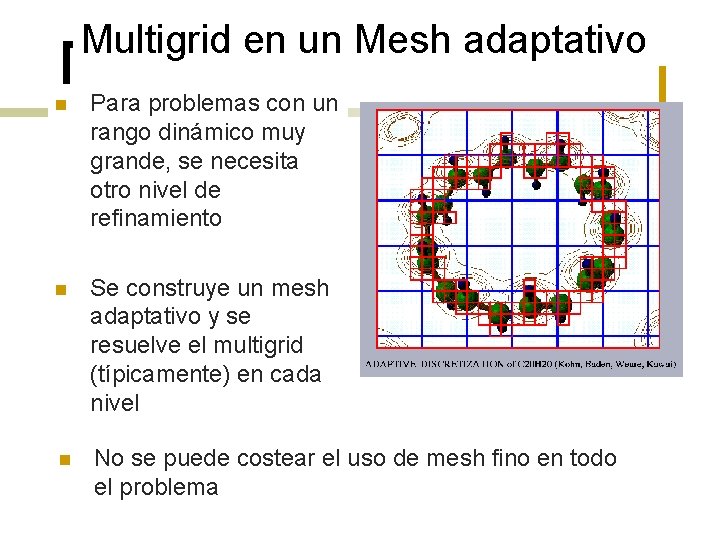
Multigrid en un Mesh adaptativo n Para problemas con un rango dinámico muy grande, se necesita otro nivel de refinamiento n Se construye un mesh adaptativo y se resuelve el multigrid (típicamente) en cada nivel n No se puede costear el uso de mesh fino en todo el problema

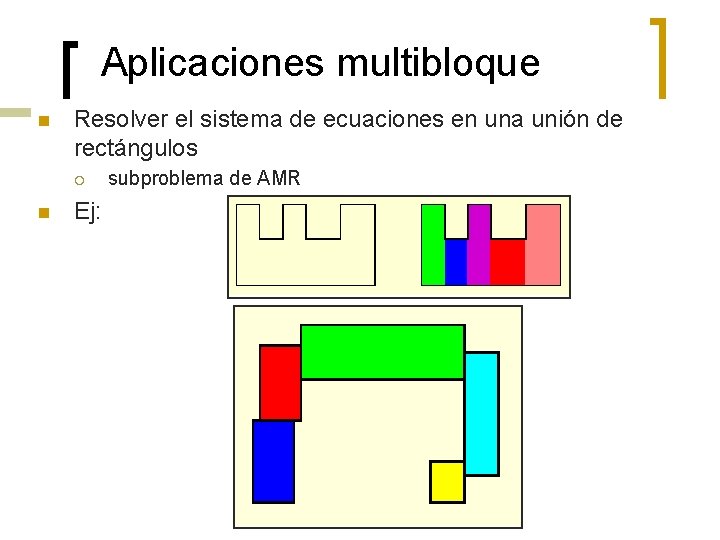
Aplicaciones multibloque n Resolver el sistema de ecuaciones en una unión de rectángulos ¡ n Ej: subproblema de AMR

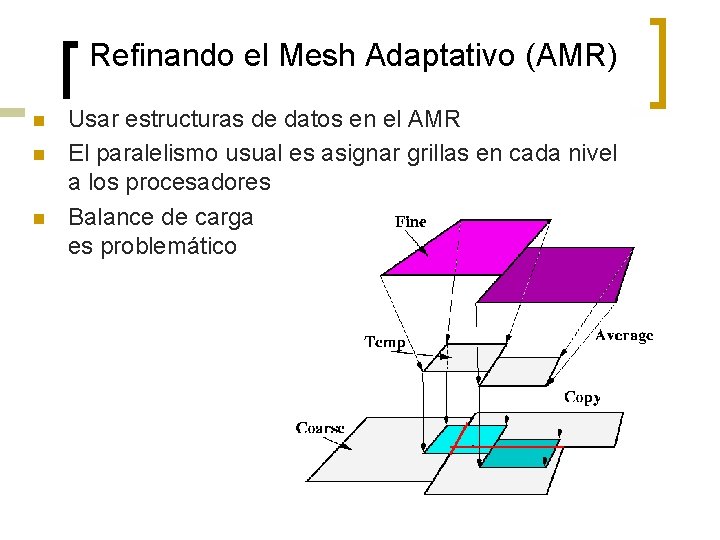
Refinando el Mesh Adaptativo (AMR) n n n Usar estructuras de datos en el AMR El paralelismo usual es asignar grillas en cada nivel a los procesadores Balance de carga es problemático

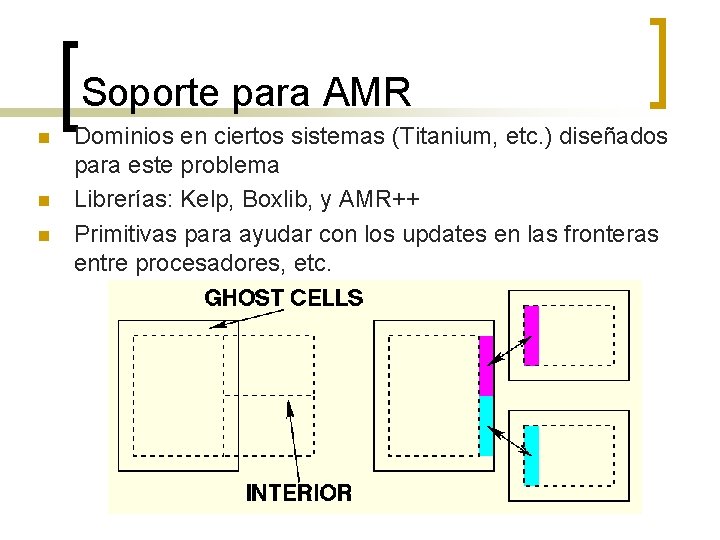
Soporte para AMR n n n Dominios en ciertos sistemas (Titanium, etc. ) diseñados para este problema Librerías: Kelp, Boxlib, y AMR++ Primitivas para ayudar con los updates en las fronteras entre procesadores, etc.

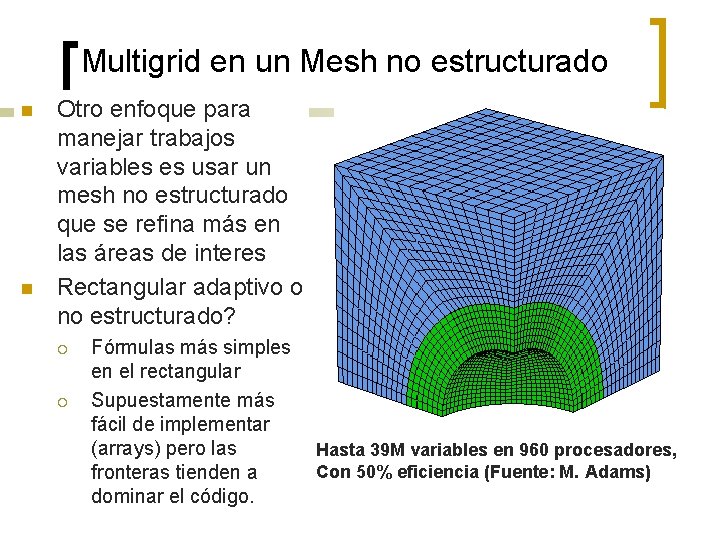
Multigrid en un Mesh no estructurado n n Otro enfoque para manejar trabajos variables es usar un mesh no estructurado que se refina más en las áreas de interes Rectangular adaptivo o no estructurado? ¡ ¡ Fórmulas más simples en el rectangular Supuestamente más fácil de implementar (arrays) pero las fronteras tienden a dominar el código. Hasta 39 M variables en 960 procesadores, Con 50% eficiencia (Fuente: M. Adams)

Multigrid en una Mesh no estructurada n n n Se necesita particionar el gráfico paralelizar Recordar: Cuál es el propósito del Multigrid? Debe poderse crear grillas burdas (problema “duro”) ¡ ¡ ¡ n Se debe redefinir R<> y In<> ¡ n Cómo convertir de grilla burda a fina y viceversa? Definir S<> ¡ n No se puede “saltearse los puntos uno si otro no” como antes Usar de nuevo “maximal independent sets” Como hacer que un grafo burdo aproxime bien al fino? ? ? Cómo se computa la matriz? (fórmulas varían) Procesar meshes burdas eficientemente ¡ ¡ Sería mejor limitarse a usar pocos procesadores en meshes burdas? Debería cambiarse el “solver” en meshes burdas?

Fuente de Mesh no estructurada (elem. finito): Vertebra Fuente: M. Adams, H. Bayraktar, T. Keaveny, P. Papadopoulos, A. Gupta

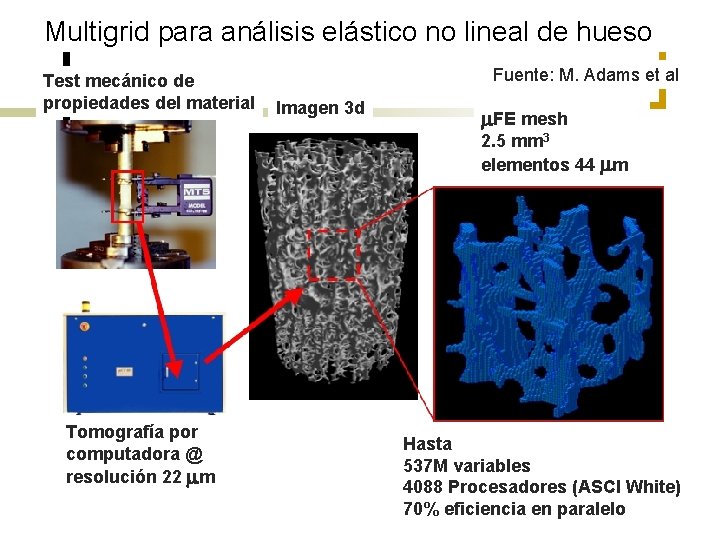
Multigrid para análisis elástico no lineal de hueso Test mecánico de propiedades del material Fuente: M. Adams et al Imagen 3 d m. FE mesh 2. 5 mm 3 elementos 44 mm Tomografía por computadora @ resolución 22 mm Hasta 537 M variables 4088 Procesadores (ASCI White) 70% eficiencia en paralelo