SISTEMA DE NUMERACIN Definicin de Numeracin v Definicin

SISTEMA DE NUMERACIÓN

Definición de Numeración v Definición de numeración: Es la parte de la aritmética que estudia la correcta formación, lectura y escritura de los números. v Cantidad: Es todo aquello susceptible de aumento o disminución. v Número: Es la idea matemática, creada por el hombre para cuantificar las cantidades. Ejemplo : 38; 892; 2013; …etc. v Numeral: Es la representación simbólica o figurativa del número. Ejemplo : 5 ; V , cinco v Cifra o dígito: Son los símbolos que por convención se usarán en la formación de numerales. Estos son: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.

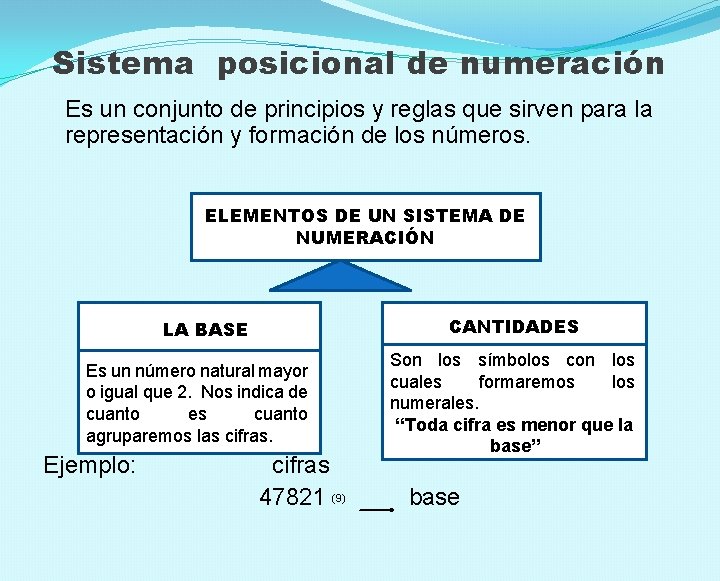
Sistema posicional de numeración Es un conjunto de principios y reglas que sirven para la representación y formación de los números. ELEMENTOS DE UN SISTEMA DE NUMERACIÓN LLA BASE CANTIDADES Es un número natural mayor o igual que 2. Nos indica de cuanto es cuanto agruparemos las cifras. Son los símbolos con los cuales formaremos los numerales. “Toda cifra es menor que la base” Ejemplo: cifras 47821 (9) base

SISTEMA DE NUMERACION DECIMAL Llamado DECÚPLO, su principio principal, es que la formación de sus unidades va de diez en diez Sus características son: � Tiene diez símbolos denominados cifras, que son : 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. � Con estas diez cifras se pueden formar todos los valores posibles mediante combinaciones entre ellos. � El mínimo valor que puede tomar un número es cero (cifra no significativa) y el máximo valor es 9 (una unidad menos que la base diez) Orden de una cifra: Se llama orden a la posición que ocupa cada cifra dentro de un número, estas órdenes se considera de derecha a izquierda. Ejemplo: 1 2 3 4 1 er orden o unidades 2 do orden o decenas 3 er orden o centenas 4 to orden o unidades de millar

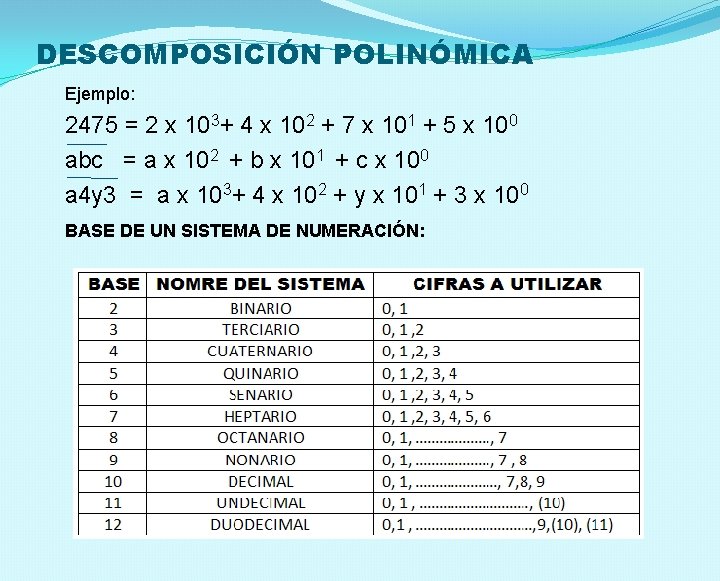
DESCOMPOSICIÓN POLINÓMICA Ejemplo: 2475 = 2 x 103+ 4 x 102 + 7 x 101 + 5 x 100 abc = a x 102 + b x 101 + c x 100 a 4 y 3 = a x 103+ 4 x 102 + y x 101 + 3 x 100 BASE DE UN SISTEMA DE NUMERACIÓN:

REPRESENTACIÓN LITERAL DE NUMERALES v Toda expresión entre paréntesis nos indicará una cifra. v Las letras diferentes no necesariamente representan valores diferentes, excepto que se indique deben ser valores diferentes. v La primera cifra de una numeral debe ser diferente de cero. Ejemplos: ab numeral de dos cifras de base 10 ( 10; 11; ………………. . 99) abc (7) numeral de tres cifras de base 7 ( 100 (7); 101(7) ; ……………. . 666(7) ) (ab) (a+2) (b+3) (8) es un numeral de tres cifras de base 8. NUMERAL CAPICUA: Es aquel número que visto y ledo de derecha a izquierda y viceversa nos presenta el mismo numeral. Ejemplo: De 2 cifras : aa ; 22 De 3 cifras: aba ; 121; 313 De 4 cifras: abba; 1221; 4444 (7 De 5 cifras: abcba; 35753(9) ;

CONVERSIÓN DE UNA BASE A OTRA Se presenta tres casos: i. Cuando se pasa de cualquier base (n) a base 10 ii. Cuando se pada de 10 a cualquier base(n) iii. Cuando se pasa de una base cualquiera (n) a otra base (m) 1 er Caso: de Base (n) a Base 10: Se aplica la descomposición polinómica del número y efectuar las operaciones indicadas, o también aplicar el Método de Ruffini. Ejemplo: Convertir 2514 (8) a base 10 Por descomposición polinómica 2514 (8) = 2 x 83 + 5 x 82 + 1 x 8 + 4 = 2 x 512 + 5 x 64 + 1 x 8 + 4 = 1024 + 320 + 8 + 4 = 1356 Por Método de Ruffini : Esquema : 2 5 1 4 Base 8 2 16 168 21 169 1352 1356 2514 (8) = 1356

2 do Caso: de base 10 a base “n” Proceso: S i: c 3 < b N = c 3 r 3 r 2 r 1 ( b) Para obtener el resultado colocamos las cifras según el orden; siendo del último cociente al primer residuo.

3 er Caso: de Base “n” a Base “m” ( n y m 10 ) Se utiliza en este caso los dos métodos vistos anteriormente, es decir: 1. Llevamos el número de sistema diferente de 10 a base 10, por descomposición polinómica y/o método de Ruffini. 2. Luego llevamos el número hallado en el sistema decimal a la base que nos piden por divisiones sucesivas. Ejemplo: Convertir 251(7) a base cuaternario Paso 1: 251 (7) a base decimal 251 (7) = 2 x 72 + 5 x 7 + 1 = 134 Paso 2: 134 al sistema cuaternario ( base 4) 134 4 2 33 4 1 8 4 0 2 251 (7) = 2012 (4)