Sistem Persamaan Linear Persamaan Linear Definsi Garis lurus

























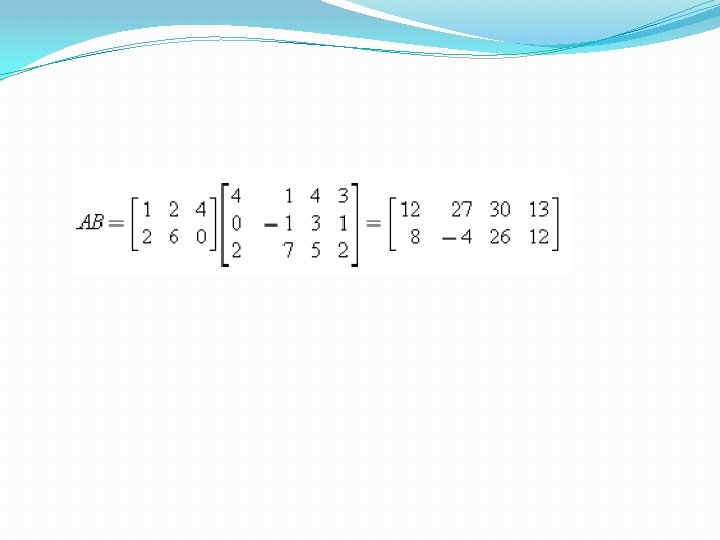
















- Slides: 43

Sistem Persamaan Linear

Persamaan Linear Definsi: �Garis lurus di bidang xy (dimensi 2) dapat dinyatakan dalam persamaan: �Jika di dimensi n (n variabel)

�Contoh persamaan linear: � 3 x=6 (titik di garis x) � 2 x+3 y=5 (garis dibidang xy) � 4 x+5 y+6 z=9 (bidang di ruang xyz)

�Contoh soal: �Temukan solusi dari persamaan linnear berikut: 1. 2 x+3 y = 6 2. 3 x+2 y+4 z=12

Sistem Persamaan Linear Definisi �Himpunan persamaan-persamaan linear dalam n variabel yang memiliki solusi berikut: 1. Tepat 1 solusi 2. Banyak solusi 3. Tidak ada solusi

�Sistem persamaan linear dengan m persamaan dan n variabel dapat dinyatakan dalam bentuk:

�Matriks Augmented

�Contoh:

Operasi Baris Elementer �Operasi Baris Elementer pada matriks augmented : 1. Mengalikan baris dengan bilangan tak nol 2. Menukar Baris 3. Menjumlahkan suatu baris dengan k kali baris lain

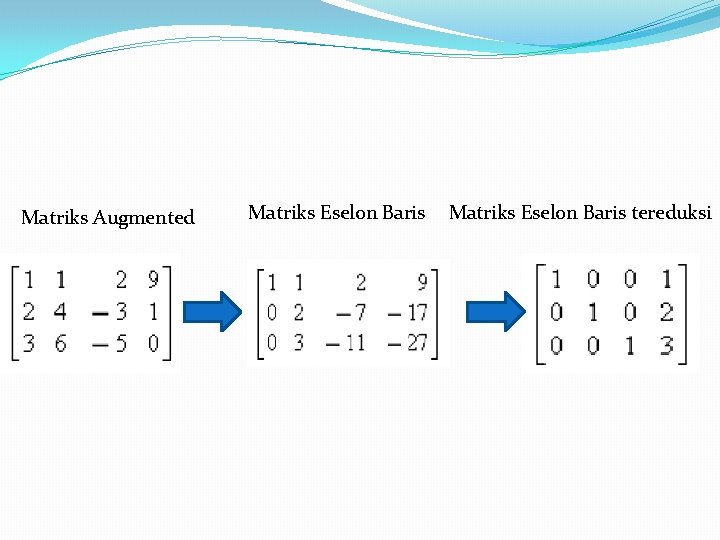
Eliminasi Gauss �Metode sistematis untuk menyelesaikan SPL �Mengubah matriks augmented menjadi matriks eselon baris

Eliminasi Gauss Jordan �Metode sistematis untuk menyelesaikan SPL �Mengubah matriks augmented menjadi matriks eselon baris tereduksi

Aturan Baris Eselon Tereduksi �Baris nol : Baris yang seluruh angka nya 0 �Baris tak nol : Baris yang mempunyai minimal 1 angka tak nol �Matriks Eselon Baris: 1. Jika baris pertama adalah baris tak nol maka angka pertama di baris tersebut harus angka 1 ( satu utama). 2. Jika suatu baris adalah baris nol maka dikelompokkan di dasar matriks 3. Jika 2 baris tak nol berurutan maka satu utama pada baris yang lebih bawah harus terletak dikanan satu utama pada baris yang diatasnya. 4. Angka-angka pada matriks selain satu utama adalah 0 ( Baris eselon tereduksi).

Matriks Augmented Matriks Eselon Baris tereduksi



�Sistem persamaan linear disebut homogen jika semua konstanta bernilai 0.

Matriks dan operasi matriks �Definisi: �Sekumpulan angka 2 yang disusun dalam bentuk baris dan kolom �Anggota 2 nya disebut entri

�Matriks bujur Sangkar : Matriks yang mempunyai diagonal utama �Matriks diagonal : Matriks bujur sangkar yang entri selain diagonal utama bernilai 0 �Matriks identitas : Matriks diagonal yang entrinya bernilai 1

�Matriks segitiga atas: Matriks bujur sangkar yang entri dibawah diagonal utama bernilai 0 �Matriks segitiga bawah: Matriks bujur sangkar yang entri dibawah diagonal utama bernilai 0

�Perkalian Skalar

�Perkalian Matriks �Definisi: Jika terdapat matriks A berukuran mxn dan B berukuran nxr maka AB berukuran mxr. �Contoh:


�Matriks Partisi

�Contoh

Perkalian matrik sebagai kombinasi linear

�Contoh
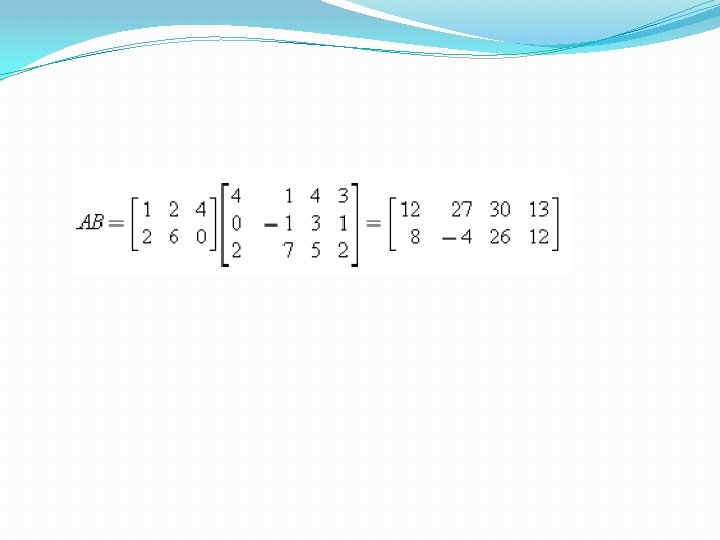

�Matriks Transpose

�Trace Matriks

�Matriks Invers

�Sifat-Sifat Matriks Invers

�Matriks Polinomial

�Matriks Elementer �Matriks nxn disebut matriks elementer jika matriks tersebut diperoleh dari matriks identitas dengan menggunakan sekali operasi baris elementer

�Operasi Baris dengan perkalian matriks �Jika matriks elementer E adalah hasil operasi baris Im dan A adalah matriks berukuran mxn maka EA adalah matriks yang sama dengan matriks hasil operasi baris elementer dari A.

�Contoh

�Setiap matriks elementer adalah matriks invertible dan inversnya merupakan matriks elementer.

�Jika A adalah matriks nxn. Pernyataan berikut eqivalen: 1. A matriks invertible 2. Ax=0 hanya punya solusi trivial 3. Bentuk eselon baris tereduksi dari A adalah I 4. A dapat dinyatakan sebagai perkalian matriks elementer.

�Contoh

�Contoh


�Jika A adalah matriks invertible maka spl Ax=b mempunyai tepat 1 solusi


�Menentukan ke konsistenan spl