SISTEM PERSAMAAN LINEAR Metode GaussJordan Bentuk Metode Gauss

SISTEM PERSAMAAN LINEAR • Metode Gauss-Jordan

Bentuk Metode Gauss • Pada metode ini yang perlu dilakukan adalah melakukan operasi pada koefisien yang ada dalam persamaan, dan hasil akhirnya adalah sistem persamaan ekivalen yang selanjutnya dapat dengan mudah diselesaikan dengan metode substitusi

Algoritma dasar metode Gauss • Secara umum sistem persamaan linear: 1. Ubahlah sistem persamaan tersebut menjadi matrik augment (berukuran n x (n+1) )

Algoritma dasar metode Gauss

Algoritma dasar metode Gauss 3. Lakukan proses triangularisasi, sehingga menjadi bentuk:

Algoritma dasar metode Gauss 4. Langkah terakhir : Lakukan proses substitusi mundur untuk memperoleh nilai x 1, x 2, x 3, …. . , xn

Penyelesaian dengan Eliminasi Gauss • Selesaikan persamaan berikut x + 2 y + z = 3 (1) 3 x - y – 3 z = -1 (2) 2 x + 3 y + z = 4 (3)

Penyelesaian dengan Eliminasi Gauss • Selesaikan persamaan berikut x + 2 y + z = 3 (1) 3 x - y – 3 z = -1 (2) 2 x + 3 y + z = 4 (3) • Penyelesaian dimulai dengan menuliskan bentuk augmented matriknya

Penyelesaian dengan Eliminasi Gauss • Kita sebut baris pertama sebagai baris poros/pivot dan entri 1 (yg dilingkari) sebagai poros/pivot • Langkah 1. – baris pertama digunakan untuk mengeliminasi elemen di kolom pertama dari baris kedua dan ketiga – baris pertama dikalikan 3 untuk mengeliminasi baris kedua – baris pertama dikalikan 2 untuk mengeliminasi baris kedua

Penyelesaian dengan Eliminasi Gauss • Langkah 2 – baris kedua digunakan untuk mengeliminasi elemen di kolom kedua dari baris ketiga – baris kedua dikalikan 1/7 untuk mengeliminasi baris

Penyelesaian dengan Eliminasi Gauss • Langkah 3: Gunakan substitusi untuk mendapatkan penyelesaian Ø Ø Baris ketiga -1/7 z = -4/7 z = 4 Baris kedua -7 y – 6 z = -10 y = -2 Baris pertama x + 2 y + z = 3 x = 3 Diperoleh x=3; y=-2; z=4

Kasus 1 • Selesaikan persamaan berikut x + 2 y + z = 2 (1) 3 x + 6 y =9 (2) 2 x + 8 y + 4 z = 6 (3)

Penyelesaian Kasus 1 baris 2 – baris 1*3 baris 3 – baris 1*2 hasil eliminasi kolom pertama baris ke-2&3 dilanjutkan dengan eliminasi kolom kedua baris ke-3 (tentukan poros/pivot) baris poros/pivot baris ke-2 poros/pivot 0 berdasarkan algoritma Gauss, poros/pivot nol(0), maka lakukan pertukaran baris dengan baris bawahnya

Penyelesaian Kasus 1 Lakukan substitusi: -3 z = 3 z = -1 4 y + 2 z = 2 4 y+ 2(-1) = 2 y = 1 1 x + 2 y + z = 2 x + 2(1) + (-1) = 2 x = 1

Kasus 2 • Masalah lain muncul bila elemen poros/pivot sangat kecil atau mendekati nol dibandingkan dengan elemen lainnya yang menyebabkan error pembulatan muncul • Contoh: Selesaikan sistem persamaan berikut dengan metode eliminasi Gauss 0, 0003 x + 1. 566 y = 1. 569 0, 3454 x – 2, 436 y = 1, 018 (dengan 4 AS, solusi sejatinya x = 10, 00 dan y = 1, 00)

Penyelesaian Kasus 2 baris 2 – baris 1*(0, 3454/0, 0003) subtitusi: -1804 y = -1805 y = 1, 001 (mendekati solusi sejati) 0, 0003 x + 1, 566 y = 1, 569 0, 0003 x + 1, 566(1, 001) = 1, 569 x = 3, 333 (jauh dari solusi sejati)

Penyelesaian Kasus 2 Karena elemen baris 1 kolom 1 sebagai poros/pivot nilainya mendekati 0(nol) lakukan pertukaran baris 1 dengan baris berikutnya baris 2 – baris 1*(0, 0003/0, 3454) subtitusi: 1568 y = 1568 y = 1, 000 (mendekati solusi sejati) 0, 3454 x – 2, 436 y = 1, 018 0, 0003 x – 2, 436(1, 000) = 1, 018 x = 10, 02 (lebih baik dari solusi sebelumnya)

Kemungkinan Solusi Sistem Persamaan Linier • Solusi unik/tunggal • Solusi banyak/tak berhingga • Tidak ada solusi
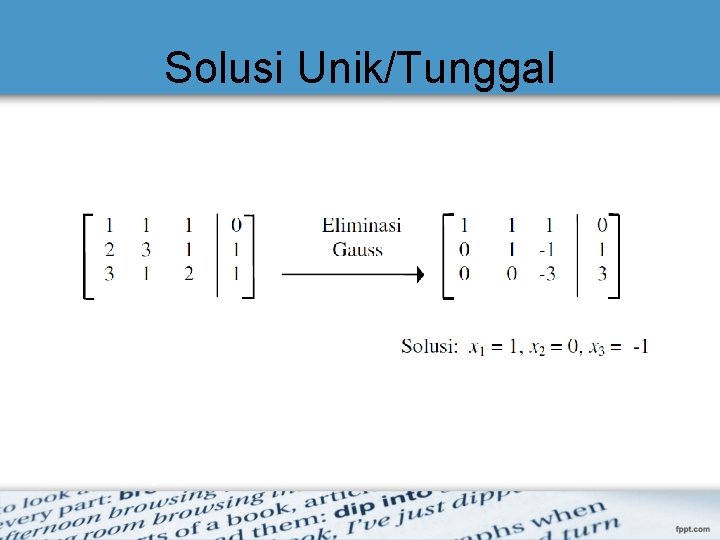
Solusi Unik/Tunggal

Solusi Banyak/Tak Berhingga • Persamaan x + 2 y + z = 1 2 x - y + z = 2 4 x + 3 y + 3 z = 4 3 x + y + 2 z = 3 diperoleh y = -1/5 z x = 1 -2 y-z 1 - 3/5 z Terlihat bahwa himpunan penyelesaian adalah semua tripel berturut bentuk (1 -3/5α, -1/5α, α) dimana α adalah bilangan real Sistem ini memiliki tak hingga banyaknya penyelesaian karena x dan y dinyatakan oleh peubah bebas z
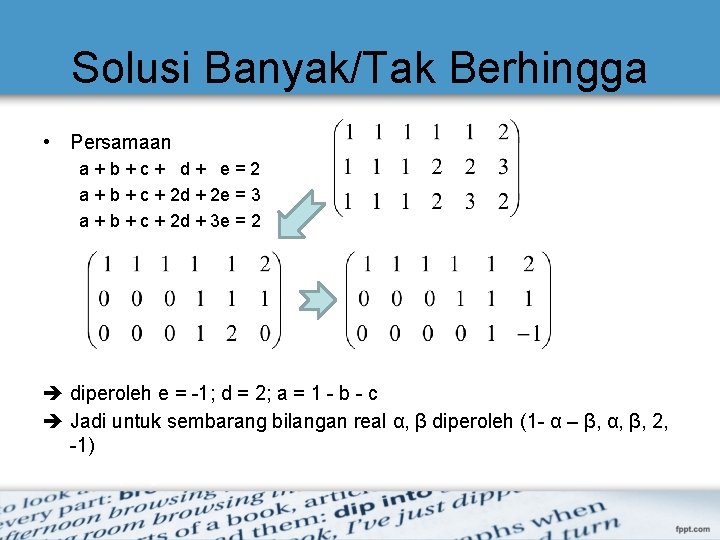
Solusi Banyak/Tak Berhingga • Persamaan a+b+c+ d+ e=2 a + b + c + 2 d + 2 e = 3 a + b + c + 2 d + 3 e = 2 diperoleh e = -1; d = 2; a = 1 - b - c Jadi untuk sembarang bilangan real α, β diperoleh (1 - α – β, α, β, 2, -1)

Tidak Ada Solusi • Persaman yang bersesuaian dengan baris ke-3 0 x + 0 y + 0 z = 1 tidak ada nilai x, y dan z yang memenuhi

Metode Gauss-Jordan • Penambahan Matrik sebelah kiri diubah menjadi matrik diagonal • Penyelesaian dari persamaan linier simultan diatas adalah nilai b 1, b 2, b 3, …, bn dan atau a 1 = b 1, a 2 = b 2, a 3 = b 3, …. , an = bn

Contoh Eliminasi Gauss-Jordan x + y + 2 z = 9 1 1 2 9 2 x + 4 y – 3 z = 1 2 4 -3 1 3 x + 6 y – 5 z = 0 3 6 -5 0

Penyelesaian dari soal contoh 1. Lakukan Eliminasi Gauss 2. mengusahakan bentuk 1 0 0 ? 0 1 0 ? 0 0 1 ?

Penyelesaian dari soal contoh 1. Lakukan Eliminasi Gauss 2. mengusahakan bentuk 1 0 0 ? 0 1 0 ? 0 0 1 ?
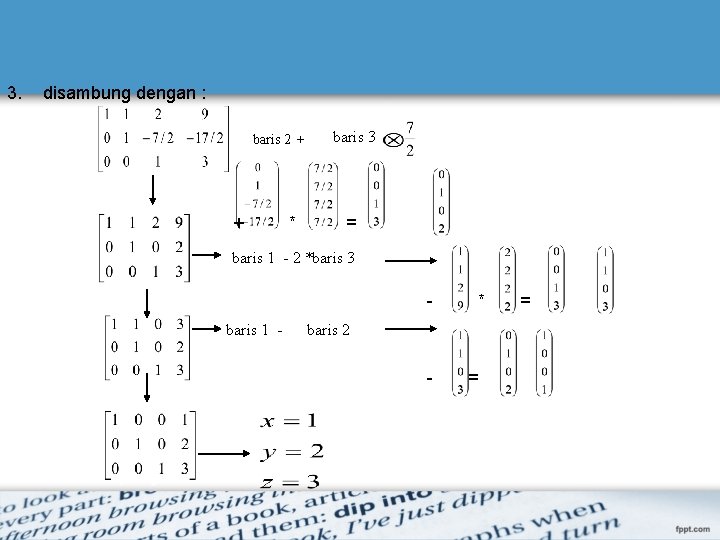
3. disambung dengan : baris 2 + + * baris 3 = baris 1 - 2 *baris 3 baris 1 - * baris 2 - = =
- Slides: 27