Sistem Persamaan Linear Dua Variabel SPLDV Sistem persamaan

Sistem Persamaan Linear Dua Variabel ( SPLDV ) Sistem persamaan linear dua variabel adlh sistem persamaan yg mengandung dua variabel yg tdk diketahui. Bentuk Umumnya : ax + by = c … persamaan (1) px + qy = r … persamaan (2) Dg a, b, c, p, q & r ϵ R a, p = koefisien dari x b, q = koefisien dari y Ada 4 metode penyelesaian SPLDV tsb, yaitu : 1) Metode Eliminasi 2) Metode Substitusi 3) Metode Campuran 4) Metode Determinan

1. Metode Eliminasi Metode ini digunakan dg cara mengeliminasi (menghilangkan) salah satu variabelnya, shg diperoleh sebuah persamaan dg satu variabel. Contoh : Tentukan Himpunan Penyelesaian (HP) dari persamaan linear berikut dg metode eliminasi ! 2 x + 3 y = 1 … pers. (1) 3 x + y = 5 … pers. (2) Jawab : Mengeliminasi x 2 x + 3 y = 1 x 3 6 x + 9 y = 3 3 x + y = 5 x 2 6 x + 2 y = 10 – 7 y = - 7 y = -1

Mengeliminasi y 2 x + 3 y = 1 x 1 3 x + y = 5 x 3 2 x + 3 y = 1 9 x + 3 y = 15 – - 7 x = - 14 x=2 Jd, HP = { 2, -1 } Catatan : “ Jika kita mengeliminasi (menghilangkan) variabel x maka yg akan kita dapatkan nantinya adlh nilai dari variabel y dan sebaliknya, jika kita mengeliminasi variabel y maka yg akan kita dapatkan nantinya adlh nilai dari variabel x “

Tentukan HP dari SPL berikut ini dg menggunakan metode eliminasi ! 1) 2 x – y = 2 3 x – 2 y = 1 Jawab 2) 3 x + 5 y = 4 3 x – y = 10 Jawab 3) 5 x + y = 5 17 x + y = - 5 Jawab 4) 2 p – 3 q = 4 7 p + 2 q = 39 Jawab Ke slide Metode Substitusi

Jawab 1) * Mengeliminasi variabel y 2 x – y = 2 x 2 4 x – 2 y = 4 3 x – 2 y = 1 x 1 3 x – 2 y = 1 x=3 * Mengeliminasi variabel x 2 x – y = 2 x 3 3 x – 2 y = 1 x 2 6 x – 3 y = 6 6 x – 4 y = 2 y=4 Jd, HP = { 3, 4} Kembali ke slide soal

Jawab 2) * Mengeliminasi variabel x 3 x + 5 y = 4 3 x – y = 10 6 y = - 6 y=-1 * Mengeliminasi variabel y 3 x + 5 y = 4 x 1 3 x – y = 10 x 5 3 x + 5 y = 4 15 x – 5 y = 50 + 18 x = 54 x=3 Jd, HP = { 3, - 1} Kembali ke slide soal

Jawab 3) * Mengeliminasi variabel y 5 x + y = 5 17 x + y = - 5 - 12 x = 10 * Mengeliminasi variabel x 5 x + y = 5 x 17 17 x + y = - 5 x 5 85 x + 17 y = 85 85 x + 5 y = - 25 12 y = 110 Kembali ke slide soal

Jawab 4) * Mengeliminasi variabel p 2 p – 3 q = 4 x 7 14 p – 21 q = 28 7 p + 2 q = 39 x 2 14 p + 4 q = 78 - 25 q = - 50 * Mengeliminasi variabel q 2 p – 3 q = 4 x 2 7 p + 2 q = 39 x - 3 4 p – 6 q = 8 - 21 p - 6 q = - 117 25 p = 125 Jd, HP = { 5, 2} Kembali ke slide soal

2. Metode Substitusi Pada metode ini, salah satu variabel dari salah satu persamaan disubstitusikan shg diperoleh sebuah persamaan dg satu variabel saja Contoh : a) Tentukan HP dari persamaan linear berikut dg metode substitusi ! 3 x + 4 y = 11 … pers. (1) x + 7 y = 15 … pers. (2) Jawab : Dari pers. (2) didapat : x = 15 – 7 y … pers. (3) Kmd substitusikan pers. (3) ke pers. (1) : 3 x + 4 y = 11 Harga y = 2 kmd

b) Tentukan HP dari persamaan linear berikut dg metode substitusi ! 2 x + 3 y = 1 … pers. (1) 3 x + y = 5 … pers. (2) Jawab : Dari pers. (2) didapat : y = 5 – 3 x … pers. (3). Kmd substitusikan pers. (3) ke pers. (1) : Harga x = 2 kmd disubstitusikan ke pers. (3) : 2 x + 3 y = 1 2 x + 3(5 – 3 x) = 1 2 x + 15 – 9 x = 1 2 x – 9 x = 1 – 15 - 7 x = - 14 x=2 y = 5 – 3 x y = 5 – 3(2) y=5– 6 y=-1 Jd, HP = { 2, - 1}

Tentukan HP dari SPL berikut ini dg menggunakan metode substitusi ! 1) 2) 3) 4) 2 x – y = 2 3 x – 2 y = 1 Jawab 3 x + 5 y = 4 3 x – y = 10 Jawab 5 x + y = 5 17 x + y = - 5 Jawab 2 p – 3 q = 4 7 p + 2 q = 39 Jawab

Jawab 1) 2 x – y = 2 … pers. (1) 3 x – 2 y = 1 … pers. (2) Dari pers. (1) didapat : Harga x - y = 2 – 2 x ⇔ y ke pers. (1) : = - 2 + 2 x … pers. (3) Kmd substitusikan pers. (3) ke pers. (2) : ⇔ 3 x – 2 y = 1 ⇔ 3 x – 2(-2 + 2 x) = 1 ⇔ 3 x + 4 – 4 x = 1 ⇔ 3 x – 4 x = 1 – 4 ⇔-x=-3 ⇔x=3 = 3 kmd disubstitusikan 2 x – y = 2 ⇔ 2(3) – y = 2 ⇔ 6–y=2 ⇔-y=2– 6 ⇔-y=-4 ⇔y=4 Jd, HP = { 3, 4}

Jawab 2) 3 x + 5 y = 4 … pers. (1) 3 x – y = 10 … pers. (2) Dari pers. (2) didapat : - y = 10 – 3 x ⇔ y Harga x = 3 kmd disubstitusikan = - 10 + 3 x … pers. (3) ke pers. (2) : Kmd substitusikan pers. (3) ke pers. (1) : 3 x – y = 10 ⇔ 3 x + 5 y = 4 ⇔ 3(3) – y = 10 ⇔ 3 x + 5(-10 + 3 x) = 4 ⇔ 9 – y = 10 ⇔ 3 x – 50 + 15 x = 4 ⇔ - y = 10 – 9 ⇔ 3 x + 15 x = 4 + 50 ⇔-y=1 ⇔ 18 x = 54 ⇔y=-1 ⇔x=3 Jd, HP = { 3, - 1 }

Jawab 3) 5 x + y = 5 … pers. (1) 17 x + y = - 5 … pers. (2) Dari pers. (1) didapat : Harga y = 5 – 5 x … pers. (3) kmd disubstitusikan ke pers. (1) : Kmd substitusikan pers. (3) ke pers. (2) : 5 x + y = 5 17 x + y = - 5 ⇔ 17 x + 5 – 5 x = - 5 ⇔ 17 x – 5 x = - 5 – 5 ⇔ 12 x = - 10 (x 6) ⇔ - 25 + 6 y = 30 ⇔ 6 y = 30 + 25 ⇔ 6 y = 55

Jawab 4) 2 p – 3 q = 4 … pers. (1) 7 p + 2 q = 39 … pers. (2) Harga q = 2 kmd disubstitusikan ke pers. (1) : Dari pers. (1) didapat : 2 p – 3 q = 4 ⇔ 2 p = 4 + 3 q Kmd substitusikan pers. (3) ke pers. (2) : ⇔ 7 p + 2 q = 39 2 p – 3 q = 4 ⇔ 2 p – 3(2) = 4 ⇔ 2 p – 6 = 4 ⇔ 2 p = 4 + 6 ⇔ 2 p = 10 ⇔p=5 ( x 2) ⇔ 28 + 21 q + 4 q = 78 ⇔ 21 q + 4 q = 78 – 28 ⇔ 25 q = 50 ⇔ q = 2 Jd, HP = { 5, 2 }

3. Metode Campuran Pada metode ini, merupakan gabungan dari cara eliminasi dan substitusi. Contoh : a) Tentukan HP dari persamaan linear berikut dg metode campuran ! 3 x + 4 y = 11 … pers. (1) x + 7 y = 15 … pers. (2) Jawab : 3 x + 4 y = 11 x 1 3 x + 4 y = 11 x + 7 y = 15 x 3 3 x + 21 y = 45 - 17 y = - 34 ⇔y=2 Harga y = 2 kmd substitusikan ke pers(2) : x + 7 y = 15 ⇔ x + 7(2) = 15 ⇔ x + 14 = 15

b) Tentukan HP Dari Persamaan Linear Berikut Dg Metode Campuran ! 2 x + 3 y = 1 … pers. (1) 4 x – 3 y = 11 … pers. (2) Jawab : 2 x + 3 y = 1 4 x – 3 y = 11 + ⇔ 6 x = 12 ⇔x=2 Harga x = 2 kmd substitusikan ke pers. (1) : 2 x + 3 y = 1 ⇔ 2(2) + 3 y = 1 ⇔ 4 + 3 y = 1 ⇔ 3 y = 1 – 4 ⇔ 3 y = - 3 ⇔y=-1 Jd, HP = { 2, -1 }

Tentukan HP Dari SPL Berikut Ini dg Menggunakan Metode Campuran ! 1) 2) 5 x + y = 5 17 x + y = - 5 Jawab 2 p – 3 q = 4 7 p + 2 q = 39 Jawab

Jawab 1) 5 x + y = 5 … pers. (1) 17 x + y = - 5 … pers(2) 5 x + y = 5 17 x + y = - 5 - 12 x = 10 Harga kmd disubstitusikan ke pers(1) : 5 x + y = 5 (x 6) ⇔ - 25 + 6 y = 30 ⇔ 6 y = 30 + 25 ⇔ 6 y = 55
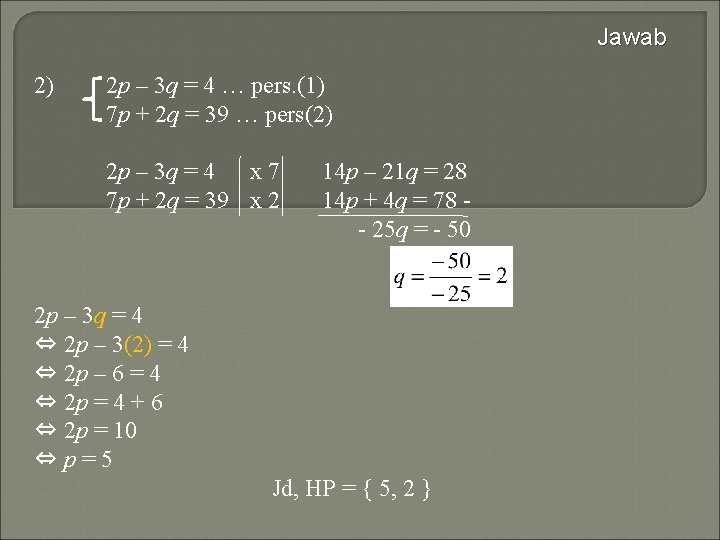
Jawab 2) 2 p – 3 q = 4 … pers. (1) 7 p + 2 q = 39 … pers(2) 2 p – 3 q = 4 x 7 7 p + 2 q = 39 x 2 14 p – 21 q = 28 14 p + 4 q = 78 - 25 q = - 50 2 p – 3 q = 4 ⇔ 2 p – 3(2) = 4 ⇔ 2 p – 6 = 4 ⇔ 2 p = 4 + 6 ⇔ 2 p = 10 ⇔p=5 Jd, HP = { 5, 2 }

4. Metode Determinan Sistem persamaan, misalkan : ax + by = c px + qy = r Menurut aturan determinan diubah mjd : Artinya dan y didefinisikan : dan utk variabel x ,

Contoh : Tentukan HP dari SPL berikut ! 4 x – 5 y = 22 7 x + 3 y = 15 Kita cari dl determinannya : Jd, HP = { 3, -2}

Tentukan HP Dari SPL Berikut Ini dg Menggunakan Metode Determinan ! 1) 2 x – y = 2 3 x – 2 y = 1 Jawab 2) 3 x + 5 y = 4 3 x – y = 10 Jawab

Jawab 1) 2 x – y = 2 3 x – 2 y = 1 Kita cari dl determinannya : Jd, HP = { 3, 4}

Jawab 2) 3 x + 5 y = 4 3 x – y = 10 Kita cari dl determinannya : Jd, HP = { 3, -1}
- Slides: 25












































