SISTEM KOORDINAT HORISONTAL 1 Sistem Koordinat Lokal 2

SISTEM KOORDINAT HORISONTAL • 1. Sistem Koordinat Lokal • 2. Sistem Koordinat Umum

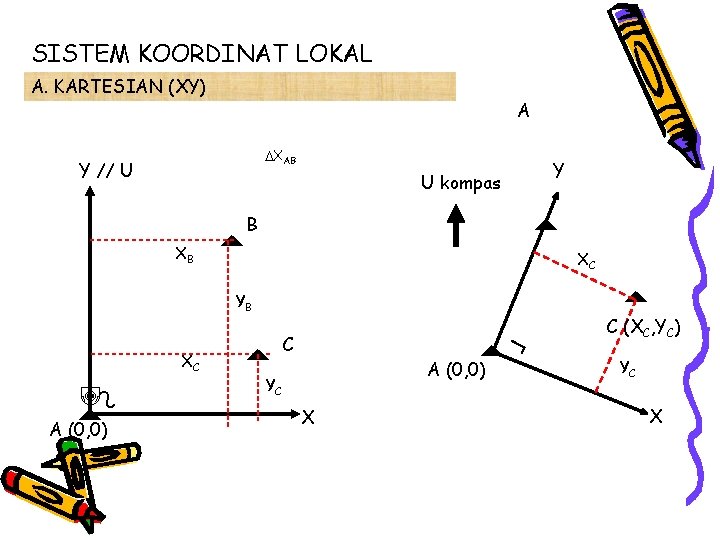
SISTEM KOORDINAT LOKAL A. KARTESIAN (XY) A XAB Y // U Y U kompas B XB XC YB XC A (0, 0) C A (0, 0) YC X C (XC, YC) YC X

METODE PENENTUAN POSISI HORISONTAL • Menentukan koordinat titik baru dari satu atau beberapa titik yg telah diketahui koordinatnya • Dikelompokkan dalam : 1. Metode penentuan titik tunggal (satu titik) 2. Metode penentuan banyak titik

Metode Penentuan Satu Titik • Metode Polar • Metode Perpotongan ke muka • Metode Perpotongan ke belakang

Metode Penentuan Banyak Titik • Metode Polygoon • Metode Triangulasi • Metode Trilaterasi

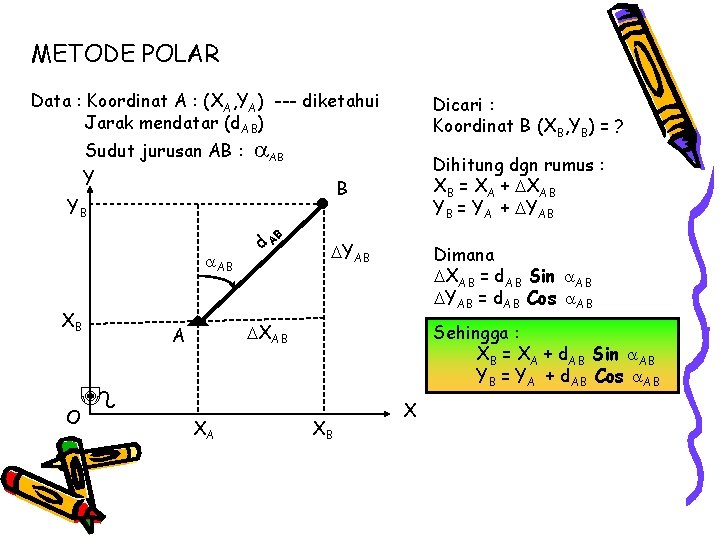
METODE POLAR Data : Koordinat A : (XA, YA) --- diketahui Jarak mendatar (d. AB) Sudut jurusan AB : Y AB YB B AB XB O A XA Dicari : Koordinat B (XB, YB) = ? d. A Dihitung dgn rumus : XB = XA + XAB YB = YA + YAB B YAB Dimana XAB = d. AB Sin AB YAB = d. AB Cos AB Sehingga : XB = XA + d. AB Sin AB YB = YA + d. AB Cos AB XAB XB X

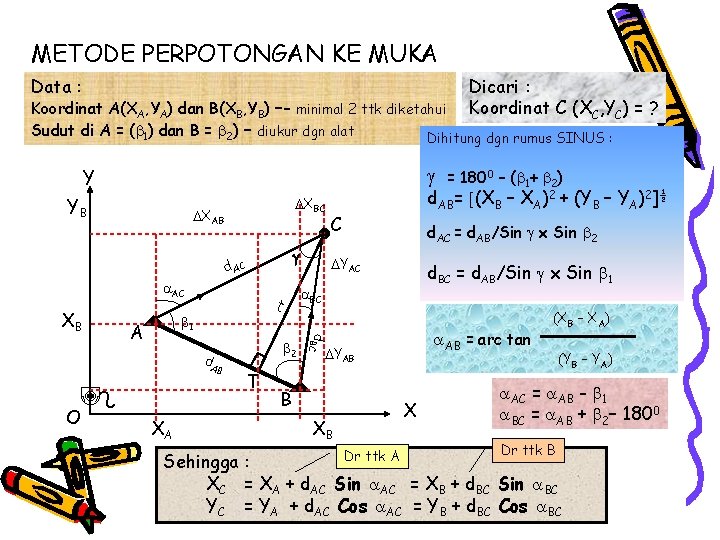
METODE PERPOTONGAN KE MUKA Data : Dicari : Koordinat C (XC, YC) = ? Koordinat A(XA, YA) dan B(XB, YB) –- minimal 2 ttk diketahui Sudut di A = ( 1) dan B = 2) – diukur dgn alat Dihitung dgn rumus SINUS : Y YB C d AC AC 1 d. A B O XA T YAC d. BC = d. AB/Sin x Sin 1 BC t A d. AC = d. AB/Sin x Sin 2 2 AB = arc tan d. BC XB d. AB= (XB – XA)2 + (YB – YA)2]½ XBC XAB = 1800 – ( 1+ 2) YAB B X XB Dr ttk A (XB – XA) (YB – YA) AC = AB - 1 BC = AB + 2– 1800 Dr ttk B Sehingga : XC = XA + d. AC Sin AC = XB + d. BC Sin BC YC = YA + d. AC Cos AC = YB + d. BC Cos BC

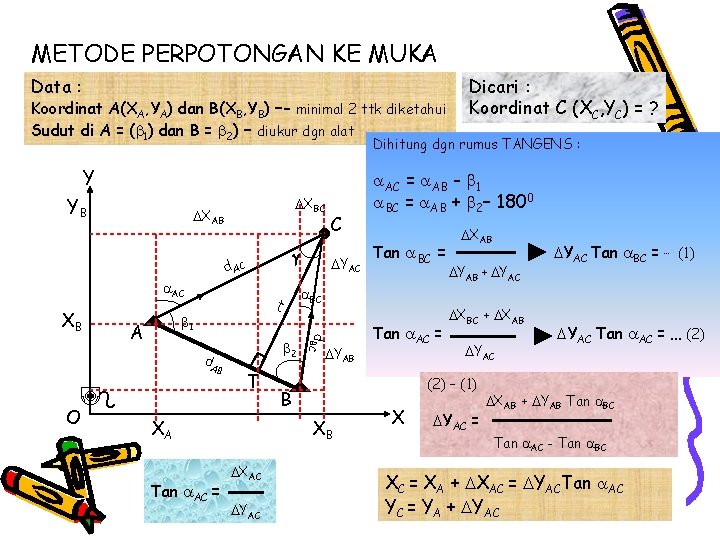
METODE PERPOTONGAN KE MUKA Data : Koordinat A(XA, YA) dan B(XB, YB) –- minimal 2 ttk diketahui Sudut di A = ( 1) dan B = 2) – diukur dgn alat Dicari : Koordinat C (XC, YC) = ? Dihitung dgn rumus TANGENS : Y YB XBC XAB C d AC AC 1 d. A B O A T XA Tan AC = 2 YAB B XB XAC YAC Tan BC = BC t d. BC XB YAC AC = AB - 1 BC = AB + 2– 1800 Tan AC = XAB YAB + YAC XBC + XAB YAC (2) – (1) X YAC = YAC Tan BC = … (1) YAC Tan AC = … (2) XAB + YAB Tan BC Tan AC - Tan BC XC = XA + XAC = YACTan AC YC = YA + YAC

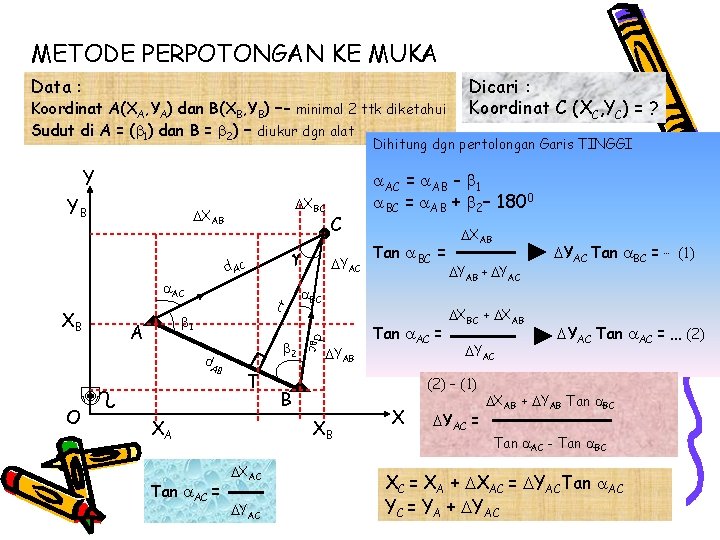
METODE PERPOTONGAN KE MUKA Data : Koordinat A(XA, YA) dan B(XB, YB) –- minimal 2 ttk diketahui Sudut di A = ( 1) dan B = 2) – diukur dgn alat Dicari : Koordinat C (XC, YC) = ? Dihitung dgn pertolongan Garis TINGGI Y YB XBC XAB C d AC AC 1 d. A B O A T XA Tan AC = 2 YAB B XB XAC YAC Tan BC = BC t d. BC XB YAC AC = AB - 1 BC = AB + 2– 1800 Tan AC = XAB YAB + YAC XBC + XAB YAC (2) – (1) X YAC = YAC Tan BC = … (1) YAC Tan AC = … (2) XAB + YAB Tan BC Tan AC - Tan BC XC = XA + XAC = YACTan AC YC = YA + YAC

1. Diket titik A(10, 10) m Sdt jur AB = 900 Jarak mendatar AB = 100 m Koordinat B (XB, YB) = ? ? 2. Diket titik A(10 N, 10 N) m Sdt jur AB = 900 Jarak mendatar AB = 100 m Koordinat B (XB, YB) = ? ?

3. Diket titik A(10, 10) m ; B(10, 70) Sdt BAC = Sdt ABC = 600 Koordinat C (XC, YC) = ? ? 4. Diket titik A(-10, -10) m ; B(-10, -70) Sdt BAC = Sdt ABC = 600 Koordinat C (XC, YC) = ? ?