SISTEM BILANGAN Pendahuluan Ada beberapa sistem bilangan yang

SISTEM BILANGAN

Pendahuluan § Ada beberapa sistem bilangan yang digunakan dalam sistem digital. Yang paling umum adalah sistem bilangan desimal, biner, oktal dan heksadesimal § Sistem bilangan desimal merupakan sistem bilangan yang paling familier dengan kita karena berbagai kemudahannya yang kita pergunakan sehari – hari.

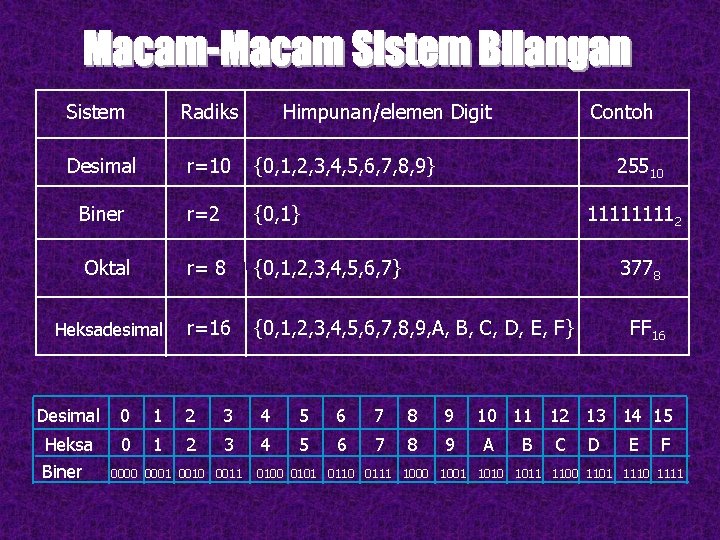
Sistem Radiks Himpunan/elemen Digit Desimal r=10 {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Biner r=2 {0, 1} Oktal r= 8 {0, 1, 2, 3, 4, 5, 6, 7} Heksadesimal r=16 {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F} 255 10 1111 2 377 8 Desimal 0 1 2 3 4 5 6 7 8 9 Heksa Biner 0 1 2 3 4 5 6 7 8 9 0000 0001 0010 0011 Contoh FF 16 10 11 12 13 14 15 A B C D E F 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

SISTEM BILANGAN § § Sistem Bilangan Desimal Sistem Bilangan Biner Sistem Bilangan Oktal Sistem Bilangan Heksadesimal

Sistem Bilangan Desimal § Basis 10 § Bilangan : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Lanjutan Sistem Bilangan Desimal. . Contoh : Angka 321 dengan dasar 10 maka : (3 * 102) + (2 * 101) + (1 * 100) = 321 Angka 4532 dengan dasar 10 maka : (4 * 103) + (5 * 102) + (3 * 101) + (2 * 100) = 4532

Konversi Radiks-r ke desimal § Rumus konversi radiks-r ke desimal: § Contoh: – 11012 = 1 23 + 1 22 + 1 20 = 8 + 4 + 1 = 1310 – 5728 = 5 82 + 7 81 + 2 80 = 320 + 56 + 16 = 39210 – 2 A 16 = 2 161 + 10 160 = 32 + 10 = 4210

Konversi Bilangan Desimal ke Biner § Konversi bilangan desimal bulat ke bilangan Biner: Gunakan pembagian dgn 2 secara suksesif sampai sisanya = 0. Sisa-sisa pembagian membentuk jawaban, yaitu sisa yang pertama akan menjadi least significant bit (LSB) dan sisa yang terakhir menjadi most significant bit (MSB).

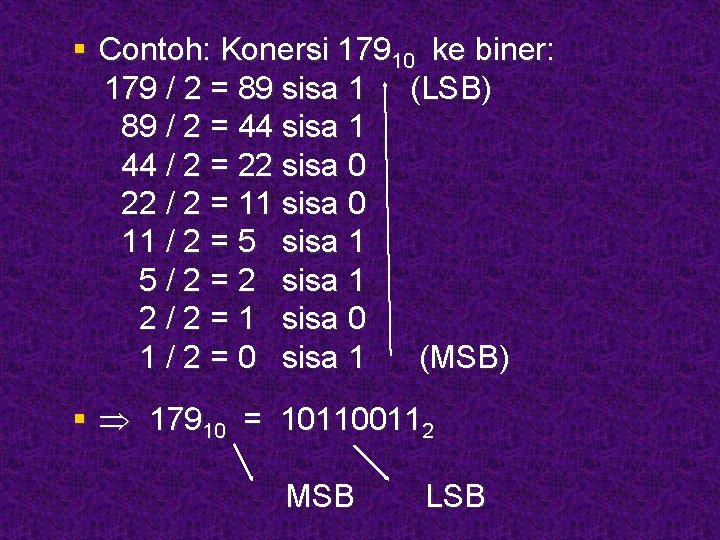
§ Contoh: Konersi 17910 ke biner: 179 / 2 = 89 sisa 1 (LSB) 89 / 2 = 44 sisa 1 44 / 2 = 22 sisa 0 22 / 2 = 11 sisa 0 11 / 2 = 5 sisa 1 5 / 2 = 2 sisa 1 2 / 2 = 1 sisa 0 1 / 2 = 0 sisa 1 (MSB) § 17910 = 101100112 MSB LSB

Konversi Bilangan Desimal ke Oktal § Konversi bilangan desimal bulat ke bilangan oktal: Gunakan pembagian dgn 8 secara suksesif sampai sisanya = 0. Sisa-sisa pembagian membentuk jawaban, yaitu sisa yang pertama akan menjadi least significant bit (LSB) dan sisa yang terakhir menjadi most significant bit (MSB).

§ Contoh: Konversi 17910 ke oktal: § 179 / 8 = 22 sisa 3 (LSB) § 22 / 8 = 2 sisa 6 § 6 / 8 = 0 sisa 2 (MSB) § § § 17910 = 2638 MSB LSB

Konversi Bilangan Desimal ke Hexadesimal § Konversi bilangan desimal bulat ke bilangan hexadesimal: Gunakan pembagian dgn 16 secara suksesif sampai sisanya = 0. Sisasisa pembagian membentuk jawaban, yaitu sisa yang pertama akan menjadi least significant bit (LSB) dan sisa yang terakhir menjadi most significant bit (MSB).

§ Contoh: Konversi 17910 ke hexadesimal: 179 / 16 = 11 sisa 3 (LSB) 11 / 16 = 0 sisa 11 (MSB) (dalam bilangan hexadesimal berarti B) 17910 = B 316 MSB LSB

Sistem Bilangan Biner § Basis 2 § Bilangan : 0, 1

Lanjutan Sistem Bilangan Biner. . Contoh : 1110 bilangan desimalnya adalah : (1 * 23) + (1 * 22) + (1 * 21) + (0 * 20) = 8 + 4 + 2 + 0 = 14 10 110111 bilangan desimalnya adalah : (1 * 25) + (1 * 24) + (0 * 23) + (1 * 22) + (1 * 21) + (1 * 20) = 32 + 16 + 0 + 4 + 2 + 1 = 55 10

Lanjutan Sistem Bilangan Biner… -Konversikan bilangan desimal 50 ke bilangan biner dilakukan dengan cara sebagai berikut : 50 / 2 25 / 2 12 / 2 6/2 3/2 1/2 = 25 sisa 0 = 12 sisa 1 = 6 sisa 0 = 3 sisa 0 = 1 sisa 1 = 0 sisa 1 5010 = 1 1 0 0 1 02 LSB MSB

Sistem Bilangan Oktal Bilangan oktal merupakan bilangan berbasis 8 jadi bilangan ini terdiri dari angka 0, 1, 2, 3, 4, 5, 6, 7

Lanjutan Sistem Bilangan Oktal… Contoh : 355 bilangan oktal ke desimal : 355 oktal atau 3558 = (3 * 82) + (5 * 81) + (5 * 80) = 192 + 40 + 5 = 237 Desimal atau 23710 204 bilangan oktal ke desimal : 204 oktal atau 2048 = (2 * 82) + (0 * 81) + (4 * 80) = 128 + 0 + 4 = 132 Desimal atau 13210

Konversi Bilangan Desimal ke Oktal § Konversi bilangan desimal bulat ke bilangan oktal: Gunakan pembagian dgn 8 secara suksesif sampai sisanya = 0. Sisasisa pembagian membentuk jawaban, yaitu sisa yang pertama akan menjadi least significant bit (LSB) dan sisa yang terakhir menjadi most significant bit (MSB). § Konversikan 96 desimal menjadi bilangan oktal : 96 / 8 = 12 sisa 0 12 / 8 = 1 sisa 4 hasil : 140 oktal 1 / 8 = 0 sisa 1 9610 hasilnya ke oktal : 1408

Konversi Bilangan Biner ke Oktal Untuk mengkonversi bilangan biner ke bilangan oktal, lakukan pengelompokan 3 digit bilangan biner dari posisi LSB sampai ke MSB Konversikan 1011101 bilangan biner ke bilangan oktal : 1 011 1011101 = 1 3 5 Dengan demikian : 10111012 = 1358

§ Contoh: konversikan 101100112 ke bilangan oktal Jawab : 10 110 011 2 6 3 Jadi 101100112 = 2638

Sistem Bilangan Hexa Desimal Bilangan Hexadesimal merupakan bilangan berbasis 16 jadi bilangan ini terdiri dari angka 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 dan A, B, C, D, E, F

Lanjutan Sistem Bilangan Hexa Desimal…

Lanjutan Sistem Bilangan Hexa Desimal. . Konversi bilangan desimal bulat ke bilangan hexadesimal: Gunakan pembagian dgn 16 secara suksesif sampai sisanya = 0. Sisa-sisa pembagian membentuk jawaban, yaitu sisa yang pertama akan menjadi least significant bit (LSB) dan sisa yang terakhir menjadi most significant bit (MSB). Konversikan bilangan desimal 400 menjadi bilangan hexadesimal : 400 / 16 = 25 sisa 0 25 / 16 = 1 sisa 9 1 / 16 = 0 sisa 1 40010 hasil nya adalah : 19016

Konversi Bilangan Biner ke Hexa Desimal Untuk mengkonversi bilangan biner ke bilangan oktal, lakukan pengelompokan 3 digit bilangan biner dari posisi LSB sampai ke MSB Konversikan 1101101 (biner) menjadi bilangan hexa desimal 0110 1101101 = 6 11011012 = 6 CD 16 C D