SISTEM BERBASIS ATURAN FUZZY Pengertian Disebut juga sistem

SISTEM BERBASIS ATURAN FUZZY

Pengertian • Disebut juga sistem inferensi fuzzy • Proses memformulasikan pemetaan dari input yang diberikan ke sebuah output dengan menggunakan logika fuzzy. • Dasar bagaimana sebuah keputusan dibuat • Melibatkan : fungsi keanggotaan, operasi logika dan aturan if-then

KOMPONEN UTAMA • Fuzzification ▫ Mengubah crisp input menjadi fuzzy input • Inference ▫ Melakukan penalaran menggunakan fuzzy input dan fuzzy rules yang telah ditentukan sehingga menghasilkan fuzzy output ▫ Ada 3 hal : �aplikasi operator fuzzy pada anteseden �implikasi dari anteseden ke konsekuen �aggregasi output • Defuzzification ▫ Mengubah fuzzy output menjadi crisp value berdasarkan fungsi keanggotaan yang telah ditentukan

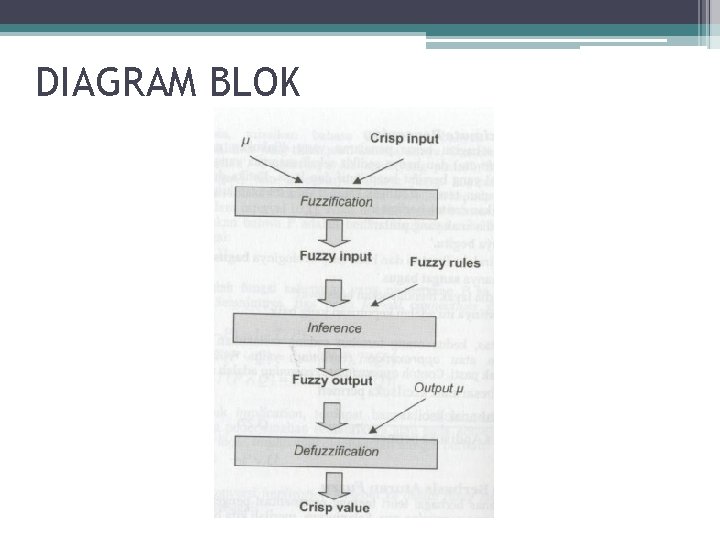
DIAGRAM BLOK

Fuzzifikasi Variabel Input • Tahap fuzzifikasi adalah ▫ tahap untuk mengolah input yang diberikan ▫ menentukan derajat keanggotaannya (antara 0 sampai 1) berdasarkan fungsi keanggotaan himpunan fuzzynya • Contoh penerapan fuzzifikasi. .

Fuzzifikasi Variabel Input Contoh penerapan fuzzifikasi pada dua buah input x 1 dan y 1 • input X memiliki tiga fungsi keanggotaan (A 1, A 2, dan A 3) • Pada saat menerima input x 1, akan dievaluasi nilai input x 1 ke dalam sebuah nilai di setiap fungsi keanggotaan : µ(x=A 1) = 0. 5, µ(x=A 2) = 0. 2, dan µ(x=A 3) = 0 • hasil evaluasi nilai input y 1 adalah µ(y=B 1) = … dan µ(y=B 2) = …

INFERENSI FUZZY : TIPE • Ada beberapa : Mamdani, Sugeno dan Tsukamoto • Inferensi tipe Mamdani ▫ menghasilkan fungsi keanggotaan outputnya sebagai himpunan fuzzy. ▫ Sesudah proses aggregasi, terdapat himpunan fuzzy untuk masing-masing variabel output yang memerlukan defuzzifikasi (penegasan). • Inferensi tipe Sugeno ▫ digunakan untuk memodelkan sistem inferensi yang fungsi keanggotaan outputnya berupa linier atau konstanta.

INFERENSI FUZZY : TIPE • Inferensi tipe Tsukamoto ▫ setiap konsekuen pada aturan yang berbentuk ifthen harus direpresentasikan dengan himpunan fuzzy yang memiliki fungsi keanggotaan yang monoton ▫ output hasil inferensi akan diberikan dalam bentuk nilai crisp berdasarkan α-predikat (fire strength)

INFERENCE : Aplikasi Operator Fuzzy pada Anteseden • Hasil fuzzifikasi tiap bagian diaplikasikan sebagai anteseden dari aturan fuzzy. • Anteseden lebih dari satu bagian operator fuzzy diaplikasikan untuk mendapatkan nilai tunggal yang merepresentasikan hasil anteseden dari aturan tersebut

INFERENCE : Aplikasi Operator Fuzzy pada Anteseden Operator fuzzy : • Operator fuzzy OR µA(x)∪B(x) = max [µA(x), µB(x)], digunakan untuk operasi fuzzy gabungan • Operator fuzzy AND µA(x)∩B(x) = min [µA(x), µB(x)], digunakan untuk operasi fuzzy irisan • Operator fuzzy NOT ¬µA(x) = [1 -µA(x)], digunakan untuk operasi fuzzy komplemen.

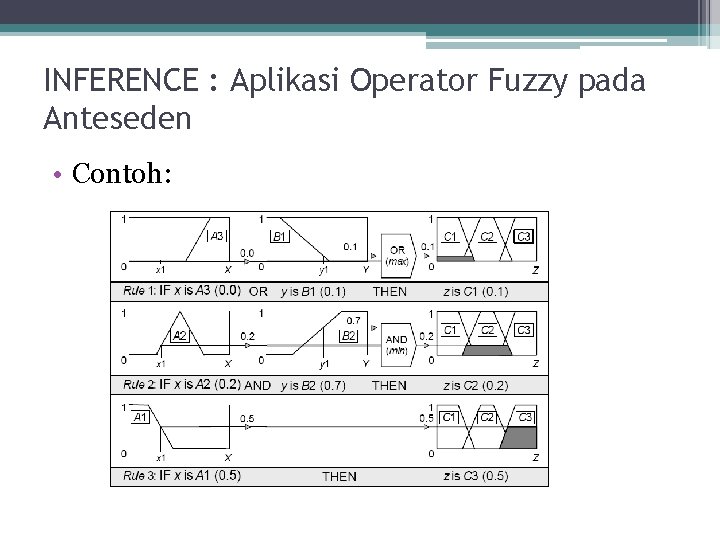
INFERENCE : Aplikasi Operator Fuzzy pada Anteseden • Contoh:

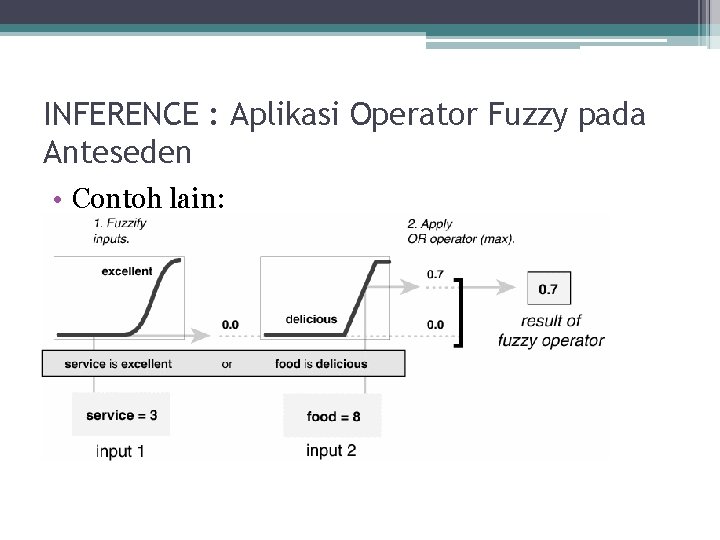
INFERENCE : Aplikasi Operator Fuzzy pada Anteseden • Contoh lain:

INFERENCE : Implikasi dari Anteseden ke Konsekuen • Input pada proses implikasi adalah nilai tunggal yang diberikan oleh anteseden, dan outputnya berupa himpunan fuzzy. • Implikasi ini diimplementasikan pada masing aturan.

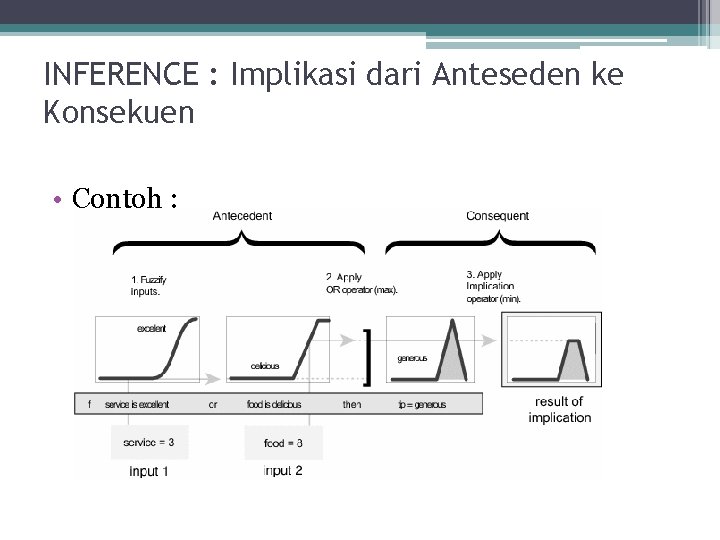
INFERENCE : Implikasi dari Anteseden ke Konsekuen • Contoh :

INFERENCE : Aggregrasi Output • Proses dimana himpunan-himpunan fuzzy yang merepresentasikan output dari tiap-tiap aturan dikombinasikan dalam sebuah himpunan fuzzy tunggal. ▫ Input sederetan output hasil proses implikasi, ▫ output sebuah himpunan fuzzy untuk masing-masing variabel output. • Metode aggregasi ada 3 macam, ▫ metode max (maximum), ▫ metode probor (probabilistic or) ▫ metode sum (the sum of each rules output set).

AGGREGASI OUTPUT Metode Max • Langkah-langkah: ▫ Mengambil nilai maksimum aturan untuk memodifikasi daerah fuzzy ▫ Mengaplikasikannya ke output dengan menggunakan operator OR

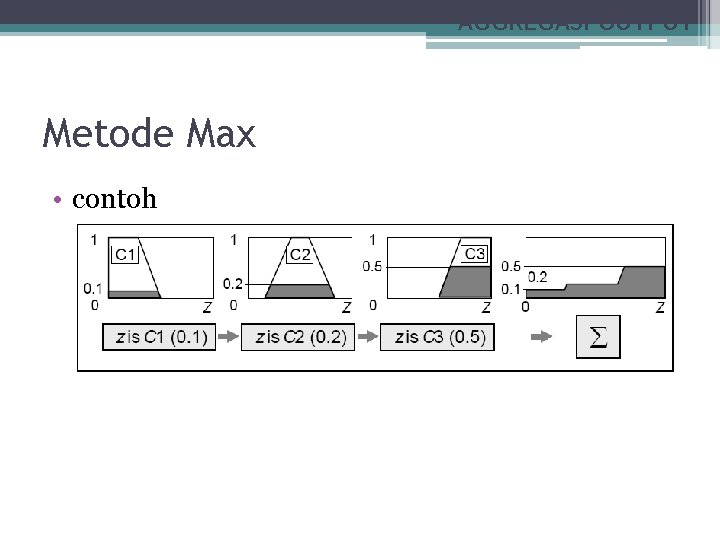
AGGREGASI OUTPUT Metode Max • contoh

AGGREGASI OUTPUT Metode Sum • Menjumlah semua output daerah fuzzy • Rumus umum : μsf [xi] ← min (1, μsf [xi] + μkf [xi]) dengan : μsf [xi] : Nilai keanggotaan solusi fuzzy sampai aturan ke-i μkf [xi] : Nilai keanggotaan konsekuen fuzzy aturan ke-i • Bagaimana hasilnya jika contoh dalam Metode Max diganti dengan Metode Sum?

AGGREGASI OUTPUT Metode Probor • Solusi didapat dengan melakukan product terhadap semua output daerah fuzzy • INGAT : Operator Product !!

INGAT KEMBALI!!! OPERATOR PRODUCT • Rumus yang digunakan : ▫ Interseksi ▫ Union : μ A∩B = μ A[x] * μ B[y] : μ A∪B = (μ A[x] +μ B[y]) - (μ A[x] * μ B[x]) • Contoh: ▫ Diberikan aturan sbb: IF service is excellent PRODUCT. OR food is delicious THEN tip is generous ▫ Diberi input service =3 dan food = 8 sehingga derajat keanggotaan untuk μ excellent[x] = 0, 0 dan μ delicious[y] = 0, 7.

OPERATOR PRODUCT • Nilai keanggotaan fuzzy untuk predikat aturan tersebut adalah A = (μ excellent [x] +μ delicious [y]) - (μ excellent [x] * μ delicious [y]) = (0, 0 + 0, 7) – (0, 0 * 0, 7) = 0, 7

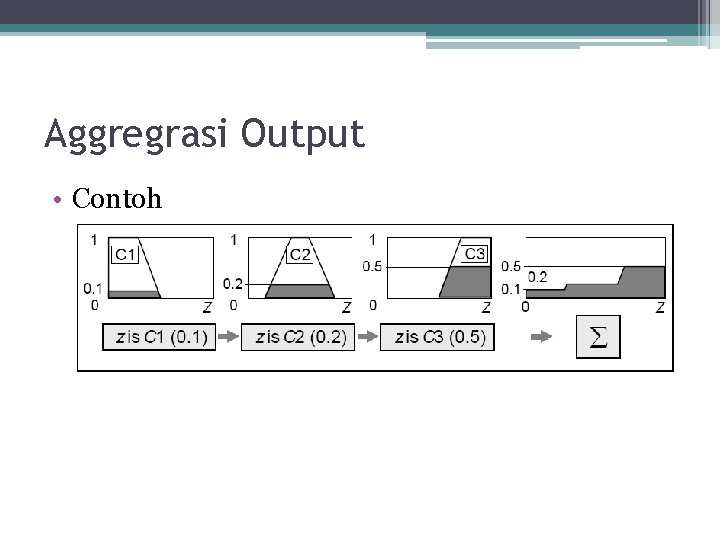
Aggregrasi Output • Contoh

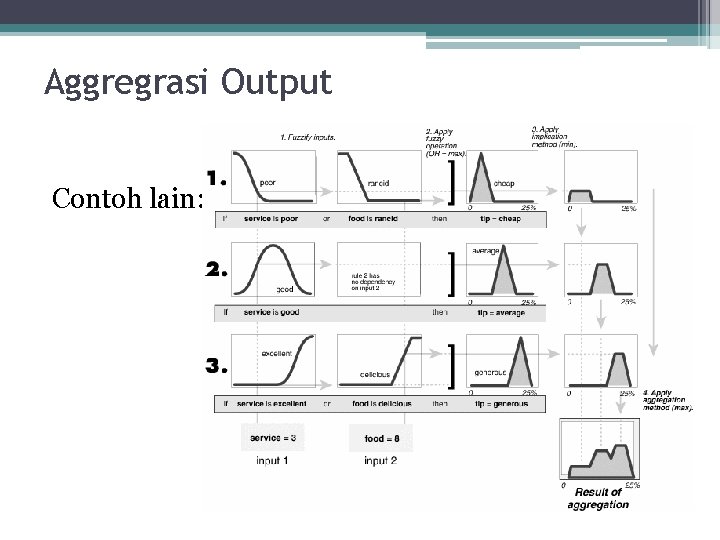
Aggregrasi Output Contoh lain:

Defuzzifikasi • Input suatu himpunan fuzzy hasil aggregasi • output suatu b ilangan (nilai crisp) pada domain himpunan fuzzy tersebut • Metode defuzzifikasi yang sering digunakan adalah metode centroid. ▫ Dalam metode ini solusi crisp diperoleh dengan cara mengambil titik pusat daerah fuzzy. • Metode lain : ▫ ▫ metode bisektor metode mean of maximum (MOM) metode largest of maximum (LOM) metode smallest of maximum (SOM).

Metode defuzzifikasi • Metode Centroid ▫ Solusi dipilih dengan mengambil titik pusat daerah fuzzy atau ▫ Keuntungan : �Mudah dihitung �Nilai defuzzy akan bergerak secara halus

Metode defuzzifikasi • Metode bisektor ▫ Mengambil nilai pada domain fuzzy yang memiliki nilai keanggotaan separo dari jumlah total nilai keanggotaan pada daerah fuzzy ▫ Rumus umum : zp sedemikian sehingga • Metode mean of maximum (MOM) ▫ Mengambil nilai rata-rata domain yang memiliki nilai keanggotaan maksimum

Metode defuzzifikasi • Metode largest of maximum (LOM) ▫ Mengambil nilai terbesar dari domain yang memiliki nilai keanggotaan maksimum ▫ Disebut juga Height method ▫ Hanya bisa dipakai untuk fungsi keanggotaan yang memiliki derajat keanggotaan 1 dan lainnya 0 untuk suatu nilai crisp singleton • Metode smallest of maximum (SOM) ▫ Mengambil nilai terkecil domain yang memiliki nilai keanggotaan maksimum

Metode defuzzifikasi • Metode defuzzifikasi pada komposisi aturan Sugeno ▫ Metode weight average: �Mengambil nilai rata-rata terbobot �y adalah nilai crisp dan µ(y) adalah derajat keanggotaan dari y

Defuzzifikasi • Contoh

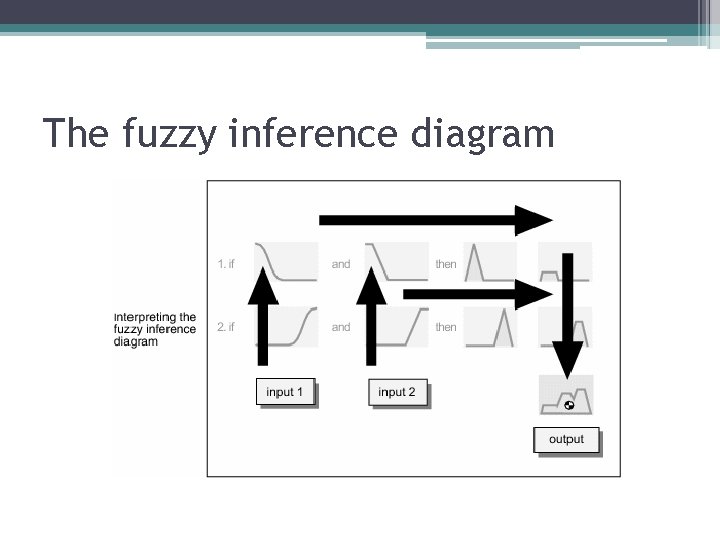
The fuzzy inference diagram

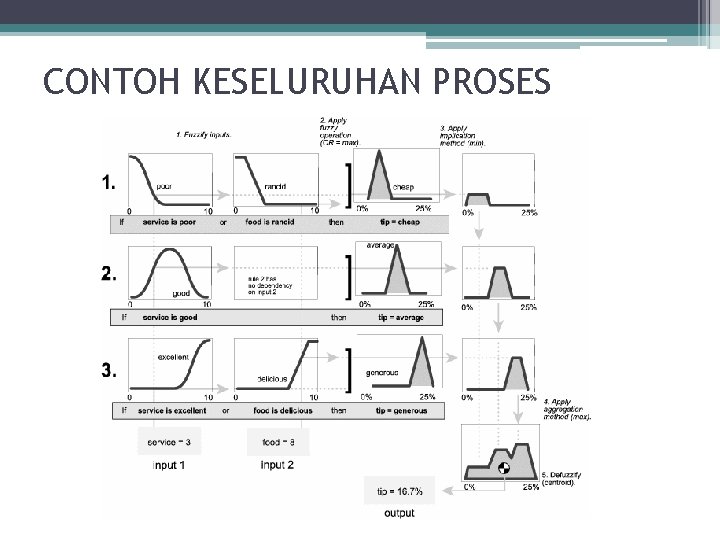
CONTOH KESELURUHAN PROSES

STUDI KASUS : Sistem Kontrol Penyiram Air • Suatu sistem akan dibangun untuk mengontrol alat penyiram air. Input dari sistem tersebut adalah suhu udara (0 C) dan kelembaban tanah (%). Sedangkan output yang diinginkan adalah durasi penyiraman (dalam satuan menit ). • Jika nilai yang diterima oleh sensor suhu adalah 370 C dan nilai yang diterima sensor kelembaban adalah 12 %, berapa lama durasi penyiraman yang harus dilakukan dengan menggunakan metode Mamdani dan meode Sugeno?

Asumsi • Fungsi keanggotaan Suhu Udara

Asumsi • Fungsi keanggotaan Kelembaban

Asumsi • Fungsi keanggotaan Durasi Penyiraman (Mamdani)

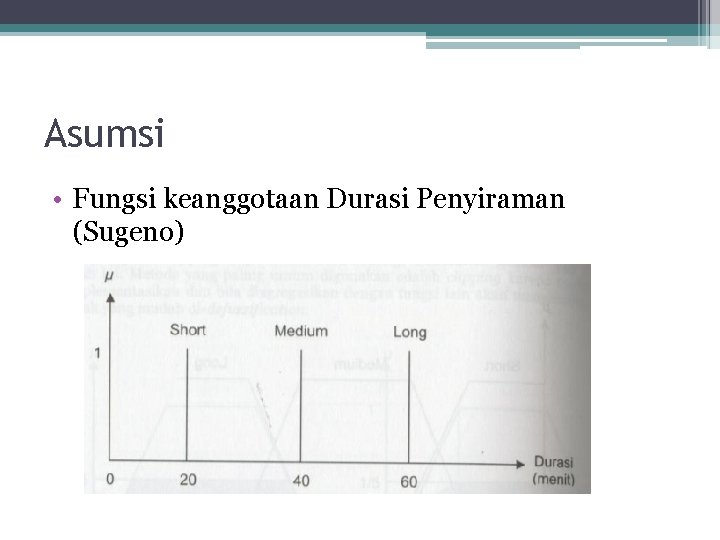
Asumsi • Fungsi keanggotaan Durasi Penyiraman (Sugeno)

Asumsi • Aturan yang diberikan

Penyelesaian • Fuzzifikasi var input ▫ Sudah jelas • Proses inferensi ▫ If Suhu is Warm (2/3) And Kelembaban is Dry (4/5) Then Durasi is Long (2/3) ▫ If Suhu is Warm (2/3) And Kelembaban is Moist (1/5) Then Durasi is Medium (1/5) ▫ If Suhu is Hot (1/3) And Kelembaban is Dry (4/5) Then Durasi is Long (1/3) ▫ If Suhu is Hot(1/3) And Kelembaban is Moist (1/5) Then Durasi is Medium (1/5)

Penyelesaian • Hasil Aggregasi Metode Mamdani

Penyelesaian • Defuzzifikasi centroid ▫ Untuk mempermudah perhitungan menggunakan rumus untuk yang diskrit ▫ Menentukan titik sebarang pada daerah hasil aggregat (mis: 24, 28, 32, 36, 40, 48, 60, 70, 80, 90)

Penyelesaian

Penyelesaian • Hasil aggregasi metode Sugeno

Penyelesaian • Defuzzifikasi ▫ Height method Durasi Penyiraman = 60 menit ▫ Weighted Average