Singular Value Decomposition and ItemBased Collaborative Filtering for

Singular Value Decomposition and Item-Based Collaborative Filtering for Netflix Prize Presentation by Tingda Lu at the Saturday Research meeting 10_23_10 enhanced (with audio added) by William perrizo Computer Science North Dakota State University Fargo, ND 58108 USA

Agenda n n Singular Value Decomposition Item-based P-Tree CF algorithm Similarity measurements Experimental results Recommendation System n n n analyzes customer’s purchase history identifies customer’s preference recommends most likely purchases increases customer satisfaction leads to business success SVD amazon. com and Netflix n SVD is an important factorization of a n n rectangular real or matrix, with apps in signal processing and statistics SVD proposed in Netflix by Simon Funk SVD, mathematically, looks nothing like this but engineers, over many years have boiled the technique down into very simple versions (such as this one) for their quick and effective use

SVD n n n n features --> movies --> features --> What about creating and optimizing (with back propagation) a custom matrix for each prediction we have to make? - i. e. , in movievote. C or user-vote. C. The call from mpp-user-C to e. g. , movie-vote. C sends M, U, sup. M, sup. U. *** In movie-vote [or user-vote] before entering nested loop (outer Voter. Loop, inner Dim. Loop), train optimal VT and N matrixes for that vote only (so number of features could be raised substantially since [pruned] sup. M and sup. U are << 17, 000 and 500, 000). users --> n User’s rate movies with user preferences about various features of the movie. Features can be anything you want them to be (or nothing! randomly constructed!). In fact, it is typical to start with a fix number of meaningless features populated with random values, then back propagate to "improve" those values until some satisfaction level is reached (in terms of the RMSE). This back propagation is identical to that of the back prop of Neural Networks. Tingda found 30 features too small and 100 right (200 was too time consuming). Arijit: Go to Netflix site for feature ideas (meaningful features ought to be better? )

SVD training n n Parameters: learning rate and lambda Tune the parameters to minimize error n Collaborative Filtering (CF) alg is widely used in recommendation systems n User-based CF algorithm is limited because of its computation complexity n Movie-based (Item-based) CF has less scalability concerns sim is any simmilarity function. The only req. is /* Movie-based PTree CF*/ that sim(i. i) >= sim(i, j). In movie-vote. C one could backpropagate train VT and N (see *** on previous PTree. load_binary(); slide) anew for each call from mpp-user. C to movie -vote. C and thereby allow a large number of // Calculate the similarity features (much higher accuracy? ) because VT and N while i in I { are much smaller than UT and M while j in I { simi, j = sim(PTree[i], Ptree[j]); } } // Get the top K nearest neighbors to item i pt=Ptree. get_items(u); sort(pt. begin(), pt. end(), simi, pt. get_index()); // Prediction of rating on item i by user u sum = 0. 0, weight = 0. 0; for (j=0; j<K; ++j) { sum += ru, pt[j] * simi, pt[j]; weight += simi, pt[j]; } pred = sum/weight Here Closed Nearest Neighbor methods should improve the result! If the similarity is simple enough to allow the calculation through PTrees, then closed K Nearest Neighbor will be both faster and more accurate.

Similarities (correlations) n Cosine based n Pearson correlation Adjusted Cosine SVD item-feature or Tingda Lu similarity? or combining Pearson and Adj Cosine: * i i j j

Similarity Correction n n Two items are not similar if only a few customers purchased or rated both Co-support is included in item similarity Prediction Weighted Average Item Effects RMSE Neighbor Size Cosine Pearson Adj. Cos SVD IF K=10 1. 0742 1. 0092 0. 9786 0. 9865 K=20 1. 0629 1. 0006 0. 9685 0. 9900 K=30 1. 0602 1. 0019 0. 9666 0. 9972 K=40 1. 0592 1. 0043 0. 9960 1. 0031 K=50 1. 0589 1. 0064 0. 9658 1. 0078 Adj Cosine similarity gets much lower RMSE The reason lies in the fact that other algorithms do not exclude the user rating variance Adjusted Cosine algorithm discards the user variance hence gets better prediction accuracy

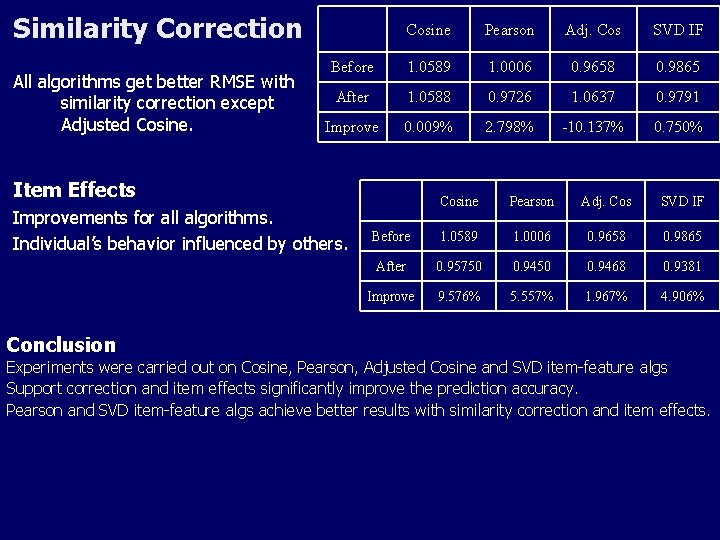
Similarity Correction All algorithms get better RMSE with similarity correction except Adjusted Cosine Pearson Adj. Cos SVD IF Before 1. 0589 1. 0006 0. 9658 0. 9865 After 1. 0588 0. 9726 1. 0637 0. 9791 Improve 0. 009% 2. 798% -10. 137% 0. 750% Item Effects Improvements for all algorithms. Individual’s behavior influenced by others. Cosine Pearson Adj. Cos SVD IF Before 1. 0589 1. 0006 0. 9658 0. 9865 After 0. 95750 0. 9468 0. 9381 Improve 9. 576% 5. 557% 1. 967% 4. 906% Conclusion Experiments were carried out on Cosine, Pearson, Adjusted Cosine and SVD item-feature algs Support correction and item effects significantly improve the prediction accuracy. Pearson and SVD item-feature algs achieve better results with similarity correction and item effects.

10_23_10 Saturday notes (by Mohammad) Participants: Mohammad, Arjun, Arijit, Using Skype – Tingda and Prakash. Tingda Lu: “Singular Value Decomposition and item-based collaborative filtering for Netflix prize”. As Tingda went through the slides, the group members discussed various issues. Here are some key points of the discussions In the 5 th slide, Tingda showed two matrices U and M. Matrix UT contains the users in rows and features in the columns. So there would be 500, 000 rows in the matrix (as there are half a million users in the Netflix problem) but number of features is not known (as it is not described in the problem). As Tingda mentioned, you can take as many features as you wish but larger number would give you good result. The value of these features might be randomly filled but they will converge to some values by neural network back propagation. As Tingda found 10 to 30 features are too small, 40 – 60 still not large enough and 100 is good enough. M is the movie matrix where rows represent the features and columns represent the movies. So there are 100 features and 17, 000 movies. So it’s a 100 x 17000 matrix – same thing goes for the features. Arijit suggested that we may go the Netflix’s website to see what the features they use to describe their movies are and we may use those features. In slide no 8, an algorithm is shown for “Item based PTree CF”. The alg 1 st calculates similarity between items in the item set I. Here a long discussion took place to choose the similarity function: – Tingda gave 4 similarity fctns; cosine, pearson, adjusted cosine and SVD item feature (shown in slide 9, 10). – Dr. Perrizo's similarity is Sim(i, j) = a positive real number following the property that Sim(i, i) >= Sim(i, j). – Dr. Perrizo made a suggestion of combining the Pearson and Adjusted cosine similarity function as follows: In 2 nd part, K nearest nbrs are computed. Dr. P suggested to use Closed KNN. I. e. , consider all nbrs same distance as kth Dr. P. : use Sum of Cor (ui, uj), not Nij Then Dr. P. : Use these similarities in use-vote. C and movie-vote. C and get ‘Pruned Training Set Support’ (PTSS) values, which will be used by mpp-user. C to make the final prediction (? ) More features -> more accuracy: In 1, if we include more features that will give us more accuracy in prediction. But we already have too many rows in user matrix (half a million). And we need to train the matrix using back prop (very time consuming). So don’t train matrices before pruning seriously like 10 users so that you can increase number of features. Make code generic (not specific to Netflix problem) so that the code may be used in e. g. , satellite imagery – Land. Sat 5? ). 0 rating is not really 0 in Netflix problem should be removed in generic code as 0 may be a valid rating in other problem. Tingda used similarity correction. E. g. , he didn’t use 2 items ( or movies) similar if only a few number of users rated both. Tingda's formula: Log(Nij)*Sim(I, j) Dr. Perrizo suggest to use Sum of Cor (ui, uj) instead of Nij