SingleSide Band SSB Modulation DSBSC as well as

Single-Side Band (SSB) Modulation • DSBSC (as well as AM) occupies double the bandwidth of the baseband signal, although the two sides carry the same information. • Why not send only one side, the upper or the lower? • Modulation: similar to DSBSC. Only change the settings of the BPF (center frequency, bandwidth). • Demodulation: similar to DSBSC (coherent)

SSB Representation How would we represent the SSB signal in the time domain? g. USB(t) = ? g. LSB(t) = ?

Time-Domain Representation of SSB (1/2) M( ) = M+( ) + M-( ) Let m+(t)↔M+( ) and m-(t)↔M( ) Then: m(t) = m+(t) + m-(t) [linearity] Because M+( ), M-( ) are not even m+(t), m-(t) are complex. Since their sum is real they must be conjugates. m+(t) = ½ [m(t) + j mh(t)] m-(t) = ½ [m(t) - j mh(t)] What is mh(t) ?

Time-Domain Representation of SSB (2/2) M( ) = M+( ) + M-( ) M+( ) = M( )u( ); M-( ) = M( )u(- ) sgn( )=2 u( ) -1 u( )= ½ + ½ sgn( ); u(- ) = ½ -½ sgn( ) M+( ) = ½[ M( ) + M( )sgn( )] M-( ) = ½ [M( ) - M( )sgn( )] Comparing to: m+(t) = ½ [m(t) + j mh(t)] ↔ ½ [M( ) + j Mh( )] m-(t) = ½ [m(t) - j mh(t)] ↔ ½ [M( ) - j Mh( )] We find Mh( ) = - j M( )∙sgn( ) where mh(t)↔Mh( )

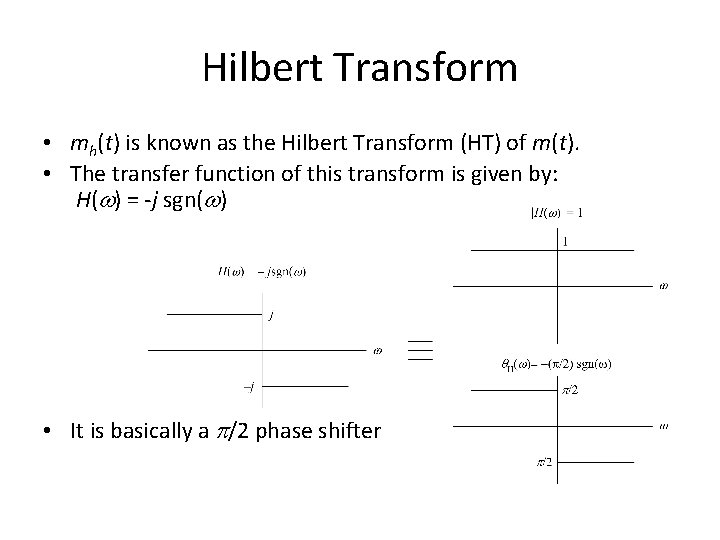
Hilbert Transform • mh(t) is known as the Hilbert Transform (HT) of m(t). • The transfer function of this transform is given by: H( ) = -j sgn( ) • It is basically a p/2 phase shifter

Hilbert Transform of cos( ct) ↔ p [d( – c) + d( + c)] HT[cos( ct)] ↔ -j sgn( ) p [d( – c) + d( + c)] = j sgn( ) p [-d( – c) - d( + c)] = j p [-d( – c) + d( + c)] = j p [d( + c) - d( - c)] ↔ sin( ct) Which is expected since: cos( ct-p/2) = sin( ct)

Time-Domain Operation for Hilbert Transformation For Hilbert Transformation H( ) = -j sgn( ). What is h(t)? sgn(t) ↔ 2/(j ) [From FT table] 2/(jt) ↔ 2 p sgn(- ) [symmetry] 1/(p t) ↔ -j sgn( ) Since Mh( ) = - j M( )∙sgn( ) = H( ) ∙ M( ) Then

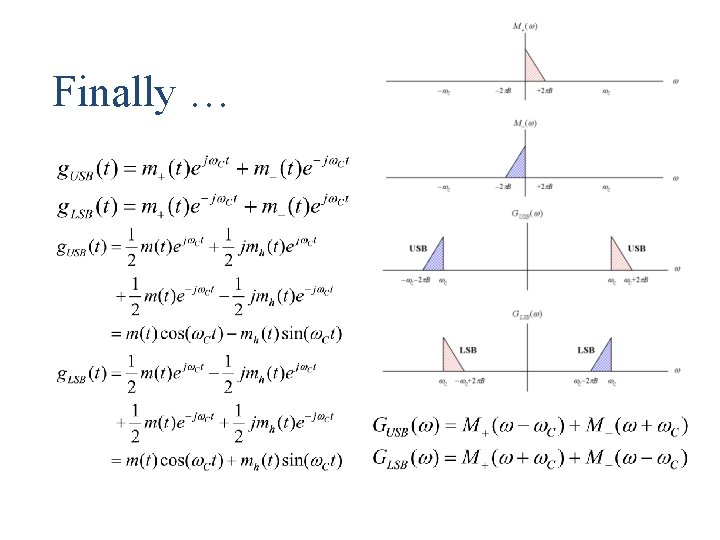
Finally …

Generation of SSB • Selective Filtering Method Realization based on spectrum analysis • Phase-Shift Method Realization based on time-domain expression of the modulated signal

Generating SSB Signals: The Filter Method • The filter method is the simplest and most widely used method of generating SSB signals. • The modulating signal is applied to the audio amplifier. • The amplifier’s output is fed to one input of a balanced modulator. • A crystal oscillator provides the carrier signal which is also applied to the balanced modulator.

The Filter Method • The output of the balanced modulator is a double- sideband (DSB) signal. • An SSB signal is produced by passing the DSB signal through a highly selective bandpass filter. • With the filter method, it is necessary to select either the upper or the lower sideband.

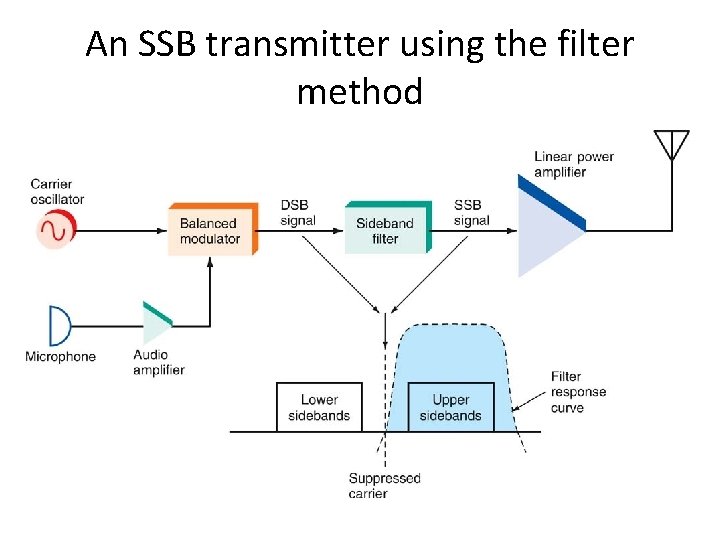
An SSB transmitter using the filter method

Phase Shift Method • The phasing method of SSB generation uses a phase-shift technique that causes one of the sidebands to be canceled out. • The phasing method uses two balanced modulators which eliminate the carrier. • The carrier oscillator is applied to the upper balanced modulator along with the modulating signal.

Phase Shift Method • The carrier and modulating signals are both shifted in phase by 90 degrees and applied to another balanced modulator. • Phase-shifting causes one sideband to be canceled out when the two modulator outputs are added together.

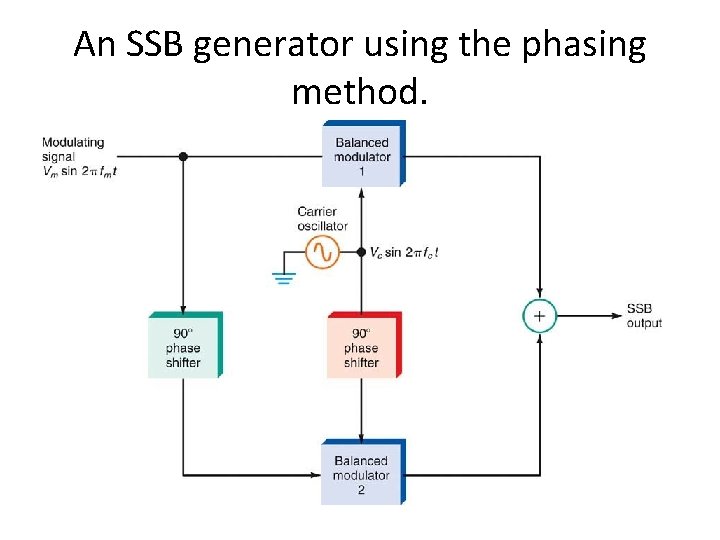
An SSB generator using the phasing method.

DSB and SSB Demodulation • To recover the intelligence in a DSB or SSB signal, the carrier that was suppressed at the receiver must be reinserted. • A product detector is a balanced modulator used in a receiver to recover the modulating signal. • Any balanced modulator can be used as a product detector to demodulate SSB signals.

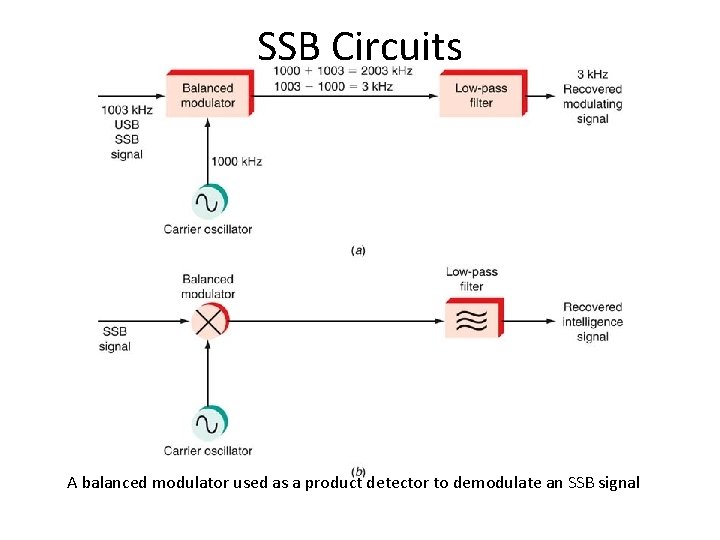
SSB Circuits A balanced modulator used as a product detector to demodulate an SSB signal

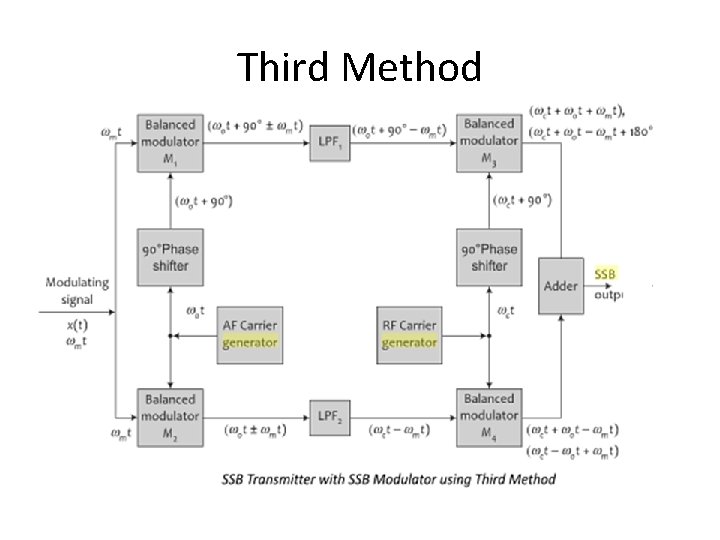
Third Method

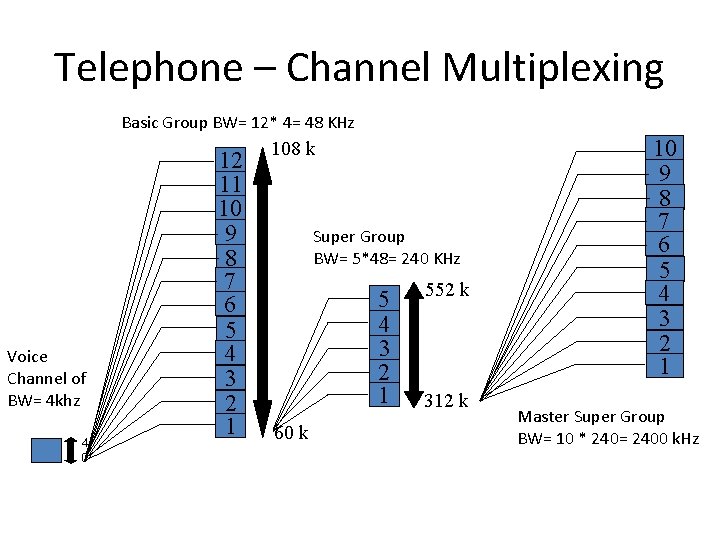
Telephone – Channel Multiplexing Basic Group BW= 12* 4= 48 KHz Voice Channel of BW= 4 khz 4 0 12 11 10 9 8 7 6 5 4 3 2 1 108 k Super Group BW= 5*48= 240 KHz 5 4 3 2 1 60 k 552 k 312 k 10 9 8 7 6 5 4 3 2 1 Master Super Group BW= 10 * 240= 2400 k. Hz