SingleServer Queue Model 1 MODELING AND SIMULATION CS

Single-Server Queue Model 1 MODELING AND SIMULATION CS 313

Specification model 2 � The following variables, illustrated in Figure 1. 2. 2, provide the basis for moving from a conceptual model to a specification model. At their arrival to the service node, jobs are indexed by i = 1, 2, 3, … For each job there are six associated time variables.

Specification model (Arrivals) 3 � Rather than specifying the arrival times a 1, a 2, … explicitly, in some discrete-event simulation applications it is preferable to specify the arrival times r 1, r 2, …, thereby defining the arrival times implicitly, as shown:

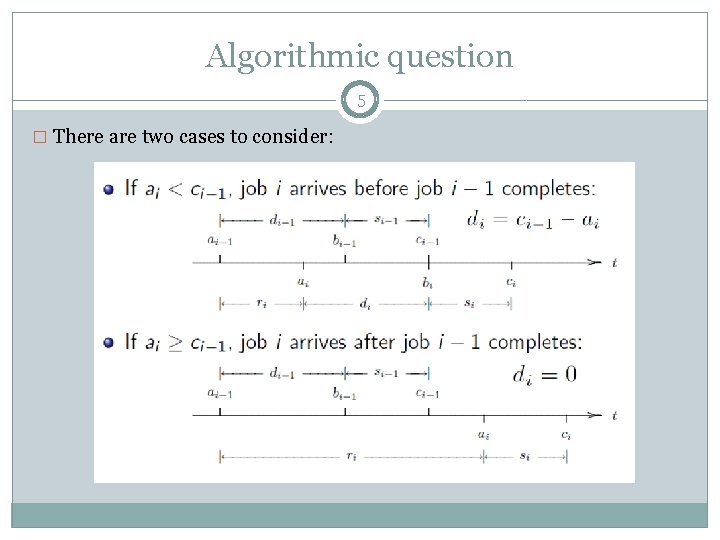
Algorithmic question 4 � Given a knowledge of the arrival times a 1, a 2, . . . (or, equivalently, the interarrival times r 1, r 2, . . . ), the associated service times s 1, s 2, . . . , and the queue discipline, how can the delay times d 1, d 2, . . . be computed? � For some queue disciplines this question is more difficult to answer than for others. If the queue discipline is FIFO, however, then the answer is particularly simple. � If the queue discipline is FIFO, di is determined by when ai occurs relative to ci− 1.

Algorithmic question 5 � There are two cases to consider:

Algorithm 6 � The key point in algorithm development is that if the queue discipline is FIFO, then the truth of the expression ai < ci-1 determines whether or not job i will experience a delay. � An equation can be written for the delay that depends on the interarrival and service times only. That is:

Algorithm 7 � Algorithm 1. 2. 1 � If the arrival times a 1, a 2, … and service times s 1, s 2, … are known, and if the server is initially idle, then this algorithm computes the delays d 1, d 2, … in a single-server FIFO service node with infinite capacity.

Algorithm 8 � Algorithm 1. 2. 1 � The Get. Arrival and Get. Service procedures read the next arrival and service time from a file. � Example: Algorithm 1. 2. 1 used to process n = 10 jobs

Output statistics 9 � The purpose of simulation is insight gained by looking at statistics. � The importance of various statistics varies on perspective: Job perspective: wait time is most important Manager perspective: utilization is critical � Statistics are broken down into two categories: Job-averaged statistics Time-averaged statistics

Job-Averaged Statistics 10 � Job-averaged statistics: computed via typical arithmetic mean Average interarrival time: The reciprocal of the average interarrival time, Average service time: The reciprocal of the average service time, , is the arrival rate; , is the service rate.

Output statistics 11 � For the 10 jobs in the previous example: Average interarrival time is: � The server is not quite able to process jobs at the rate they arrive on average.

Job-Averaged statistics 12 � The average delay and average wait are defined as: � Recall wi = di + si for all i � The point here is that it is sufficient to compute any two of the statistics . . The third statistic can then be computed from the other two, if appropriate.

Job-Averaged statistics 13 � From the data in the previous example: � Therefore: � Recall verification is one (difficult) step of model development � Consistency check: used to verify that a simulation satisfies known equations:

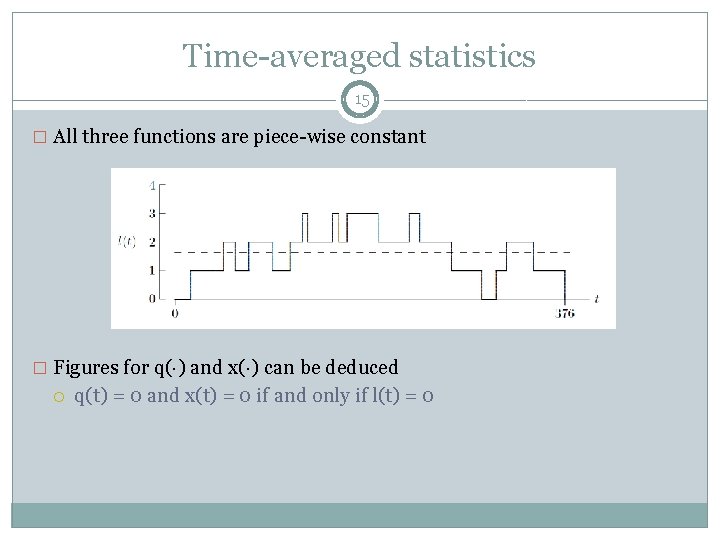
Time-Averaged statistics 14 � Time-averaged statistics: defined by area under a curve (integration) � For SSQ, need three additional functions: l (t): number of jobs in the service node at time t q(t): number of jobs in the queue at time t x(t): number of jobs in service at time t. � By definition, l (t) = q(t) + x(t) l (t) = 0, 1, 2, . . . q(t) = 0, 1, 2, . . . x(t) = 0, 1

Time-averaged statistics 15 � All three functions are piece-wise constant � Figures for q(·) and x(·) can be deduced q(t) = 0 and x(t) = 0 if and only if l(t) = 0

Time-Averaged statistics 16 � Over the time interval (0, T ): � Since l (t) = q(t) + x(t) for all t > 0 � Sufficient to calculate any two of

Time-Averaged statistics 17 � The average of numerous random observations (samples) of the number in the service node should be close to � Same holds for � Server utilization: time-averaged number in service � also represents the probability the server is busy.