Single species population growth models HW 1 Recreate

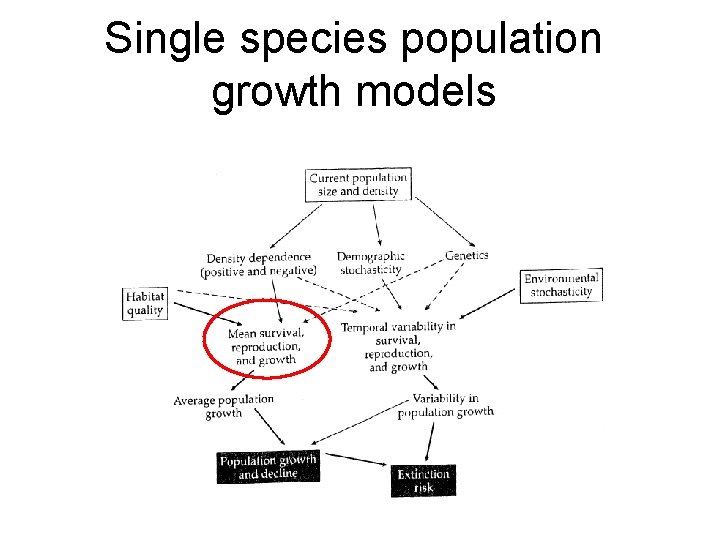
Single species population growth models

HW 1: Recreate Deterministic Matrix from Literature • Quick overview – Species/system – Elasticity/Sensitivity (which classes? ) – Issues?

Matrix population models

4 x 4 size-structured matrix (also called Lefkovitch matrix) Pij=probability of growing from one size to the next or remaining the same size (need subscripts to denote new possibilities) F=fecundity of individuals at each size In this case, there are three prereproductive sizes (maturity at age four). **additional complexities like shrinking or moving more than one class back or forward is easy to incorporate

What to do with a deterministic matrix? Fixed environment assumption is unrealistic. BUT… can evaluate the relative performance of different management/conservation options can use the framework to conduct ‘thought experiments’ not possible in natural contexts can ask whether the results of a short-term experiment/study affecting survival/reproduction could influence population dynamics *can evaluate the relative sensitivity of to different vital rates

What we’ve covered so far: • Translating life histories into stage/size -based matrices • Understanding matrix elements (survival and fecundity rates) • Basic matrix multiplication in fixed environments • Deterministic matrix evaluation ( 1 , stable stage/age) • Initial framework for sensitivity analysis Next: Incorporating demographic & environmental stochasticity

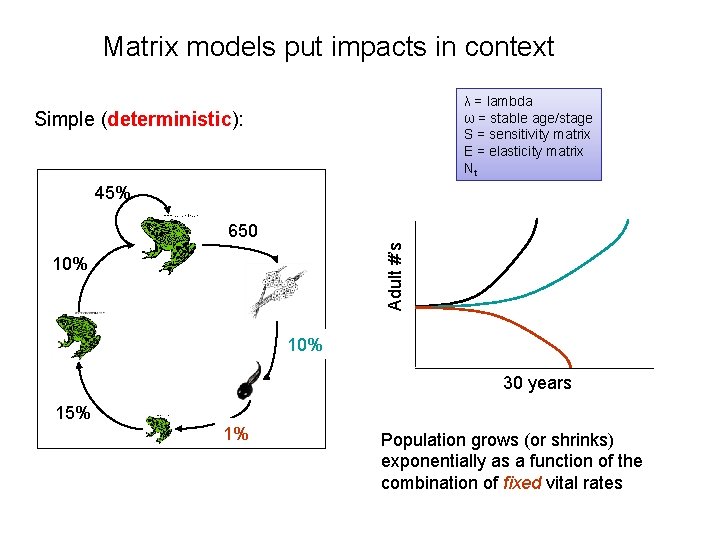
Matrix models put impacts in context λ = lambda ω = stable age/stage S = sensitivity matrix E = elasticity matrix Nt Simple (deterministic): 45% Adult #’s 650 10% 85% 10% 30 years 15% 1% 7% Population grows (or shrinks) exponentially as a function of the combination of fixed vital rates

Matrix models put impacts in context More realistic (stochastic simulation): Drought year Survey yr 1 Se 0. 89 Sl 0. 08 Sj * 0. 15 Sa 0. 08 Sc 0. 47 Fa 498 Adult #’s Long summer 30 years 2 0. 86 0. 07 0. 15 0. 2 0. 6 711 3 0. 66 0. 02 0. 15 0. 09 0. 48 884 9 0. 97 0. 11 0. 15 0. 05 0. 27 509 Population varies from year to year as a function of a randomly drawn matrix

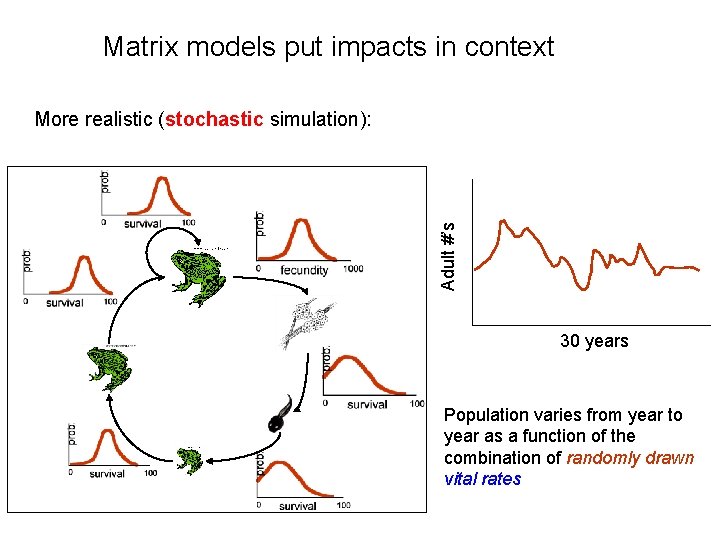
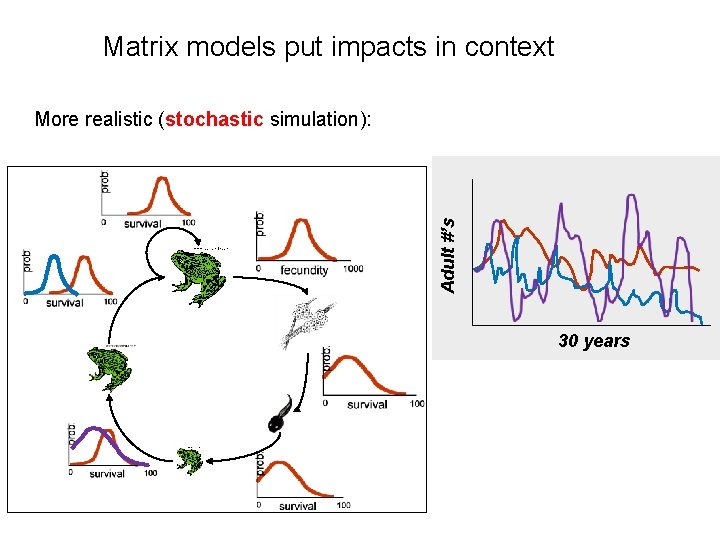
Matrix models put impacts in context Adult #’s More realistic (stochastic simulation): 30 years Population varies from year to year as a function of the combination of randomly drawn vital rates

Matrix models put impacts in context Adult #’s Simulation-based stochastic model: More realistic (stochastic simulation): 30 years

Stochastic projections Issues to consider: 1. Form of stochasticity: in matrix or vital rates? -Environmental stochasticity: Series of fixed matrices (as opposed to mean matrix) -random = env. conditions ‘independent’ (no autocorrelation*) -preserves within year correlations among vital rates (whether you can estimate them or not) Vary individual vital rates each timestep -separate from sampling variation -draw vital rates from distribution describing variation (Lognormal, beta, etc. ) *Either can be mechanistic: vital rates affected by periodic conditions (ENSO, flood recurrence, etc. ) probabilistic draw

Stochastic projections 2. Additional structure -Demographic stochasticity? *Important @ Small population sizes -Monte Carlo sims of individual fate given distributions of vital rates (quasi-extinction is easier…) -Density-dependence in specific vital rates? -vital rate function of density in pop (Nt) or specific stage (Nit) (very difficult to parameterize) -Correlation structure? -within years (common), across years (cross-correlation, harder) -Quasi-extinction threshold? -minimum ‘viable’ level (below which model is unreliable & pop unlikely to recover) -Starting Pop Size?

Stochastic projections Outputs: Can no longer calculate deterministic properties of a single matrix (λ, w, S, E) Stochastic Lambda (λs) -can be calculated from stochastic outputs -estimated by approximation (more on this Thurs…) Extinction Probability (CDF) -how does extinction probability change with time simulated in future? Population Size at t (Nt) -describe variation in est. pop size @ specific points in future Sensitivity/Elasticity -need a new approach (Wed class)

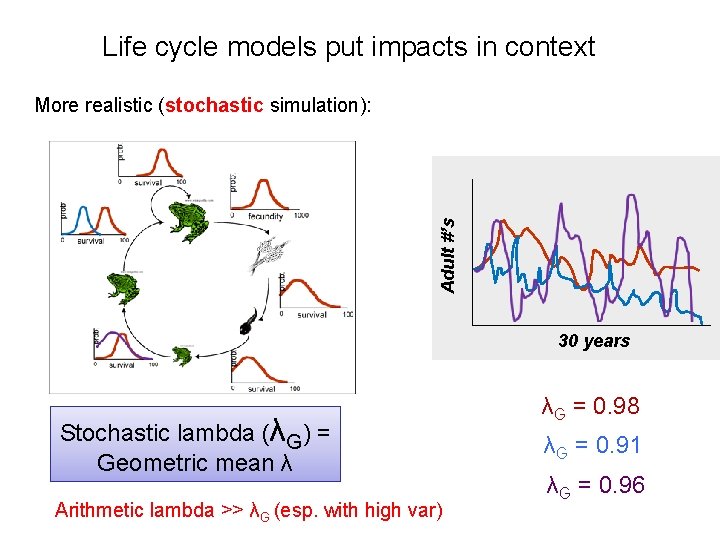
Life cycle models put impacts in context Adult #’s More realistic (stochastic simulation): Simulation-based stochastic model: 30 years Stochastic lambda (λG) = Geometric mean λ Arithmetic lambda >> λG (esp. with high var) λG = 0. 98 λG = 0. 91 λG = 0. 96