Single Input Output Relationships Key Cost Relationships The






- Slides: 19

Single Input. Output Relationships

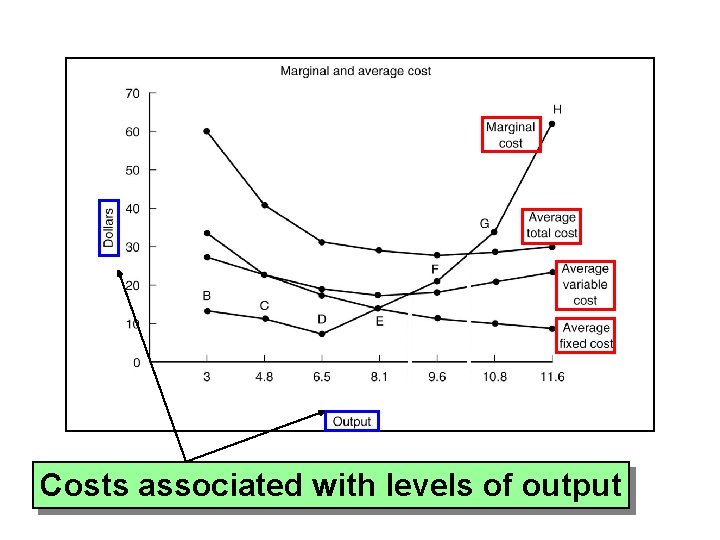
Key Cost Relationships The following cost derivations play a key role in decision-making: Marginal cost = total cost ÷ output

Key Cost Relationships The following cost derivations play a key role in decision-making: Marginal cost = total cost ÷ output Average variable = total variable cost ÷ output cost

Key Cost Relationships The following cost derivations play a key role in decision-making: Marginal cost = total cost ÷ output Average variable = total variable cost ÷ output cost Average total = total cost ÷ output cost

Costs associated with levels of output

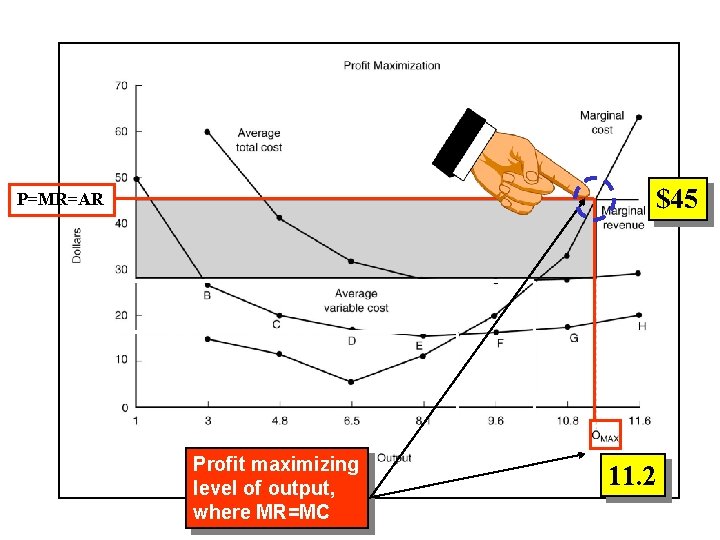
$45 P=MR=AR Profit maximizing level of output, where MR=MC 11. 2

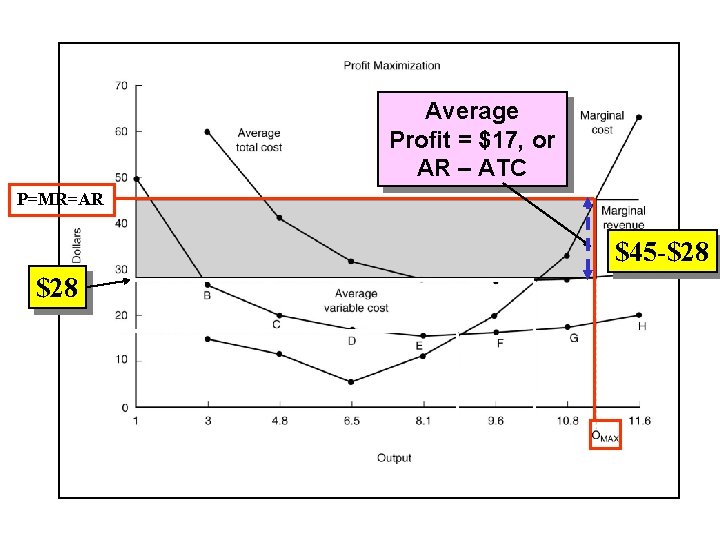
Average Profit = $17, or AR – ATC P=MR=AR $45 -$28

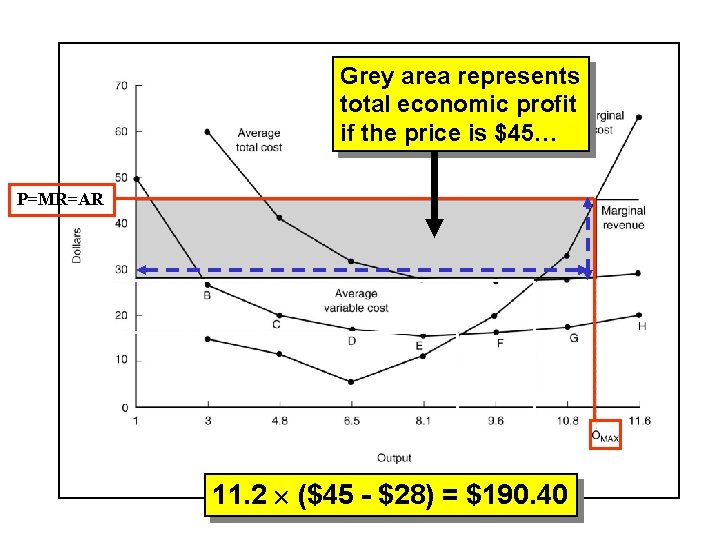
Grey area represents total economic profit if the price is $45… P=MR=AR 11. 2 ($45 - $28) = $190. 40

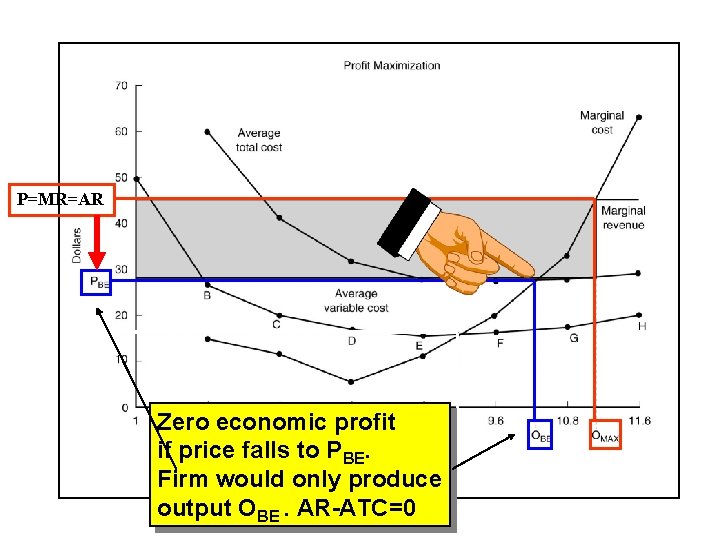
P=MR=AR Zero economic profit if price falls to PBE. Firm would only produce output OBE. AR-ATC=0

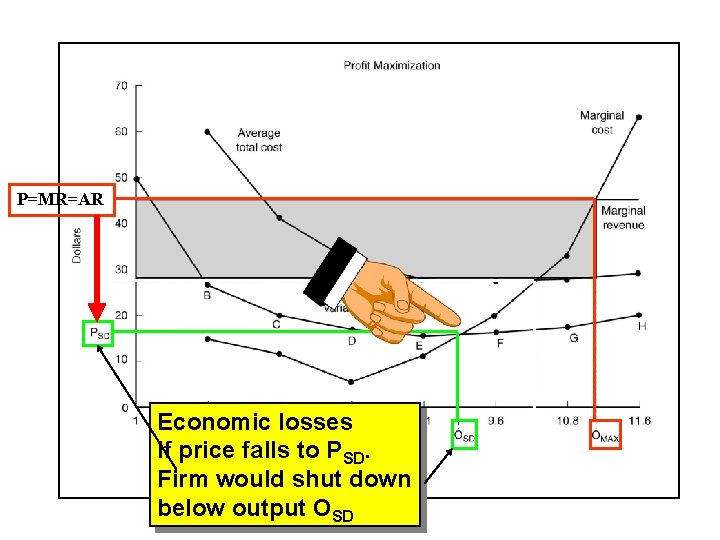
P=MR=AR Economic losses if price falls to PSD. Firm would shut down below output OSD

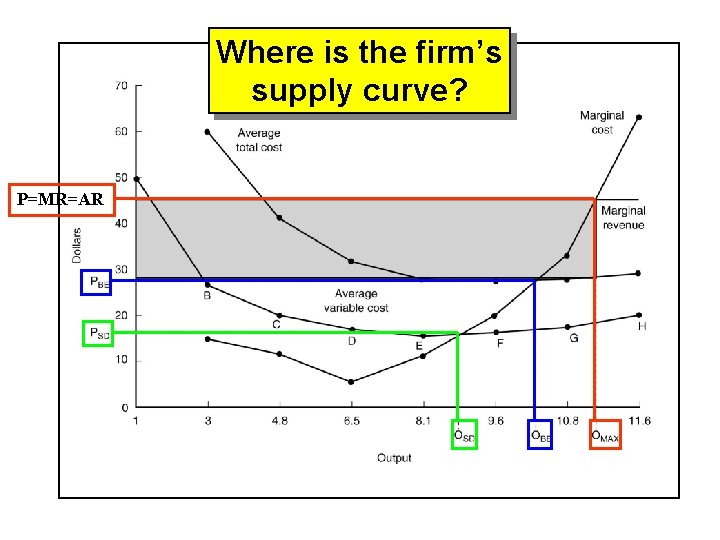
Where is the firm’s supply curve? P=MR=AR

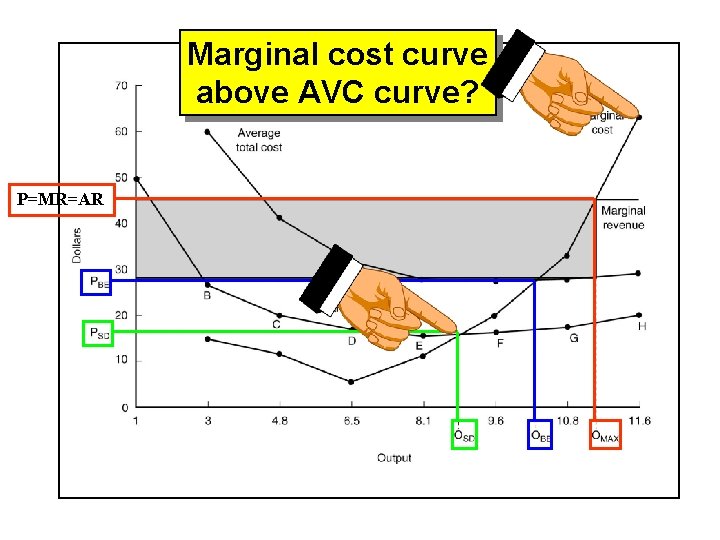
Marginal cost curve above AVC curve? P=MR=AR

Key Input Relationships The following input-related derivations also play a key role in decision-making: Marginal value = marginal physical product × price product

Key Input Relationships The following input-related derivations also play a key role in decision-making: Marginal value = marginal physical product × price product Marginal input = wage rate, rental rate, etc. cost

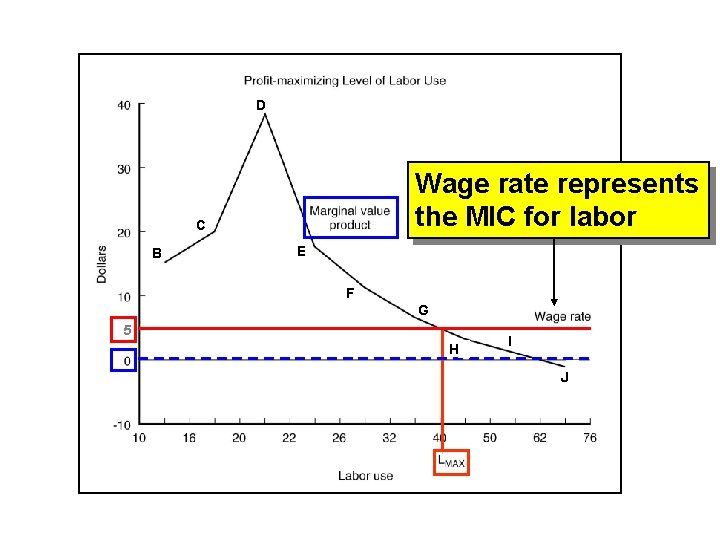
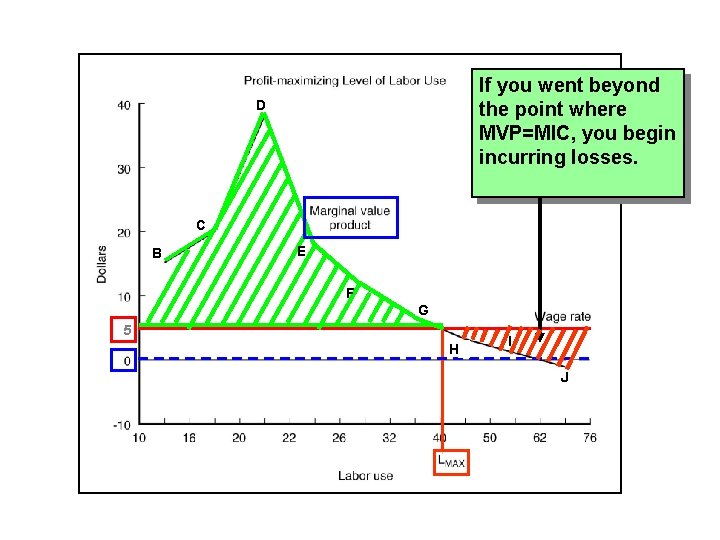
D Wage rate represents the MIC for labor C B E F G 5 H I J

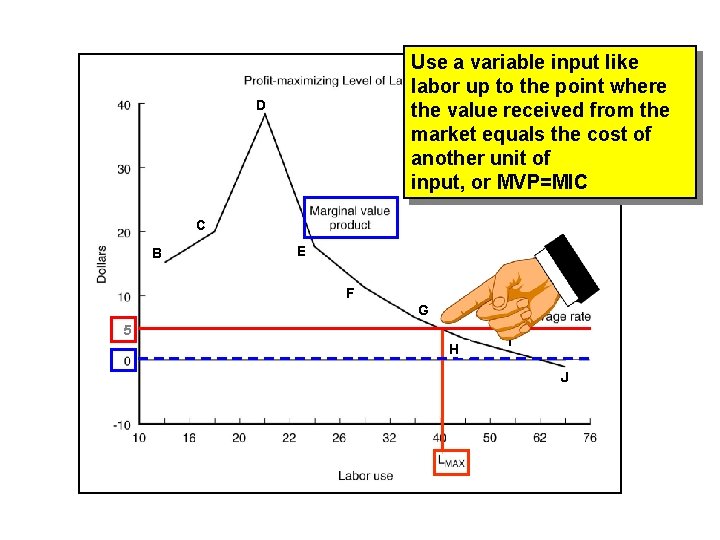
Use a variable input like labor up to the point where the value received from the market equals the cost of another unit of input, or MVP=MIC D C B E F G 5 H I J

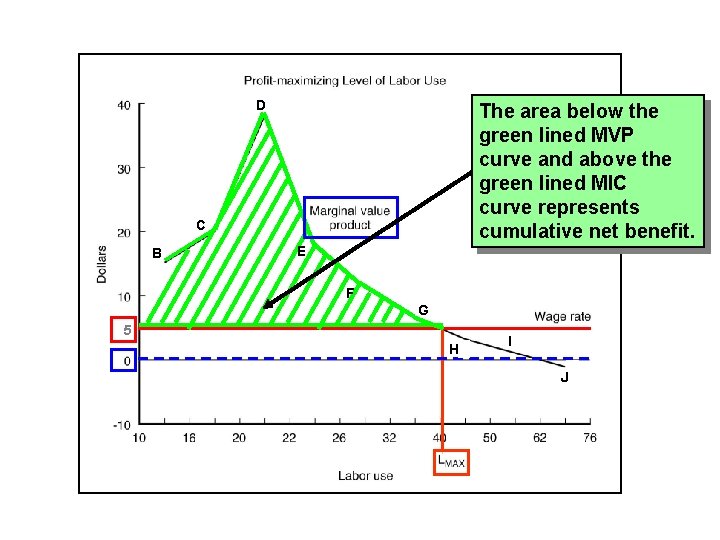
D The area below the green lined MVP curve and above the green lined MIC curve represents cumulative net benefit. C B E F G 5 H I J

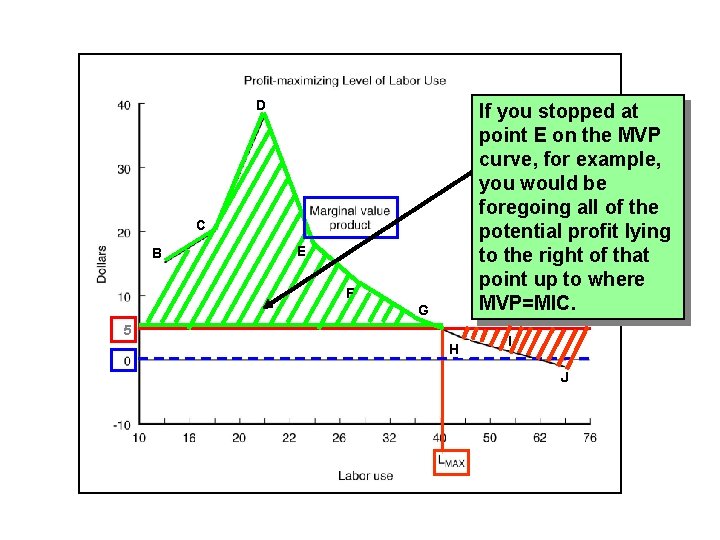
D If you stopped at point E on the MVP curve, for example, you would be foregoing all of the potential profit lying to the right of that point up to where MVP=MIC. C B E F G 5 H I J

If you went beyond the point where MVP=MIC, you begin incurring losses. D C B E F G 5 H I J