SINGLE INDEX MODEL SIM CAPITAL ASSET PRICING MODEL

SINGLE INDEX MODEL (SIM) & CAPITAL ASSET PRICING MODEL (CAPM) MATERI 11

INDIKATOR KOMPETENSI DASAR • Ketepatan menjelaskan konsep dasar Single Index Model (SIM) • Ketepatan menjelaskan konsep dasar Capital Asset Pricing Model (CAPM)

SINGLE INDEX MODEL (SIM) SECTION 1

PENDAHULUAN • Dikembangkan oleh William Sharpe (1963) untuk menyederhanakan perhitungan di model Markowitz. • Dasar penyederhanaannya adalah, bahwa return saham /sekuritas dipengaruhi oleh satu faktor umum yaitu return indeks pasar saham / sekuritasnya sendiri berdasarkan pengamatan orang awam bahwa jika indeks saham suatu negara mengalami peningkatan niscaya saham-saham yang ada di dalamnya cenderung naik juga, dan sebaliknya. • Dalam makul ini, kita hanya akan menggunakan indeks saham saja.

FORMULA & KOMPONEN R i = a i + βi. R M R i = α i + βi. R M + e i ai = α i + ei • Ri = return saham ke-i • ai = variabel random yang menunjukkan komponen dari return saham ke-i yang independen terhadap kinerja pasar • βi = Beta; koefisien yang mengukur perubahan Ri akibat dari perubahan RM • RM = tingkat return dari indeks pasar • αi = nilai ekspektasi dari return sekuritas yang independen terhadap return • ei = kesalahan residu yang merupakan variabel acak; diekspektasikan nilainya adalah nol

FORMULA & KOMPONEN • Dari rumus sebelumnya dapat kita lihat bahwa terdapat dua komponen utama dalam SIM adalah: • Komponen return yang unik; diwakili oleh αi yang tidak punya hubungan / independen terhadap return pasar • Komponen return diwakili oleh βi. RM yang punya hubungan / dependen terhadap return pasar

FORMULA & KOMPONEN • αi hanya mempengaruhi perusahaan tertentu saja (i) dan tidak mempengaruhi perusahaan pada umumnya. Faktor-faktor mikro yang terkait adalah, misalnya, pemogokan karyawan atau kebakaran gudang pabrik. • βi merupakan sensitivitas return suatu saham (i) terhadap return pasar. Beta pasar secara konsensus adalah 1. Misalnya, Beta saham A bernilai 1, 5 maka dikatakan bahwa setiap perubahan return pasar sebesar 1% akan diiikuti dengan perubahan return sajam A sebesar 1, 5% (entah nilainya naik/positif atau turun/negatif)

FORMULA & KOMPONEN (CONTOH) • Return ekspektasi untuk SIM dapat dinyatakan sebagai: E(Ri) = αi + βi. E(RM) • Contoh: Estimasikan besarnya return ekspektasi suatu saham ketika diketahui (1) return ekspektasi dari indeks pasar adalah 20% sedangkan (2) return ekspektasi suatu sekuritas yang independen terhadap pasar adalah 4% dan (3) Beta adalah 0, 75 E(Ri) = 4% + (0, 75) (20%) = 19%

FORMULA & KOMPONEN (CONTOH) • Dari contoh tadi, kita bisa menyatakan bahwa nilai return realisasi berdasarkan model indeks tunggal untuk saham ini adalah Ri = 19% + ei • Makna: Jika ternyata nantinya diketahui bahwa return saham tersebut yang sebenarnya adalah 21% itu berarti bahwa terjadi penyimpangan estimasi sebesar 2% • Penyimpangan estimasi (kesalahan residu) diharapkan untuk semakin mendekati angka 0 estimasi kita, sebagai investor pengguna SIM, semakin baik.

ASUMSI-ASUMSI DALAM SINGLE INDEX MODEL • Asumsi utama: kesalahan residu dari saham ke-i (ei) tidak berkorelasi dengan kesalahan residu dari saham ke-j (ej) • Asumsi kedua: return indeks pasar (RM) dan kesalahan residu untuk tiap-tiap sekuritas (ei) merupakan variabel acak ei tidak berkorelasi dengan RM • Implikasi dari kedua asumsi ini saham-saham bergerak bersama-sama bukan karena efek di luar pasar, melainkan karena mempunyai hubungan yang umum terhadap indeks pasar. • Karena asumsi dibuat untuk menyederhanakan masalah, maka seberapa besar model ini dapat diterima dan mewakili kenyataan sebenarnya akan bergantung dari seberapa besar asumsi-asumsi ini realistis. Jika tidak realistis, maka model ini tidak akurat.

VARIAN RETURN SAHAM – SINGLE INDEX MODEL • Rumus varian return saham berdasarkan SIM adalah: σi 2 = βi 2. σM 2 + σei 2 • Risiko (varian return) saham yang dihitung berdasarkan model ini terdiri dari dua bagian: • Risiko yang berhubungan dengan pasar (βi 2. σM 2) dan • Risiko unik masing-masing perusahaan (σei 2)

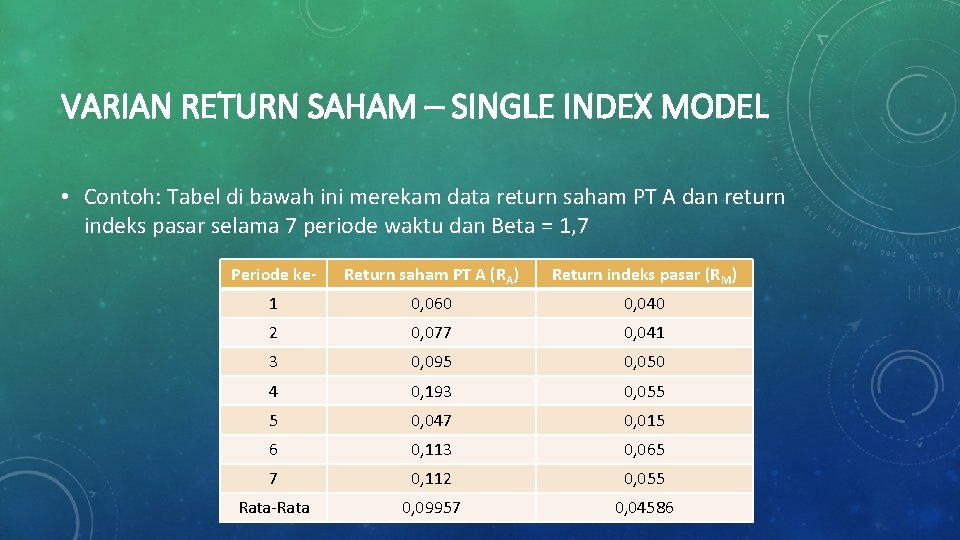
VARIAN RETURN SAHAM – SINGLE INDEX MODEL • Contoh: Tabel di bawah ini merekam data return saham PT A dan return indeks pasar selama 7 periode waktu dan Beta = 1, 7 Periode ke- Return saham PT A (RA) Return indeks pasar (RM) 1 0, 060 0, 040 2 0, 077 0, 041 3 0, 095 0, 050 4 0, 193 0, 055 5 0, 047 0, 015 6 0, 113 0, 065 7 0, 112 0, 055 Rata-Rata 0, 09957 0, 04586

VARIAN RETURN SAHAM – SINGLE INDEX MODEL • E(RA) = αA + βA. E(RM) 0, 09957 = αA + (1, 7)(0, 04586) αA = 0, 0216 • RA = αA + βA. RM + ei menjadi e. A = RA - αA – (βA. RM) • Hitung masing-masing kesalahan residu (e. A) tiap periodenya!

VARIAN RETURN SAHAM – SINGLE INDEX MODEL • Kesalahan residu (e. A) : • Periode 1 = -0, 0296 Periode 5 = 0, 0001 • Periode 2 = -0, 0143 Periode 6 = -0, 0191 • Periode 3 = -0, 0116 Periode 7 = -0, 0031 • Periode 4 = 0, 0779 • Setelah tahu kesalahan residu masing-masing periode, kita bisa mulai mencari total risikonya, yang dilambangkan dengan varian return saham (σA 2)

VARIAN RETURN SAHAM – SINGLE INDEX MODEL • Pertama-tama, ingat bahwa kita punya rumus baku yaitu σA 2 = βA 2. σM 2 + σe. A 2 yang artinya kita harus mencari tahu nilai dari kedua variabel yang ada di rumus tersebut: varian kesalahan residu yang menunjukkan besarnya risiko tidak sistematik di perusahaan A (σe. A 2) dan varian dari return pasar yang menunjukkan risiko indeks pasar yang sistematik (σM 2)

VARIAN RETURN SAHAM – SINGLE INDEX MODEL •

KOVARIAN RETURN SAHAM – SINGLE INDEX MODEL • Bagaimana jika bukan hanya perusahaan A, tapi ada juga perusahaan B di dalam portofolio kita? Maka kita memakai tambahan variabel bernama Kovarian dalam perhitungan total risiko portofolio kita nantinya. • Rumus: σi, j = βi. βj. σM 2

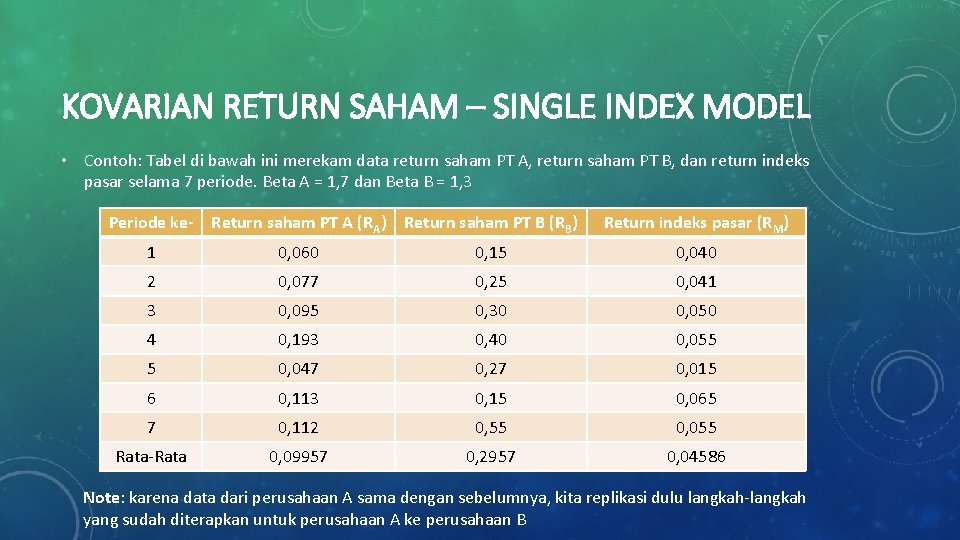
KOVARIAN RETURN SAHAM – SINGLE INDEX MODEL • Contoh: Tabel di bawah ini merekam data return saham PT A, return saham PT B, dan return indeks pasar selama 7 periode. Beta A = 1, 7 dan Beta B = 1, 3 Periode ke- Return saham PT A (RA) Return saham PT B (RB) Return indeks pasar (RM) 1 0, 060 0, 15 0, 040 2 0, 077 0, 25 0, 041 3 0, 095 0, 30 0, 050 4 0, 193 0, 40 0, 055 5 0, 047 0, 27 0, 015 6 0, 113 0, 15 0, 065 7 0, 112 0, 55 0, 055 Rata-Rata 0, 09957 0, 2957 0, 04586 Note: karena data dari perusahaan A sama dengan sebelumnya, kita replikasi dulu langkah-langkah yang sudah diterapkan untuk perusahaan A ke perusahaan B

KOVARIAN RETURN SAHAM – SINGLE INDEX MODEL • E(RB) = αB + βB. E(RM) 0, 2957 = αB + (1, 3)(0, 04586) αB = 0, 236 • RB = αB + βB. RB + ei menjadi e. B = RB - αB – (βB. RM) • Hitung masing-masing kesalahan residu (e. B) tiap periodenya! • Periode 1 = -0, 1381 Periode 5 = 0, 0144 • Periode 2 = -0, 0394 Periode 6 = -0, 1706 • Periode 3 = -0, 0011 Periode 7 = 0, 2424 • Periode 4 = 0, 0924

KOVARIAN RETURN SAHAM – SINGLE INDEX MODEL •

KOVARIAN RETURN SAHAM – SINGLE INDEX MODEL • Ingat! Karena ada dua perusahaan yang terlibat, maka risiko total portofolio tidak bisa dengan naifnya menjumlahkan antara risiko total PT A dengan PT B. Kita menggunakan bantuan Kovarian. σA, B = βA. βB. σM 2 = (1, 7)(1, 3)(0, 00026) = 0, 00057 • Tambahan soal: asumsikan bahwa bobot dana yang dialokasikan ke saham PT A dan PT B masing-masing adalah 50%. Tentukan risiko total dari portofolionya (σP 2)! σP 2 = w. A. σA 2 + w. B. σB 2 + 2. w. A. w. B. σA, B σP 2 = (0, 5)(0, 002) + (0, 5)(0, 00057) + 2(0, 5)(0, 00057) σP 2 = 0, 0035

KOVARIAN RETURN SAHAM – SINGLE INDEX MODEL •

KOVARIAN RETURN SAHAM – SINGLE INDEX MODEL •

CAPITAL ASSET PRICING MODEL (CAPM) SECTION 2

PENDAHULUAN • Ingat bahwa investor memerlukan kemampuan untuk mengestimasi return suatu sekuritas mereka butuh model estimasi CAPM menawarkan solusinya. • Bentuk standar dari CAPM dikembangkan secara terpisah oleh Sharpe (1964), Lintner (1965) dan Mossin (1969). • Namun, Profesor Sharpe lah yang paling dominan dalam pengembangannya, sehingga ia yang meraih penghargaan Nobel di bidang ekonomi

ASUMSI-ASUMSI YANG DIGUNAKAN DI DALAM CAPM 1. Semua investor memiliki cakrawala waktu satu periode yang sama. 2. Semua investor melakukan pengambilan keputusan investasi berdasarkan pertimbangan antara nilai return ekspektasi dan deviasi standar return dari portofolionya 3. Dengan harga sekuritas dan tingkat bunga bebas risiko tertentu dan dengan menggunakan input portofolio yang sama, maka setiap investor akan menghasilkan efficient frontier yang sama pula. 4. Semua investor dapat meminjamkan dan/atau meminjam dana dengan jumlah tak terbatas pada tingkat suku bunga bebas risiko

ASUMSI-ASUMSI YANG DIGUNAKAN DI DALAM CAPM 5. Short sell diijinkan, dan dapat dilakukan sepuasnya. 6. Dengan nilai terkecil pun, investor dapat berinvestasi dan jual-beli sekuritas setiap saat dengan harga yang berlaku. 7. Semua sekuritas dapat dipasarkan secara likuid. 8. Tidak ada biaya transaksi. 9. Tidak ada inflasi. 10. Tidak ada pajak pendapatan pribadi. 11. Investor adalah penerima harga (price-takers). 12. Pasar modal dalam kondisi ekuilibrium.

EKUILIBRIUM PASAR MODAL • Definisi: kondisi pasar pada saat harga-harga sekuritas berada di tingkat yang tidak memberikan insentif lagi untuk melakukan perdagangan spekulatif. • Implikasi: • Semua investor akan memilih portofolio pasar, yaitu semua aktiva yang ada di pasar. • Portofolio pasar ini merupakan portofolio sekuritas berisiko optimal. Yaitu yang berada di efficient frontier menurut Markowitz.

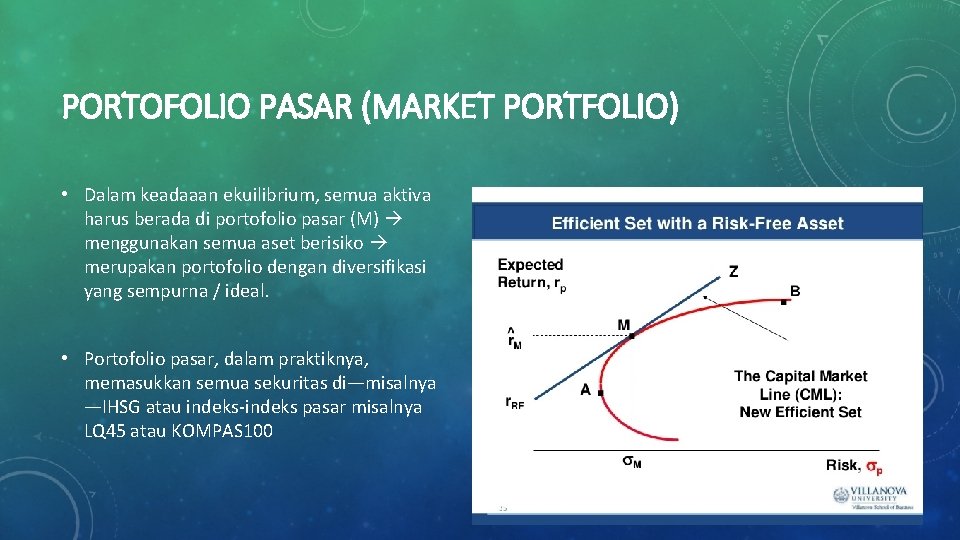
PORTOFOLIO PASAR (MARKET PORTFOLIO) • Dalam keadaaan ekuilibrium, semua aktiva harus berada di portofolio pasar (M) menggunakan semua aset berisiko merupakan portofolio dengan diversifikasi yang sempurna / ideal. • Portofolio pasar, dalam praktiknya, memasukkan semua sekuritas di—misalnya —IHSG atau indeks-indeks pasar misalnya LQ 45 atau KOMPAS 100

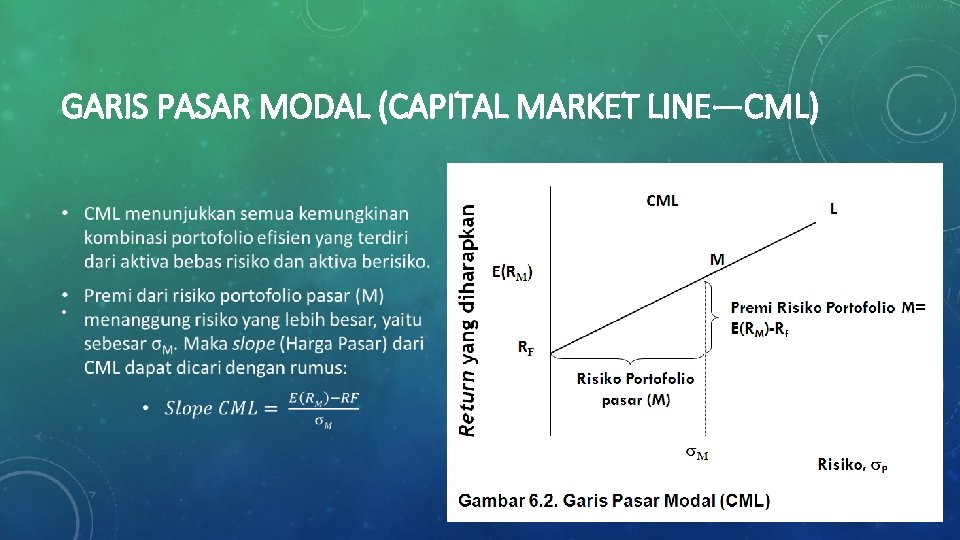
GARIS PASAR MODAL (CAPITAL MARKET LINE—CML) •

GARIS PASAR MODAL (CAPITAL MARKET LINE—CML) •

GARIS PASAR MODAL (CAPITAL MARKET LINE—CML) •

GARIS PASAR MODAL (CAPITAL MARKET LINE—CML) •

GARIS PASAR MODAL (CAPITAL MARKET LINE—CML) • Perhatikan bahwa persamaan rumus di slide sebelumnya, jika kita logika-kan lagi, akan setara dengan persamaan di bawah ini: Return ekspektasi = [Return aset bebas risiko] + [Harga dari Risiko][Besarnya Risiko] • Persamaan di atas adalah awal mula berpikir dari pengembangan bentuk model CAPM yang mengandalkan Garis Pasar Sekuritas (SML)

GARIS PASAR SEKURITAS (SECURITY MARKET LINE—SML) • SML menggambarkan tradeoff antara risiko dan return ekspektasi untuk sekuritas individual, dan merupakan penggambaran secara grafis dari model CAPM. • Risiko yang relevan untuk tiap-tiap sekuritas di dalam portofolio adalah Beta (β), karena dengan portofolio yang optimal kita hanya tinggal mengidentifikasi besarnya risiko sistematik. • Beta portofolio pasar = 1. Bagaimana jika lebih besar / kecil daripada 1 ? ?

GARIS PASAR SEKURITAS (SECURITY MARKET LINE—SML) • Selanjutnya persamaan SML untuk sekuritas ke-I dapat dituliskan sebagai berikut: E(Ri) = RF + βi. [E(RM) – RF] • Persamaan yang sederhana ini (karena hanya bermodalkan dari pemikiran Garis Pasar Modal yang difokuskan menjadi Garis Pasar Sekuritas, namun dapat menghasilkan ekspektasi return yang lebih teliti daripada SIM) membuat Elton dan Gruber (1995) yang menguji konsep milik Sharpe ini menganggap persamaan ini sebagai penemuan terpenting di bidang keuangan.

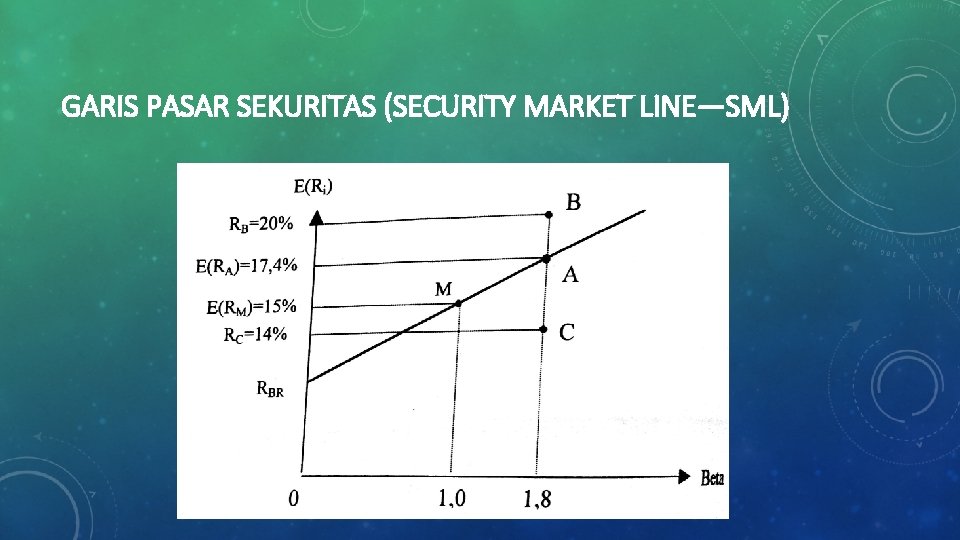
GARIS PASAR SEKURITAS (SECURITY MARKET LINE—SML) • Contoh 1: Return aktiva bebas risiko diketahui adalah sebesar 12%. Return portofolio pasar adalah sebesar 15%. Saham A mempunyai Beta sebesar 1, 8. Return ekspektasi dari saham A ini adalah? E(RA) = 12% + [(15% - 12%) x 1, 8] E(RA) = 12% + 5, 4% E(RA) = 17, 4%

GARIS PASAR SEKURITAS (SECURITY MARKET LINE—SML) • Contoh 2: Saham-saham yang lain, yaitu B dan C mempunyai Beta yang sama dengan saham A. Saham B punya realisasi return sebesar 20% dan saham C mempunyai return realisasi sebesar 14%. • Dari info di atas, Saham B berstatus undervalued (murah) karena dengan risiko yang sama dengan saham A ia mampu memberikan realisasi return yang lebih tinggi. Sedangkan saham C berstatus overvalued (mahal). • Gambarlah SML nya!

GARIS PASAR SEKURITAS (SECURITY MARKET LINE—SML)