Singing the Praises of Octave for Fourier Analysis

Singing the Praises of Octave for Fourier Analysis Martin Connors Athabasca University Canada PICUP Capstone Online Conference August 2021 Oakland Interfaith Gospel Choir: https: //www. oigc. org/about#bio

In Praise of MATLAB®. MATLAB (MATrix LABoratory) is a now usually used as a programming environment incorporating a programming language. Developed in the late 1970 s, it first appeared as a language in a commercial product in 1984. That first version included the Fast Fourier Transform (FFT). • https: //dl. acm. org/doi/pdf/10. 1145/3386331 MATLAB is a successful commercial product used in industry, with a high level of development and support, including many “toolboxes” • https: //www. mathworks. com/products. html? s_tid=gn_ps MATLAB also features much educational support including books such as the individual use downloadable one by founder Cleve Moler: • https: //www. mathworks. com/moler/chapters. html

In Praise of Octave (named after Prof. Octave Levenspiel) is similar to MATLAB but had its roots as a FORTRAN replacement to help students learn. The first version came out in 1994 and now it is Octave 6 • https: //www. gnu. org/software/octave/about Octave is downloadable under the GNU Public Licence (GPL) so is “free”. It is available for Windows, Mac, and many Linux flavors (R Pi? ) • https: //wiki. octave. org/Category: Installation Also can be used online and on tablets https: //octave-online. net/ https: //wiki. octave. org/Octave_for_Android

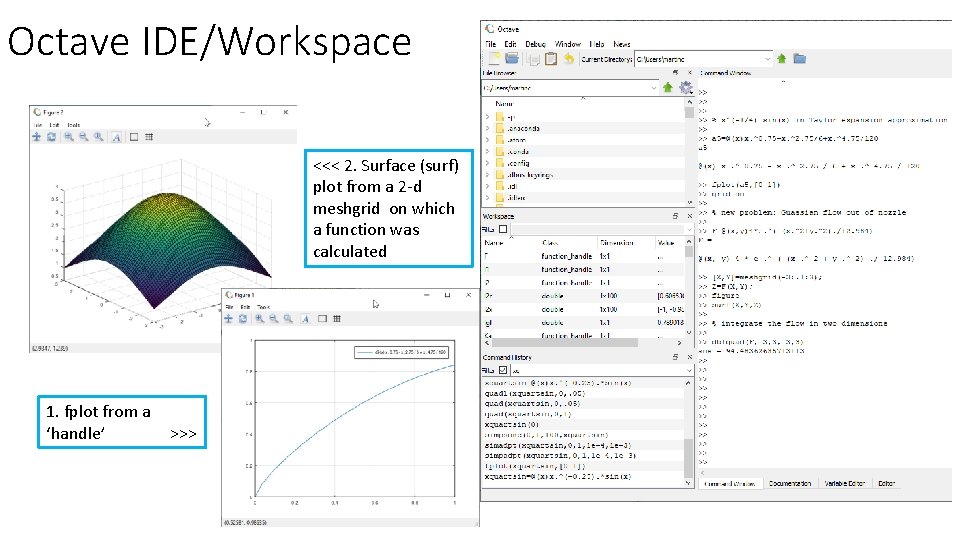
Octave IDE/Workspace <<< 2. Surface (surf) plot from a 2 -d meshgrid on which a function was calculated 1. fplot from a ‘handle’ >>>

Types of Fourier Transforms THE PURPOSE OF COMPUTING IS INSIGHT, NOT NUMBERS - HAMMING “It is remarkable that the sines and cosines are orthogonal over both the continuous interval and sets of discrete, equally spaced points covering the period. This is extremely important because in computing we are usually given only samples of the function at a set of equally spaced points…we can find the coefficients exactly…in the discretely sampled problem…” coefficients determined by integration Continuous coefficients from sums Discrete Fourier Series (periodic, invertable) . Fourier Transform shares many properties but not periodic

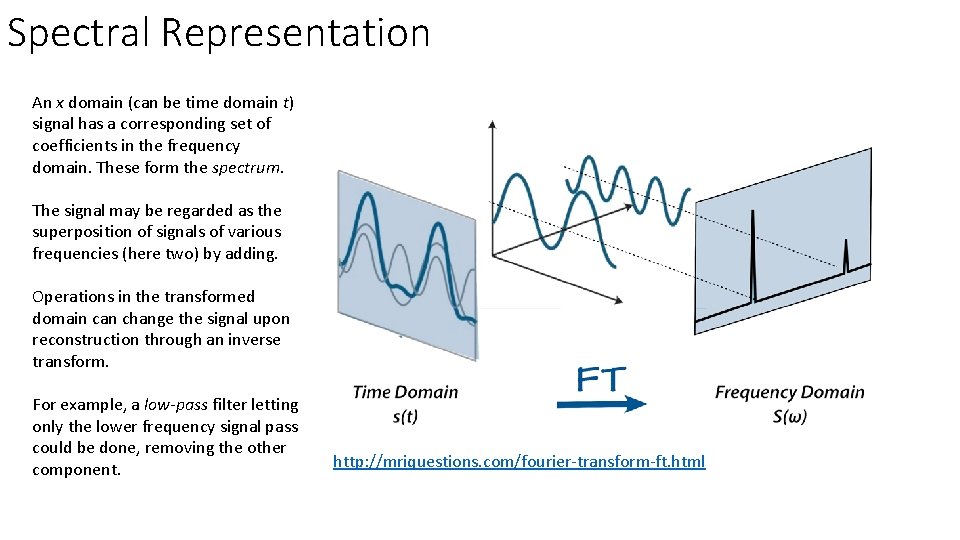
Spectral Representation An x domain (can be time domain t) signal has a corresponding set of coefficients in the frequency domain. These form the spectrum. The signal may be regarded as the superposition of signals of various frequencies (here two) by adding. Operations in the transformed domain can change the signal upon reconstruction through an inverse transform. For example, a low-pass filter letting only the lower frequency signal pass could be done, removing the other component. http: //mriquestions. com/fourier-transform-ft. html

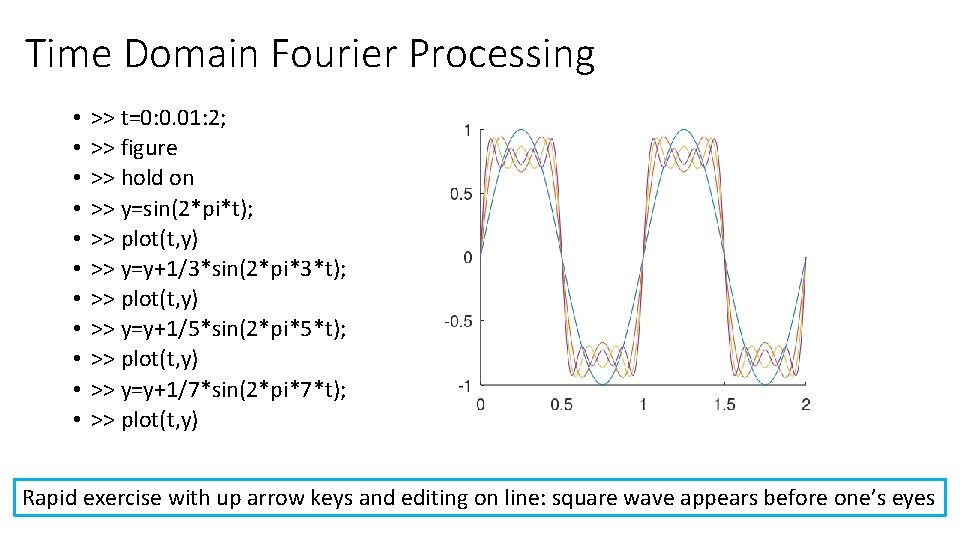
Time Domain Fourier Processing • • • >> t=0: 0. 01: 2; >> figure >> hold on >> y=sin(2*pi*t); >> plot(t, y) >> y=y+1/3*sin(2*pi*3*t); >> plot(t, y) >> y=y+1/5*sin(2*pi*5*t); >> plot(t, y) >> y=y+1/7*sin(2*pi*7*t); >> plot(t, y) Rapid exercise with up arrow keys and editing on line: square wave appears before one’s eyes

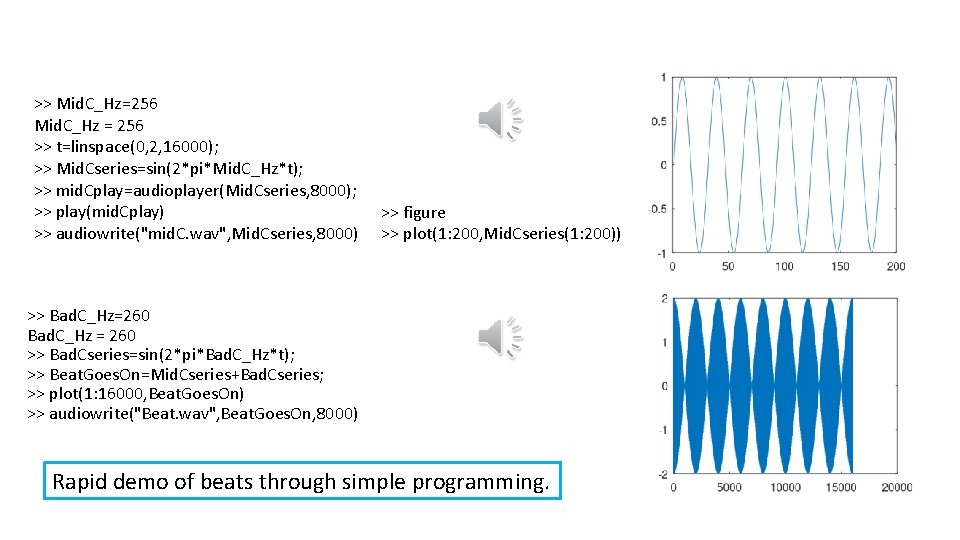
>> Mid. C_Hz=256 Mid. C_Hz = 256 >> t=linspace(0, 2, 16000); >> Mid. Cseries=sin(2*pi*Mid. C_Hz*t); >> mid. Cplay=audioplayer(Mid. Cseries, 8000); >> play(mid. Cplay) >> audiowrite("mid. C. wav", Mid. Cseries, 8000) >> figure >> plot(1: 200, Mid. Cseries(1: 200)) >> Bad. C_Hz=260 Bad. C_Hz = 260 >> Bad. Cseries=sin(2*pi*Bad. C_Hz*t); >> Beat. Goes. On=Mid. Cseries+Bad. Cseries; >> plot(1: 16000, Beat. Goes. On) >> audiowrite("Beat. wav", Beat. Goes. On, 8000) Rapid demo of beats through simple programming.

Personal Data Athabasca University has done BP (Before Pandemic) distance education physics since the late 1990 s, including extensive use of home lab kits. We find that an advantage of home labs is “ownership” of data: students relate more strongly to physics when it comes into their own homes. What could be more personal than one’s own voice?

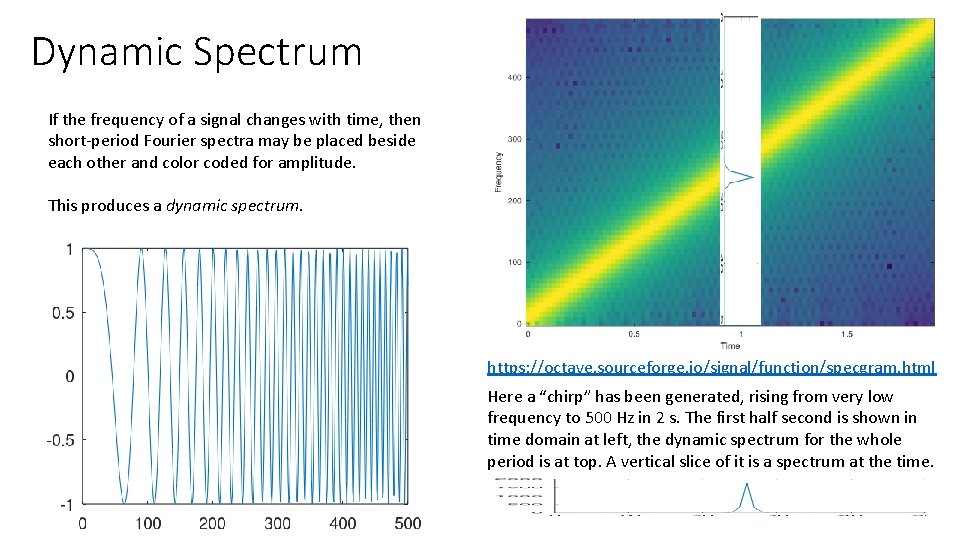
Dynamic Spectrum If the frequency of a signal changes with time, then short-period Fourier spectra may be placed beside each other and color coded for amplitude. This produces a dynamic spectrum. https: //octave. sourceforge. io/signal/function/specgram. html Here a “chirp” has been generated, rising from very low frequency to 500 Hz in 2 s. The first half second is shown in time domain at left, the dynamic spectrum for the whole period is at top. A vertical slice of it is a spectrum at the time.

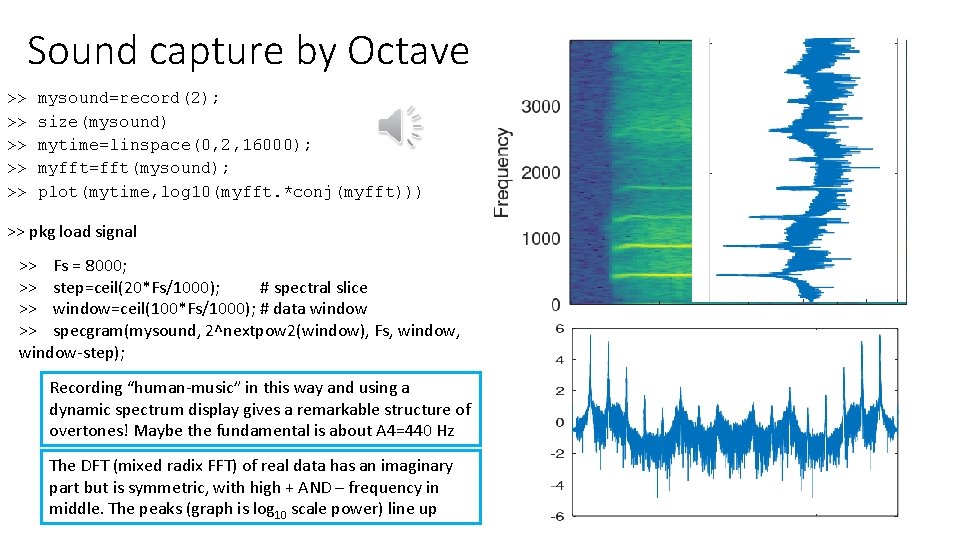
Sound capture by Octave >> >> >> mysound=record(2); size(mysound) mytime=linspace(0, 2, 16000); myfft=fft(mysound); plot(mytime, log 10(myfft. *conj(myfft))) >> pkg load signal >> Fs = 8000; >> step=ceil(20*Fs/1000); # spectral slice >> window=ceil(100*Fs/1000); # data window >> specgram(mysound, 2^nextpow 2(window), Fs, window-step); Recording “human-music” in this way and using a dynamic spectrum display gives a remarkable structure of overtones! Maybe the fundamental is about A 4=440 Hz The DFT (mixed radix FFT) of real data has an imaginary part but is symmetric, with high + AND – frequency in middle. The peaks (graph is log 10 scale power) line up Khöömei is a khün khögjim or “human-music, ” which Uses the human vocal organ as a musical instrument. https: //mongolianstore. com/khoomei-larynx-crooning/

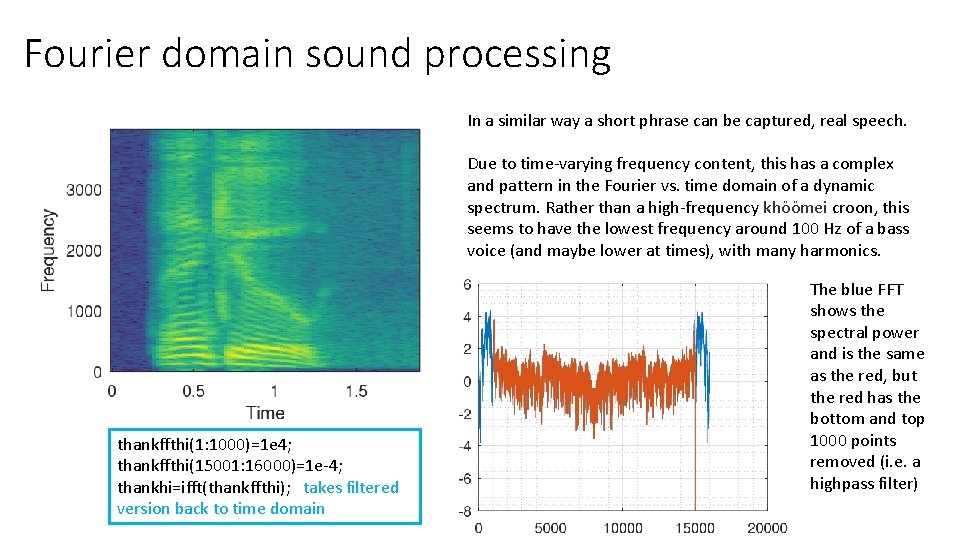
Fourier domain sound processing In a similar way a short phrase can be captured, real speech. Due to time-varying frequency content, this has a complex and pattern in the Fourier vs. time domain of a dynamic spectrum. Rather than a high-frequency khöömei croon, this seems to have the lowest frequency around 100 Hz of a bass voice (and maybe lower at times), with many harmonics. thankffthi(1: 1000)=1 e 4; thankffthi(15001: 16000)=1 e-4; thankhi=ifft(thankffthi); takes filtered version back to time domain The blue FFT shows the spectral power and is the same as the red, but the red has the bottom and top 1000 points removed (i. e. a highpass filter)

In Praise of PICUP With colleague Farook Al-Shamali I participated in the Summer 2018 workshop (Year 2 B. P. ). A great experience. My activities have been mostly in making a math course with lots of examples from physics, using Octave for computation. PICUP has provided lots of ideas and I thank you. In fact I would like to thank you twice…