Sine Graph The Sine Function has this beautiful

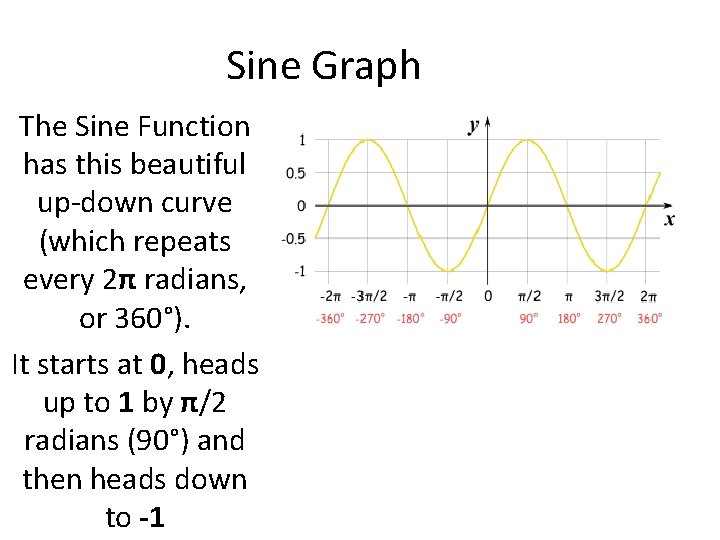
Sine Graph The Sine Function has this beautiful up-down curve (which repeats every 2π radians, or 360°). It starts at 0, heads up to 1 by π/2 radians (90°) and then heads down to -1

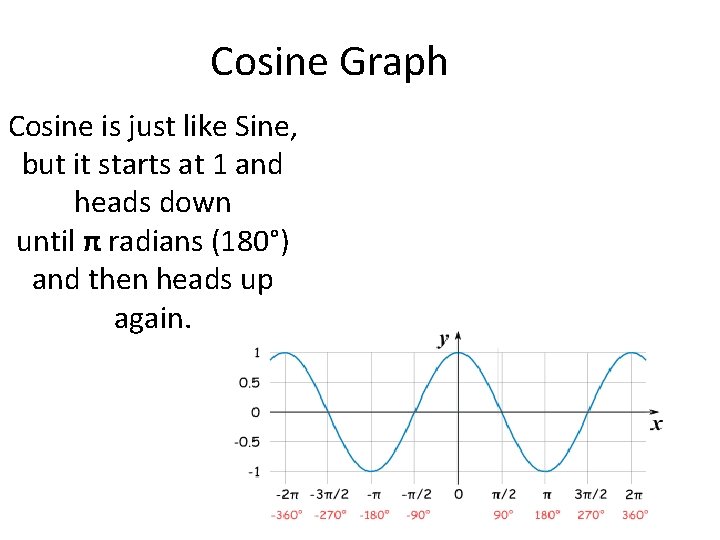
Cosine Graph Cosine is just like Sine, but it starts at 1 and heads down until π radians (180°) and then heads up again.

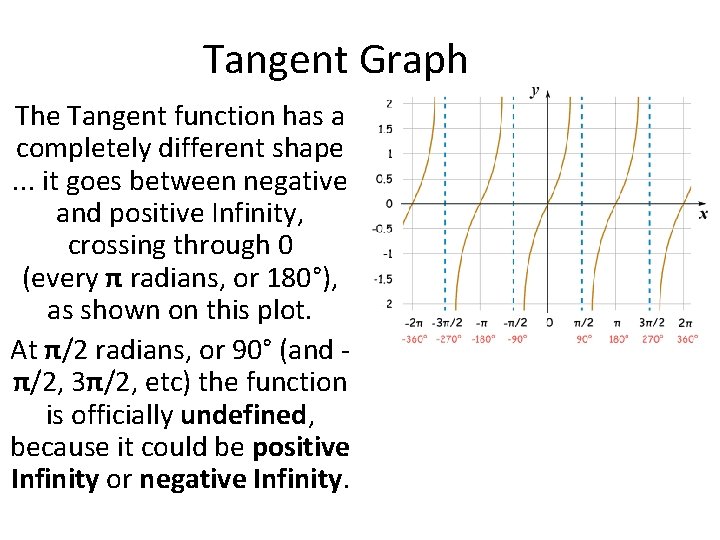
Tangent Graph The Tangent function has a completely different shape. . . it goes between negative and positive Infinity, crossing through 0 (every π radians, or 180°), as shown on this plot. At π/2 radians, or 90° (and π/2, 3π/2, etc) the function is officially undefined, because it could be positive Infinity or negative Infinity.

Inverse Sine, Cosine and Tangent Inverse sine f (x) = sin-1(x) f (x) = arcsin(x) Domain: [-1, 1] Range: (-π/2, π/2) Inverse tangent f (x) = tan-1(x) f (x) = arctan(x) Domain: (-∞, ∞) Range: (-π/2, π/2) Inverse cosine f (x) = cos-1(x) f (x) = arccos(x) Domain: [-1, 1] Range: [0, π/2]

Amplitude, frequency, period and phase shift -A amplitude of the function = (max-min)/2 (vertical stretch of the graph) -B stretch/shrink on the x-axis. (It compresses or expands the graph. ) -B has the following relationship with the period, where P is the period. -C/B the phase shift of the graph (the shift left (if C/B is neg. ) or right (if C/B is pos. )) -D the vertical shift of the graph.

Vertical Shift The graph of y=a+sint can be obtained by shifting the graph of y=sint graph of a vertically a units. If a is positive, the graph is shifted a units upward and if a is negative, the graph is shifted a units downward. The number a is called the vertical shift. Phase shift The graph of y=sin(t-c) can be obtained by shifting the graph of y=sint horizontally c units. If c is positive, the graph is shifted c units right and if c is negative, the graph is shifted c units left. The number is called the phase shift. Amplitude The graph of y=bsint is the same as the graph of y=sint stretched vertically by a factor of b, if b>0. If b<0, then the graph is stretched and reflected across the horizontal axis. The number lbl is called the amplitude of the function. Note that the amplitude is always positive.