Simulation Output Analysis Summary n n n Examples

Simulation Output Analysis

Summary n n n Examples Parameter Estimation Sample Mean and Variance Point and Interval Estimation Terminating and Non-Terminating Simulation Mean Square Errors

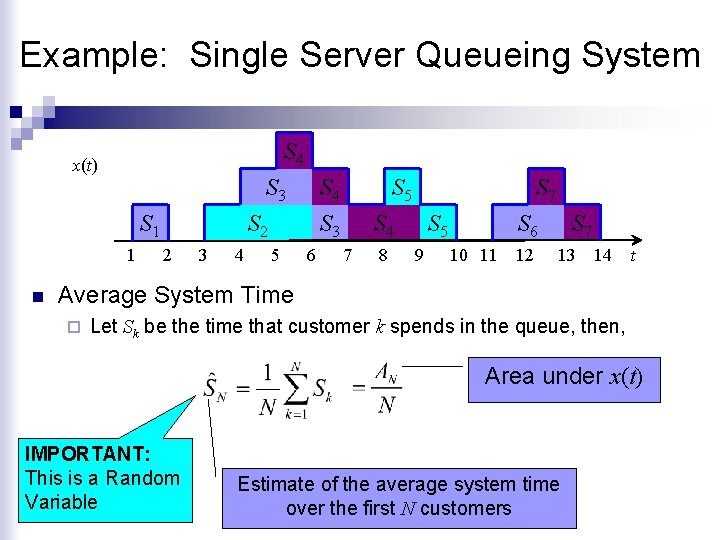
Example: Single Server Queueing System S 4 x(t) S 3 S 1 1 n S 4 S 3 S 2 2 3 4 5 6 S 5 S 7 S 4 7 8 S 5 9 S 7 S 6 10 11 12 13 14 t Average System Time ¨ Let Sk be the time that customer k spends in the queue, then, Area under x(t) IMPORTANT: This is a Random Variable Estimate of the average system time over the first N customers

Example: Single Server Queueing System x(t) T 0 T 1 1 n T 1 2 3 2 T 2 4 3 T 3 5 2 T 2 6 7 T 1 2 T 2 8 9 T 1 10 11 12 T 1 13 14 t Probability that x(t)= i ¨ Let T(i) be the total observed time during which x(t)= i Probability Estimate n T 1 2 T 2 Average queue length Total observation interval n Utilization

Parameter Estimation n n Let X 1, …, Xn be independent identically distributed random variables with mean θ and variance σ2. In general, θ and σ2 are unknown deterministic quantities which we would like to estimate. Random Variable! n Sample Mean: n Τhe sample mean can be used as an estimate of the unknown parameter θ. It has the same mean but less variance than Xi.

Estimator Properties n Unbiasedness: ¨ An estimator is said to be an unbiased estimator of the parameter θ if it satisfies n Bias: ¨ In general, an estimator is said to be an biased since the following holds where bn is the bias of the estimator n If X 1, …, Xn are iid with mean θ, then the sample mean is an unbiased estimator of θ.

Estimator Properties n Asymptotic Unbiasedness: ¨ An estimator is said to be an asymptotically unbiased if it satisfies n Strong Consistency: ¨ An estimator is strongly consistent if with probability 1 n If X 1, …, Xn are iid with mean θ, then the sample mean is also strongly consistent.

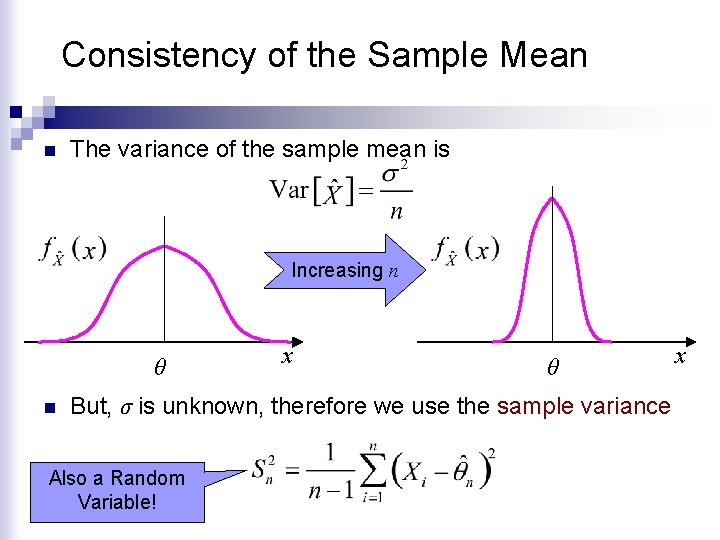
Consistency of the Sample Mean n The variance of the sample mean is Increasing n θ n x θ But, σ is unknown, therefore we use the sample variance Also a Random Variable! x

Recursive Form of Sample Mean and Variance n Let Mj and Sj be the sample mean and variance after the j-th sample is observed. ¨ Also, let M 0=S 0=0. n The recursive form for generating Mj+1 and Sj+1 is n Example: Let Xi be a sequence of iid exponentially distributed random variables with rate λ= 0. 5 (sample. m).

Interval Estimation and Confidence Intervals n n Suppose that the estimator then, the natural question is how confident are we that the true parameter θ is within the interval (θ 1 -ε, θ 1+ε)? Recall the central limit theorem and let a new random variable n n For the sample mean case Then, the cdf of Zn approaches the standard normal distribution N(0, 1) given by

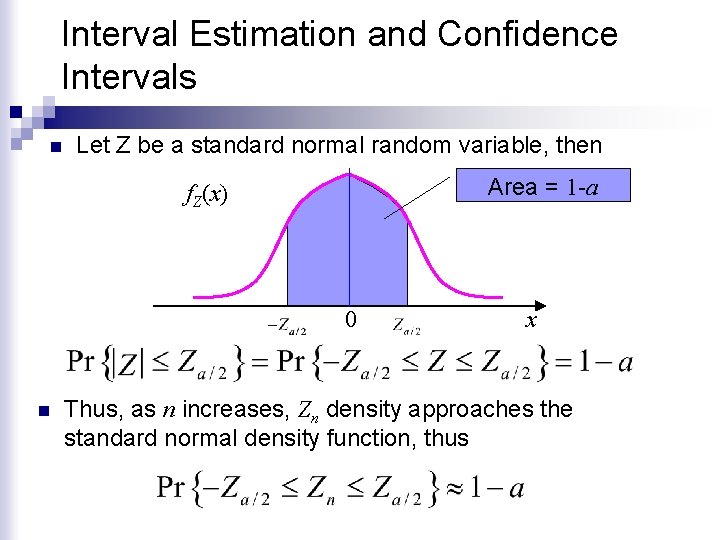
Interval Estimation and Confidence Intervals n Let Z be a standard normal random variable, then Area = 1 -a f. Z(x) 0 n x Thus, as n increases, Zn density approaches the standard normal density function, thus

Interval Estimation and Confidence Intervals n f. Z(x) 0 n Substituting for Zn x Thus, for n large, this defines the interval where θ lies with probability 1 -a and the following quantities are needed The sample mean ¨ The value of Za/2 which can be obtained from tables given a ¨ The variance of which is unknown and so the sample variance is used. ¨

Example n Suppose that X 1, …, Xn are iid exponentially distributed random variables with rate λ=2. Estimate their sample mean as well as the 95% confidence interval. SOLUTION The sample mean is given by From the standard normal tables, a =0. 05, implies za/2 2 Finally, the sample variance is given by n Therefore, for n large, n Sample. Interval. m n n

How Good is the Approximation n The standard normal N(0, 1) approximation is valid as long as n is large enough, but how large is good enough? Alternatively, the confidence interval can be evaluated based on the t-student distribution with n degrees of freedom A t-student random variable is obtained by adding n iid Gaussian random variables (Yi) each with mean μ and variance σ2.

Terminating and Non-Terminating Simulation n Terminating Simulation ¨ There is a specific event that determines when the simulation will terminate n n E. g. , processing M packets or Observing M events, or simulate t time units, . . . ¨ Initial n conditions are important! Non-Terminating Simulation ¨ Interested in long term (steady-state) averages

Terminating Simulation n Let X 1, …, XM are data collected from a terminating simulation, e. g. , the system time in a queue. X 1, …, XM are NOT independent since Xk=max{0, Xk-1 -Yk}+Zk Yk, Zk are the kth interarrival and service times respectively ¨ n Define a performance measure, say n Run N simulations to obtain L 1, …, LN. Assuming independent simulations, then L 1, …, LN are independent random variables, thus we can use the sample mean estimate n

Examples: Terminating Simulation n n Suppose that we are interested in the average time it will take to process the first 100 parts (given some initial condition). Let T 100, j j=1, …, M, denote the time that the 100 th part is finished during the j-th replication, then the mean time required is given by Suppose we are interested in the fraction of customers that get delayed more than 1 minute between 9 and 10 am at a certain ATM machine. Let be the delay of the ith customer during the jth replication and define 1[Dij]=1 if Dij>1, 0 otherwise. Then,

Non-Terminating Simulation n n Any simulation will terminate at some point m < ∞, thus the initial transient (because we start from a specific initial state) may cause some bias in the simulation output. Replication with Deletions The suggestion here is to start the simulation and let it run for a while without collecting any statistics. ¨ The reasoning behind this approach is that the simulation will come closer to its steady state and as a result the collected data will be more representative ¨ warm-up period 0 r Data collection period m time

Non-Terminating Simulation n Batch Means ¨ Group the collected data into n batches with m samples each. ¨ Form the batch average ¨ Take ¨ For the average of all batches each batch, we can also use the warm-up periods as before.

Non-Terminating Simulation n Regenerative Simulation ¨ Regenerative process: It is a process that is characterized by random points in time where the future of the process becomes independent of its past (“regenerates”) 0 n n n Regeneration points time Regeneration points divide the sample path into intervals. Data from the same interval are grouped together We form the average over all such intervals. Example: Busy periods in a single server queue identify regeneration intervals (why? ). In general, it is difficult to find such points!

Empirical Distributions and Bootstrapping n n n Given a set of measurements X 1, …, Xn which are realizations of iid random variables according to some unknown FX(x; θ), where θ is a parameter we would like to estimate. We can approximate FX(x; θ) using the data with a pmf where all measurements have equal probability 1/n. The approximation becomes better as n grows larger.

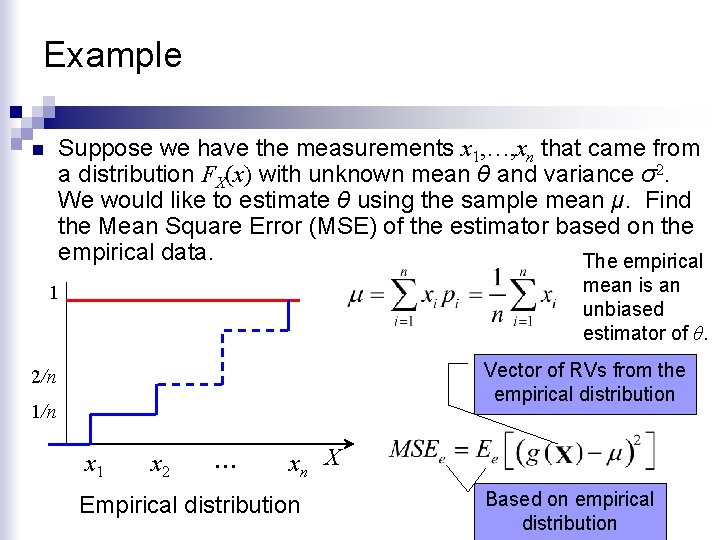
Example Suppose we have the measurements x 1, …, xn that came from a distribution FX(x) with unknown mean θ and variance σ2. We would like to estimate θ using the sample mean μ. Find the Mean Square Error (MSE) of the estimator based on the empirical data. The empirical n mean is an unbiased estimator of θ. 1 Vector of RVs from the empirical distribution 2/n 1/n x 1 x 2 … xn X Empirical distribution Based on empirical distribution

Example Xi is a RV from the empirical distribution Therefore Compare this with the sample variance!