SIMULATION EXAMPLES QUEUEING SYSTEMS Queueing Systems Entities Population

SIMULATION EXAMPLES QUEUEING SYSTEMS

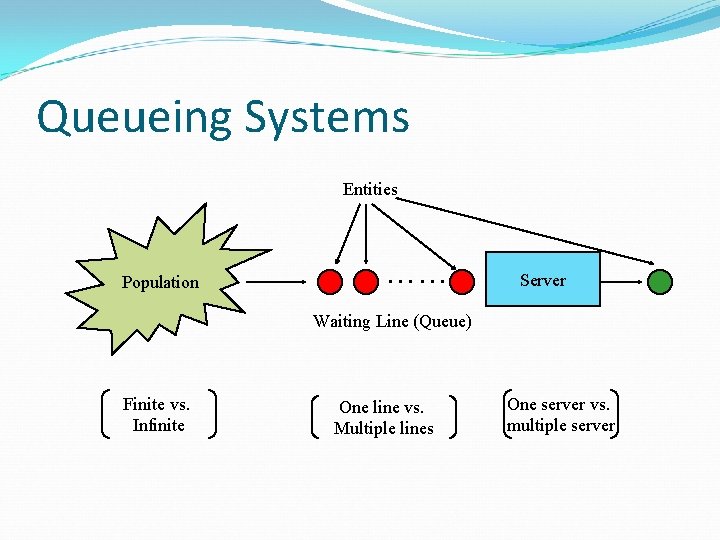
Queueing Systems Entities Population …… Server Waiting Line (Queue) Finite vs. Infinite One line vs. Multiple lines One server vs. multiple server

Characteristics Interarrival and Service Times Exponential (M) Deterministic (D) Erlang (E) General (G) Queue discipline First Come/In First Served/Out (FCFS/FIFO) Last Come/In First Served/Out (LCFS/LIFO) Earliest Due Date (EDD) System Capacity Number of Servers

Applications System Entity Server Hospital Patient Doctor, Nurse Manufacturing Customer order Machine Food Store Purchased grocery Cashier Bank Client Clerk Computer Job CPU or disk Communication Link Data Package Data Channel

Analysis Methods Queueing Theory (Analytical) Simulation Performance Measures Average Waiting Time Maximum Waiting Time Average Number of Entities in the System Maximum Number of Entities in the System Server Utilization Average System Time Maximum System Time

Spreadsheet Example M/U/1 Simulation : Determine waiting time in queue Lindley’s Formula WQi : waiting time in queue for customer i Si : service time for customer i IAi : interarrival time between customers i-1 and i

Hand Simulation of G/G/1 Events: Arrival Event – entry of a unit into the system Departure Event – completion of service on a unit End Event – end of simulation Variables: Q(t) : number of units in queue at time t B(t) : number of units in server at time t L(t) = Q(t) + B(t) : number of units in system at time t

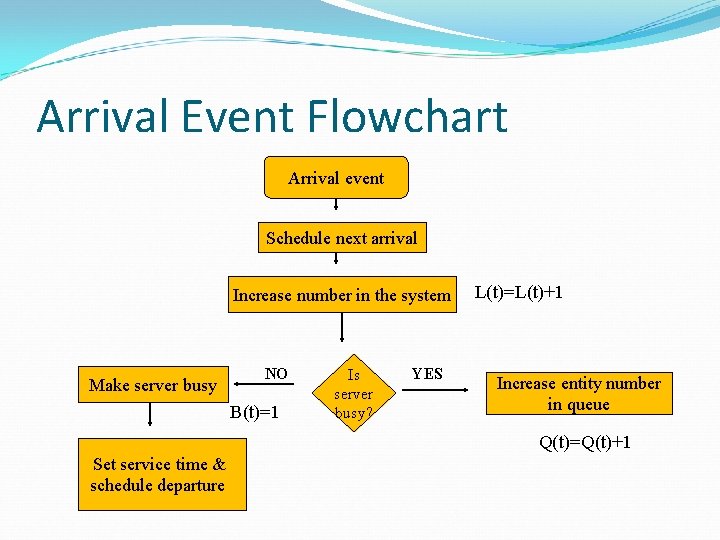
Arrival Event Flowchart Arrival event Schedule next arrival Increase number in the system Make server busy NO B(t)=1 Is server busy? YES L(t)=L(t)+1 Increase entity number in queue Q(t)=Q(t)+1 Set service time & schedule departure

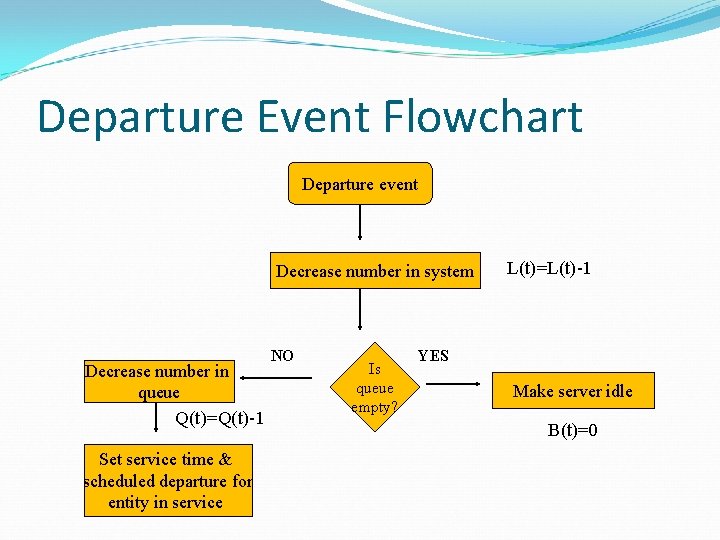
Departure Event Flowchart Departure event Decrease number in system Decrease number in queue Q(t)=Q(t)-1 Set service time & scheduled departure for entity in service NO Is queue empty? L(t)=L(t)-1 YES Make server idle B(t)=0

Simulation by Hand Run simulation for 20 minutes to find • Average Waiting Time • Average Queue Length • Average Utilization Assume the first arrival occurs at zero

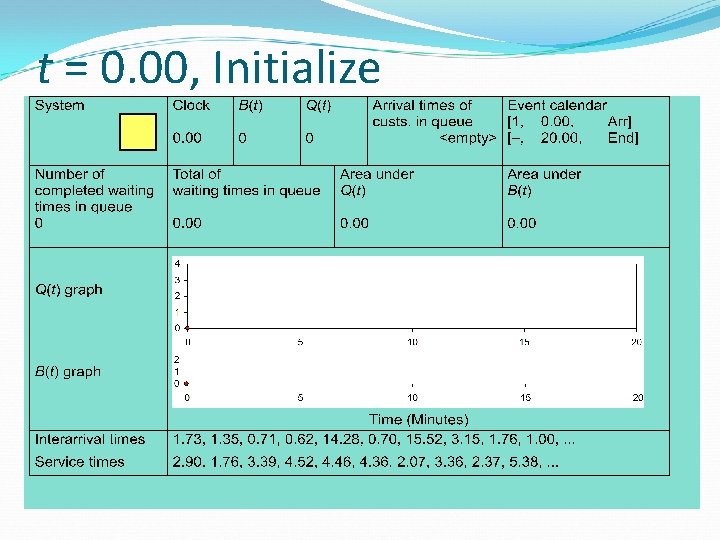
t = 0. 00, Initialize

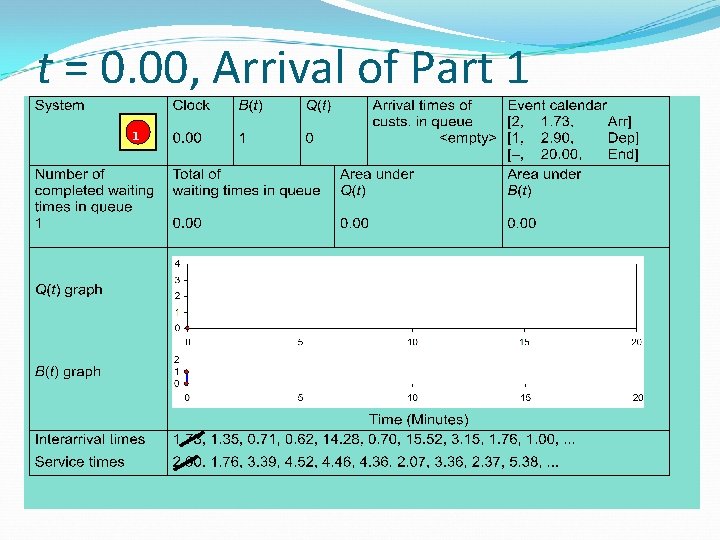
t = 0. 00, Arrival of Part 1 1

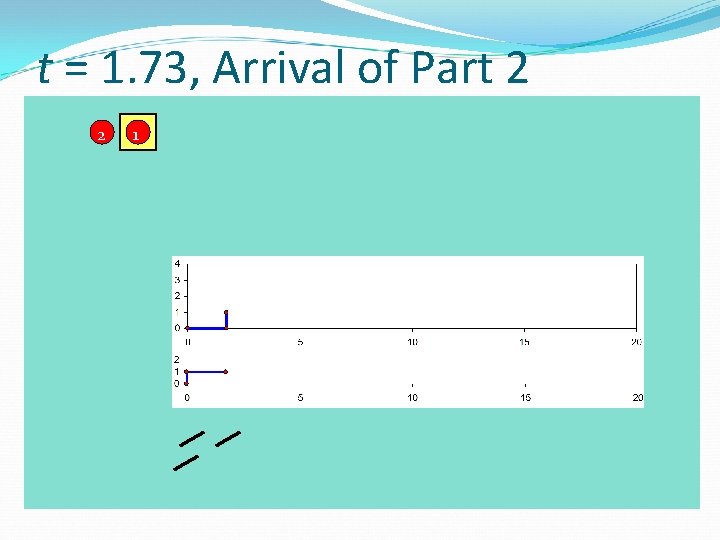
t = 1. 73, Arrival of Part 2 2 1

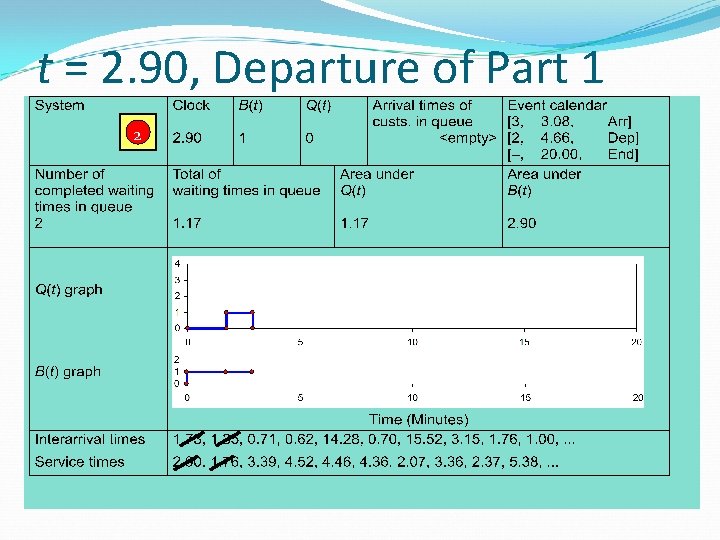
t = 2. 90, Departure of Part 1 2

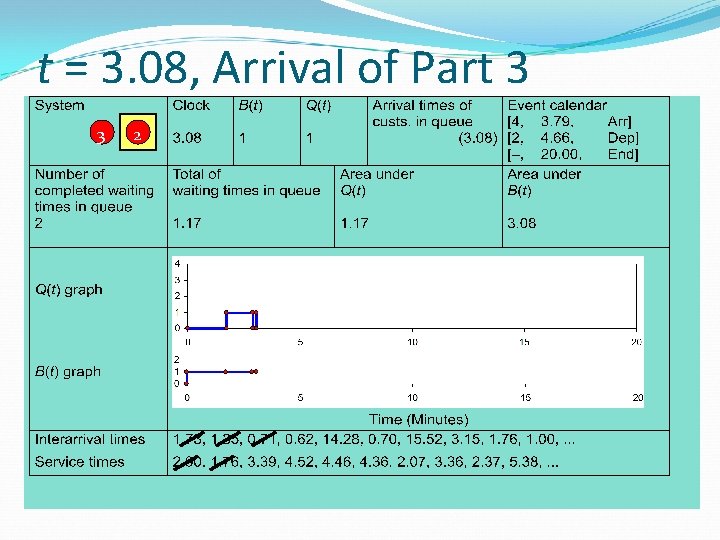
t = 3. 08, Arrival of Part 3 3 2

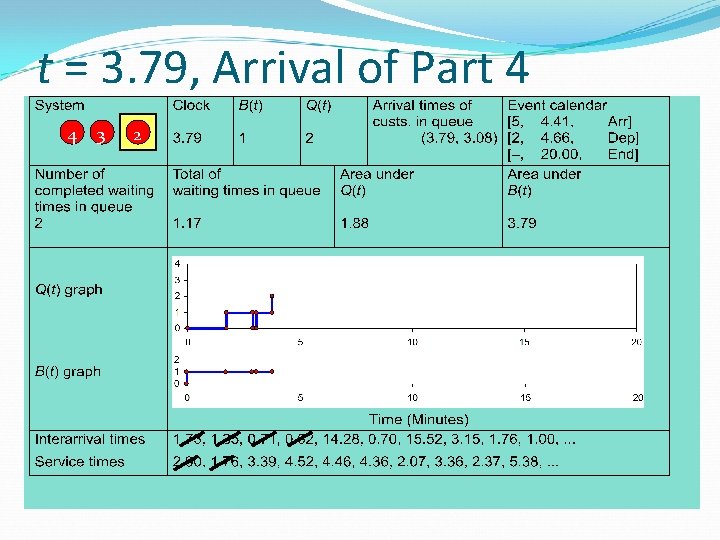
t = 3. 79, Arrival of Part 4 4 3 2

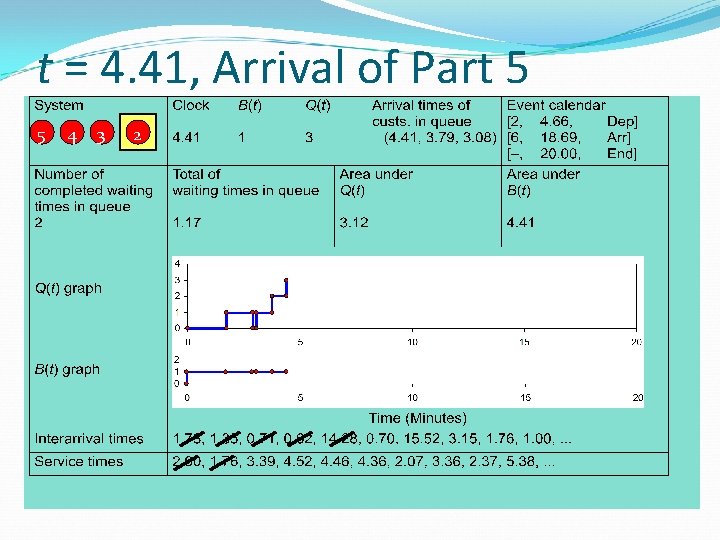
t = 4. 41, Arrival of Part 5 5 4 3 2

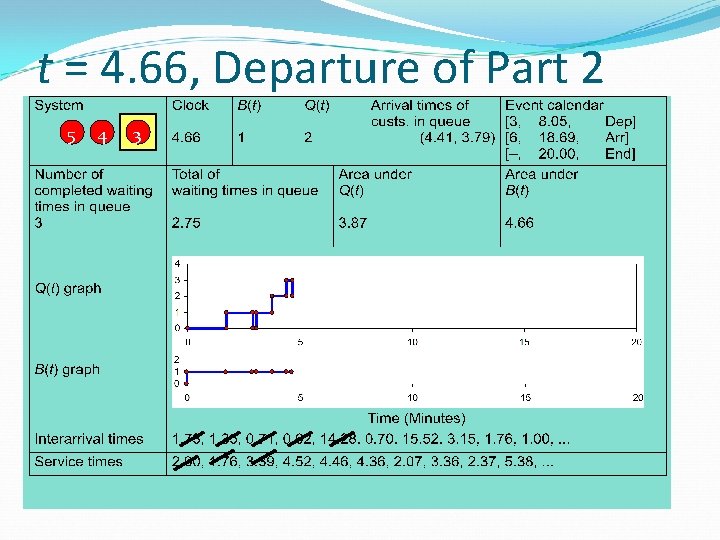
t = 4. 66, Departure of Part 2 5 4 3

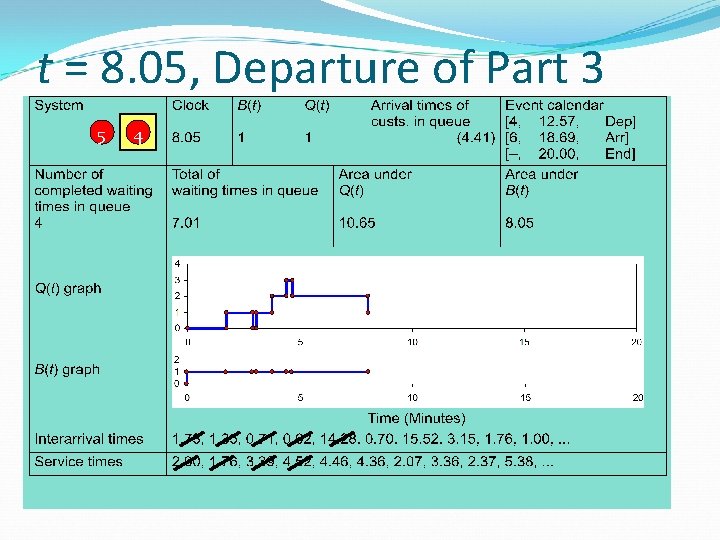
t = 8. 05, Departure of Part 3 5 4

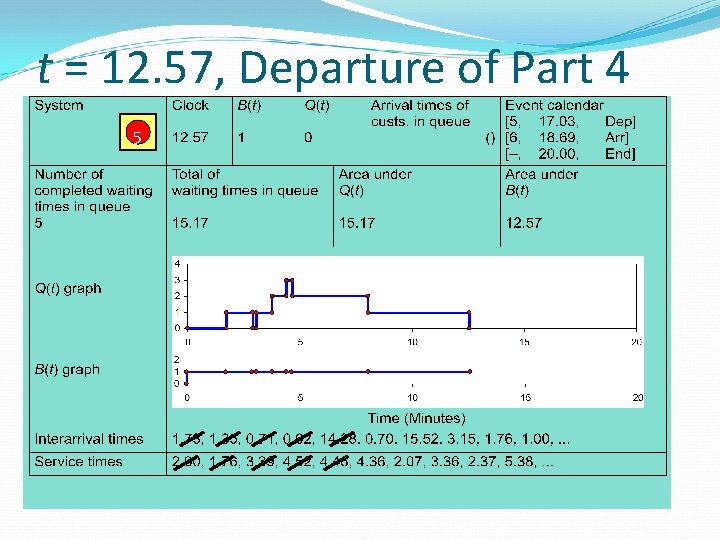
t = 12. 57, Departure of Part 4 5

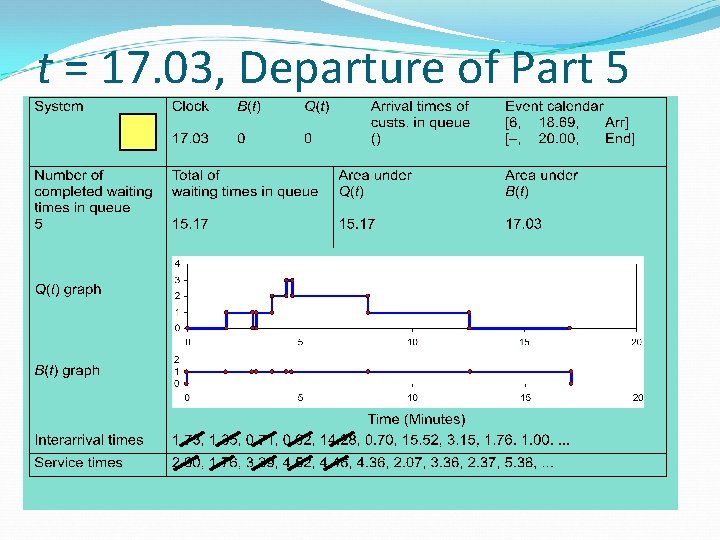
t = 17. 03, Departure of Part 5

t = 18. 69, Arrival of Part 6 6

t = 19. 39, Arrival of Part 7 7 6

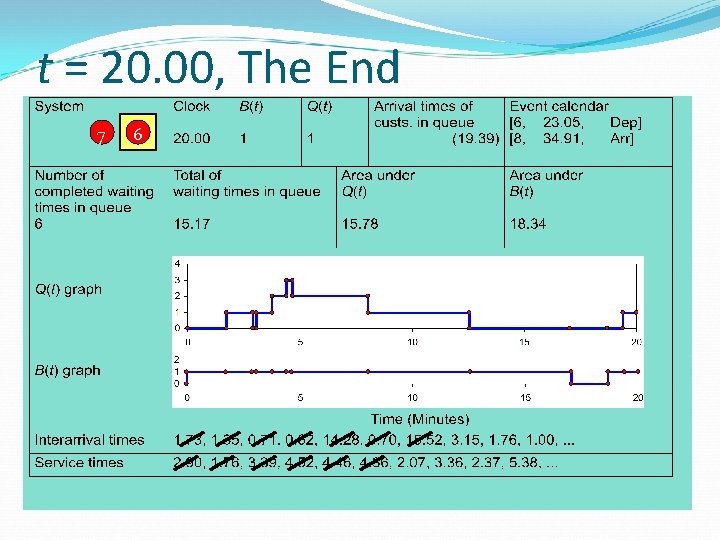
t = 20. 00, The End 7 6

Finishing Up Average waiting time in queue: Time-average number in queue: Utilization of drill press:

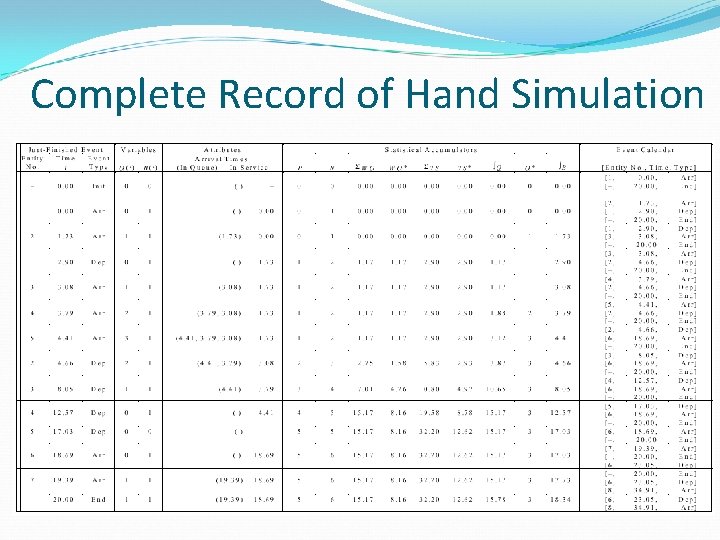
Complete Record of Hand Simulation