SIMULATION BOUNDS FOR EQUIVALENCE VERIFICATION OF ARITHMETIC DATAPATHS

SIMULATION BOUNDS FOR EQUIVALENCE VERIFICATION OF ARITHMETIC DATAPATHS WITH FINITE WORD-LENGTH OPERANDS Namrata Shekhar 1, Priyank Kalla 1, M. Brandon Meredith 2, Florian Enescu 2 1 Department of Electrical and Computer Engineering, University of Utah, Salt Lake City, UT-84112. 2 Department of Mathematics and Statistics, Georgia State University, Atlanta, GA-30303

Outline Problem Overview Application: Arithmetic datapaths in DSP designs Problem modeling Polynomial functions over finite integer rings Limitations of previous work Theory and Applications Results and Conclusions Future work

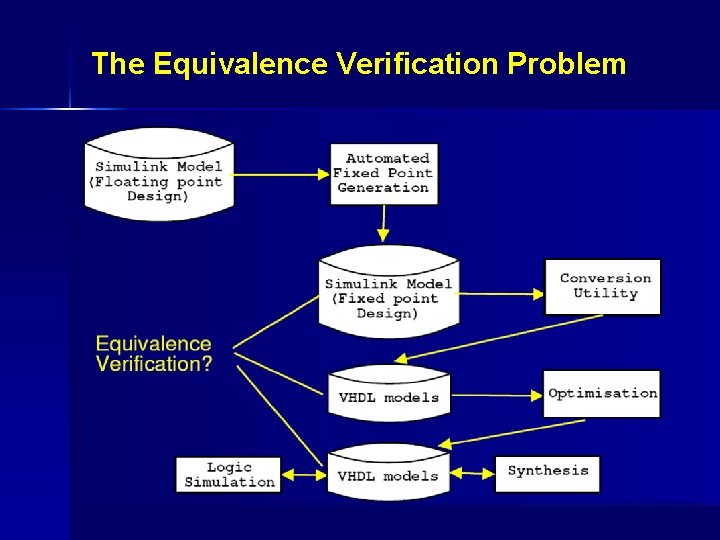
The Equivalence Verification Problem

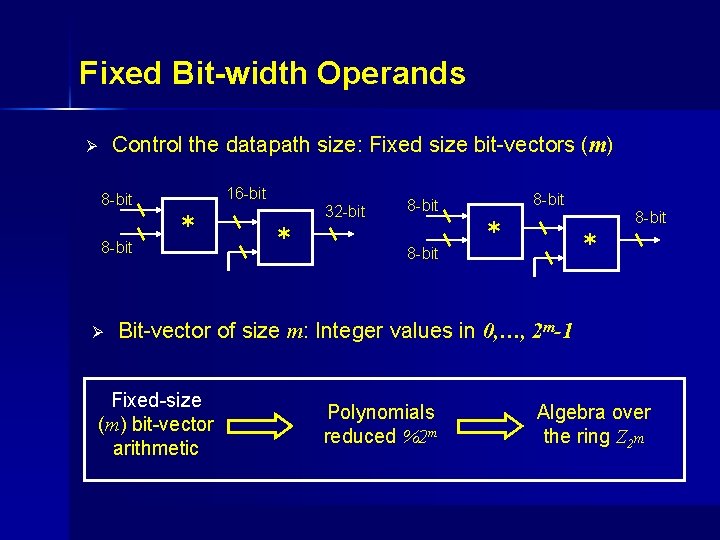
Fixed Bit-width Operands Control the datapath size: Fixed size bit-vectors (m) Ø 16 -bit 8 -bit Ø * 32 -bit * 8 -bit * * Bit-vector of size m: Integer values in 0, …, 2 m-1 Fixed-size (m) bit-vector arithmetic Polynomials reduced %2 m Algebra over the ring Z 2 m

General Datapath Model Bit-vector operands with different word-lengths 20 -bit 8 -bit 12 -bit * 32 -bit * Input variables : {x 1, …, xd} Output variables : f Input bit-widths: {n 1, …, nd} Output width : m. . Model f as polynomial function

Arithmetic Data-path: Implementation Ø Signal Truncation Keep lower-order bits, ignore higher bits. Fractional Arithmetic with rounding Keep higher-order m-bits, round lower order bits. Ø Saturation Arithmetic Saturate at overflow Used in image-processing applications

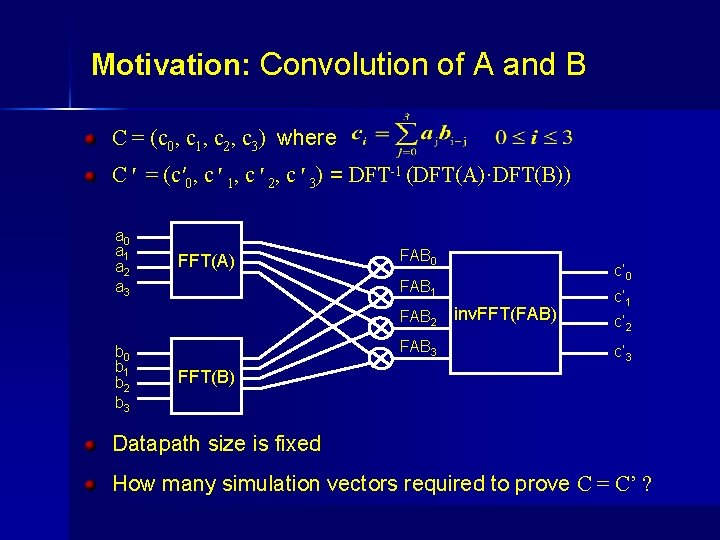
Motivation: Convolution of A and B C = (c 0, c 1, c 2, c 3) where C′ = (c′ 0, c′ 1, c′ 2, c′ 3) = DFT-1 (DFT(A)·DFT(B)) a 0 a 1 a 2 a 3 FFT(A) FAB 0 FAB 2 b 0 b 1 b 2 b 3 c’ 0 FAB 1 FAB 3 inv. FFT(FAB) c’ 1 c’ 2 c’ 3 FFT(B) Datapath size is fixed How many simulation vectors required to prove C = C’ ?

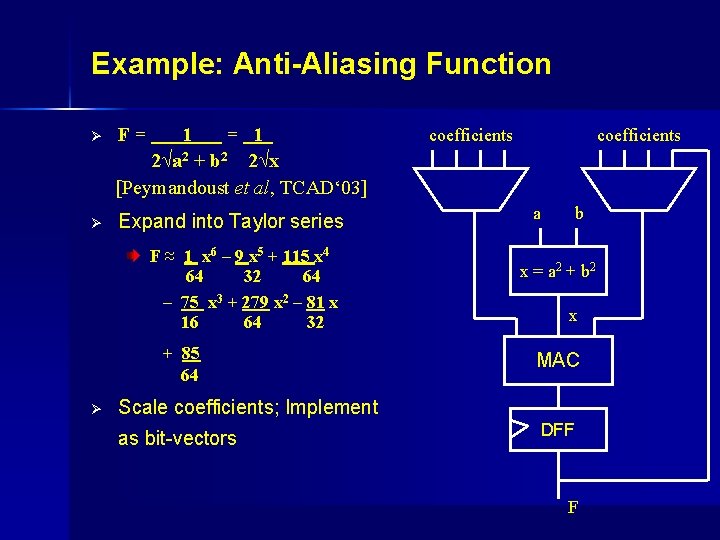
Example: Anti-Aliasing Function Ø F= 1 = 2√a 2 + b 2 2√x [Peymandoust et al, TCAD‘ 03] Ø Expand into Taylor series F ≈ 1 x 6 – 9 x 5 + 115 x 4 64 32 64 – 75 x 3 + 279 x 2 – 81 x 16 64 32 + 85 64 Ø coefficients a b x = a 2 + b 2 x MAC Scale coefficients; Implement as bit-vectors DFF F

Example: Anti-Aliasing Function Ø Implemented as a fixed size datapath in x Ø Ø F 1[15: 0], F 2[15: 0], x[15: 0] F 1 = 156 x 6 + 62724 x 5 + 17968 x 4 + 18661 x 3 + 43593 x 2 + 40244 x + 13281 Ø F 2 = 156 x 6 + 5380 x 5 + 1584 x 4 + 10469 x 3 + 27209 x 2 + 7456 x + 13281 Ø F 1 ≠ F 2 ; F 1[15: 0] = F 2[15: 0] Ø How many vectors required to prove: F 1 % 216 ≡ F 2 % 216

Contributions Abstract the design as a polynomial function Exhaustive simulation is not necessary to prove equivalence Upper bound on the number of vectors To prove equivalence Sufficient to catch errors Bound corresponds to a function in number theory

Previous Work Ø Bit/Word level canonical diagrams Ø BDDs, ZBDDs, BMDs, TEDs Ø SAT and MILP-based techniques Ø Bit-vector decision procedures, Word-level ATPG, SMT Ø Theorem-Proving, term-rewriting Ø Problem model is algebraic

Previous Work: Simulation Ø Ø Reduction in simulation complexity Ø Three-valued logic simulation [Bryant, ACM ’ 91] Ø Utilizing structural information [Brand, ICCAD ’ 92] Ø Automated approach using BDDs [Yuan , ICCAD ‘ 99] Polynomial methods using the fundamental theorem of algebra Ø Generate simulation vectors [Sanchez, HLDVT ‘ 99] Ø Reduce the complexity of model checking [ Raudvere, ICCAD ‘ 05]

Fundamental Theorem of Algebra Ø A degree-k polynomial F(x) has exactly k roots F(x) = x 2 + 6 x = x ( x + 6 ) If F(x) = 0 for k + 1 values, then F(x) is a zero polynomial Can also be extended for multi-variate polynomials Limitations: Results applicable only over unique factorization domains (UFD): Z, Zp, C Ø Z 2 m is a non-UFD

Why is the Problem Difficult? Ø Consider F(x) = x 2 + 6 x in Z 8 F x Ø x+6 x+4 x+2 Degree-2 polynomial has 4 unique roots Ø Ø F F(x) = 0 for 4 vectors, but F(x) ≠ 0 in Z 8 Not applicable to bit-vector arithmetic

Previous Work: Finite Ring Algebra f (x 1, …, xd) % n ≡ g(x 1, …, xd) % n Proving equivalence is NP-hard [Ibarra et al, ACM ‘ 83] Previous approaches f (x 1, x 2, …, xd) – g (x 1, x 2, …, xd) ≡ 0 % 2 m : Zero Equivalence [ICCD ’ 05] Reduction to canonical forms [ICCAD ’ 05] Limitations: Intermediate expression swell No error trace is provided Simulation vector generation: Based on zero equivalence

Zero Equivalence module fixed_bit_width (x, f, g); input [2: 0] x; output [2: 0] f, g; assign f[2: 0] = x 2 + 6 x – 3; assign g[2: 0] = 5 x 2 + 2 x + 5; h(x) = f (x) – g(x) = 4 x 2 + 4 x h(x) ≡ 0 for all values of x in {0, …, 7}: Vanishing polynomial Required: To find if any given expression vanishes Use concepts from ideal membership testing

Ideal Membership Testing Ideal h: % 2 m xi xi % 2 m 0 f Z 2 m[x] g f–g? Z 2 m h: Z 2 m[x] → Z 2 m defined by % 2 m Ideal members map to 0 Test for membership in Ideal of Vanishing Polynomials Representative expression for members of this ideal [Chen, Disc. Math ‘ 96] Use concepts from Number theory and polynomial algebra

Results From Number Theory Find least n such that 2 m|n! Smarandache Function: λ = SF (2 m) λ = SF(23) = 4, since 23|4! Ø n! divides a product of n consecutive numbers 4! divides 99 X 100 X 101 X 102 Ø 2 m divides the product of n consecutive numbers Ø 23 divides the product of 4 consecutive numbers

Results From Number Theory Ø F ≡ G in Z 23 or (F - G) ≡ 0 % 23 23|(F - G) in Z 23 23 divides the product of 4 consecutive numbers If (F-G) is a product of 4 consecutive numbers then 23|(F - G) Ø A polynomial as a product of 4 consecutive numbers? . (x) (x-1) (x-2) (x-3)

Basis for Factorization Ø Y 0(x) = 1 Ø Y 1(x) = (x) Ø Y 2(x) = (x)(x - 1) = Product of 2 consecutive numbers Ø Y 3(x) = (x)(x - 1)(x - 2) = Product of 3 consecutive numbers Ø … Ø Yk(x) = (x – k + 1) Yk-1(x) = Product of k consecutive numbers Rule 1: Factorize into at least Yλ (x) to vanish, where λ = SF(2 m)

Example 1: Vanishing Polynomial Ø 4 th degree polynomial F over Z 23 Ø λ=4 Ø . Degree (x) = k = 4 = λ F can be written as a product of 4 consecutive numbers in x. Ø F is a vanishing polynomial

Constraints on the Coefficient Ø F(x) = 4 x 2 + 4 x = 4 (x)(x-1) % 23 compensated by constant Ø Y 4(x) = (x)(x-1) (x-2)(x-3) missing factor Rule 2: Coefficient has to be a multiple of bk = 2 m/gcd(k!, 2 m) Here, Coefficient of F(x) = 4, Degree of F(x) = 2 b 2 = 23/gcd(2!, 23) = 4 is a multiple of the coefficient Use Rule 1 and Rule 2 to determine if any F(x) = 0 % 2 m

Deciding Vanishing Polynomials Ø Polynomial F in Rule 1 vanishes if Rule 2 Fλ is an arbitrary polynomial over Yλ = Yk is as defined earlier: λ = SF(2 m) ak is an arbitrary integer.

Polynomial Representations Ø Newton’s interpolation formula: Any polynomial F(x) can be written as : Forward difference operator p is the degree of F(x)

Polynomial Representations Newton’s interpolation formula: Any polynomial F(x) can be written as : Forward difference operator p is the degree of F(x)

Reinterpret Vanishing ideal Ø Newton’s interpolation formula: Any polynomial F(x) can be written as : Forward difference operator Yk(x) is as defined earlier p is the degree of F(x)

Reinterpret Vanishing ideal Ø Newton’s interpolation formula: Any polynomial F(x) can be written as : Forward difference operator Yk(x) is as defined earlier p is the degree of F(x)

Polynomial Representations Ø Newton’s interpolation formula: Any polynomial F(x) can be written as is any arbitrary integer Yk(x) is as defined earlier p is the degree of F(x)

Polynomial Representations Ø Any polynomial F(x) in can be written as 0 Rule 1 Fλ is an arbitrary polynomial over Yλ = Yk is as defined earlier: λ = SF(2 m) is an arbitrary integer

Polynomial Representations Ø Any polynomial F(x) in can now be reduced to Fλ is an arbitrary polynomial over Yλ = Yk is as defined earlier: λ = SF(2 m) is an arbitrary integer

Polynomial Representations Ø Ø Any polynomial F(x) in Apply Rule 2 Ø Ø can now be reduced to F(x) vanishes iff ck is a multiple of Check for all ck, where Ø ck evaluated no more than λ times Ø F(x) evaluated no more than λ times

Results By extension, If F(x) ≡ 0 for any λ consecutive values of x in. Further, F(x) – G(x) = 0 → F(x) = G(x) Any λ consecutive values of x are sufficient to prove equivalence

Example Consider f, g over Z 23 λ = SF(23) = 4 f = x 4 + x 2 Simulating, x=0, f=0 g = 2 x 2 Simulating, x=0, g=0 x=1, f=2 x=1, g=2 x=2, f=4 x=2, g=0 x=3, f=2 x=3, g=2 x=4, f=0 x=4, g=0 x=5, f=2 x=5, g=2 x=6, f=4 x=6, g=0 x=7, f=2 x=7, g=2

Extension to Multiple Variables Given d variables x = <x 1, …, xd> with degrees k = < k 1, …, kd> over Z 2 m Basis for d variables: . Rule 1 (for d variables): Factorize into Yλ (x), such that ki ≥ λ for any xi ; λ = SF(2 m)

Example: Vanishing Polynomial Ø 4 th degree polynomial F(x, y) over Z 23 Ø SF(23) = 4 Ø . Degree (x) = k 1 = 4 = SF(23) Degree (y) = k 2 = 1 F can be written as a product of 4 consecutive numbers in x. Ø F is a vanishing polynomial

Effect of Bit-vectors 4 th degree polynomial F(x, y) in Z 21 × Z 22 → Z 23 λ=4. Define Rule 1(extended): Factorize into Yk(x), such that ki ≥ μi for any xi. F = Y 2(x) · Y 1(y) ≡ 0 % 23

Results By extension, for F(x) over If F(x) ≡ 0 for any μi consecutive values of xi in. Total number of vectors: Further, F(x) – G(x) = 0 → F(x) = G(x) over To prove equivalence, we need vectors

Example Consider f, g over Z 22 × Z 2 → Z 23 λ = 4, μ 1 = 4 ; μ 2 = 2 Required: μ 1. μ 2 = 8 vectors f = x 4 y+ x 2 y g = 2 x 2 y Simulating, x=0, y=0, f=0 x=0, y=0, g=0 x=1, y=0, f=0 x=1, y=0, g=0 x=2, y=0, f=0 x=2, y=0, g=0 x=3, y=0, f=0 x=3, y=0, g=0 x=0, y=1, f=0 x=0, y=1, g=0 x=1, y=1, f=2 x=1, y=1, g=2 x=2, y=1, f=4 x=2, y=1, g=0 x=3, y=1, f=2 x=3, y=1, g=2

Experimental Setup Ø Distinct RTL designs are input to GAUT [U. de LESTER, 2004] Ø Extract data-flow graphs for RTL designs Ø Construct the corresponding polynomial representations (F, G) Extract bit-vector sizes for inputs and outputs Ø Determine the maximum number of simulation vectors required Ø Check for equivalence or determine bugs

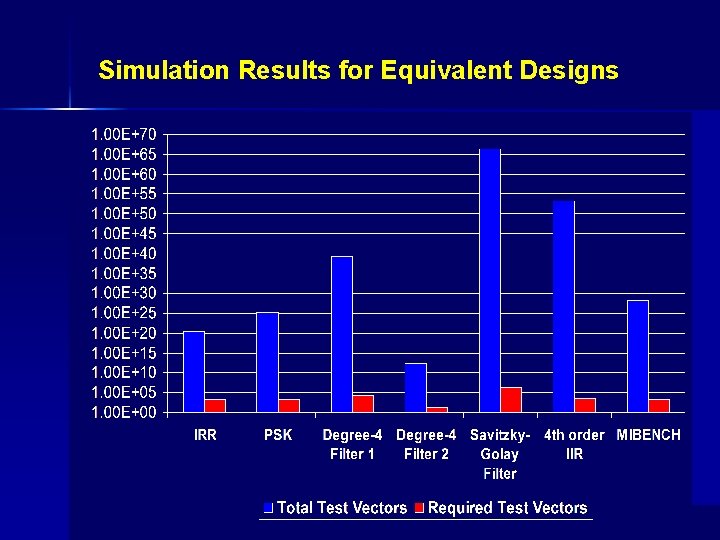
Simulation Results for Equivalent Designs

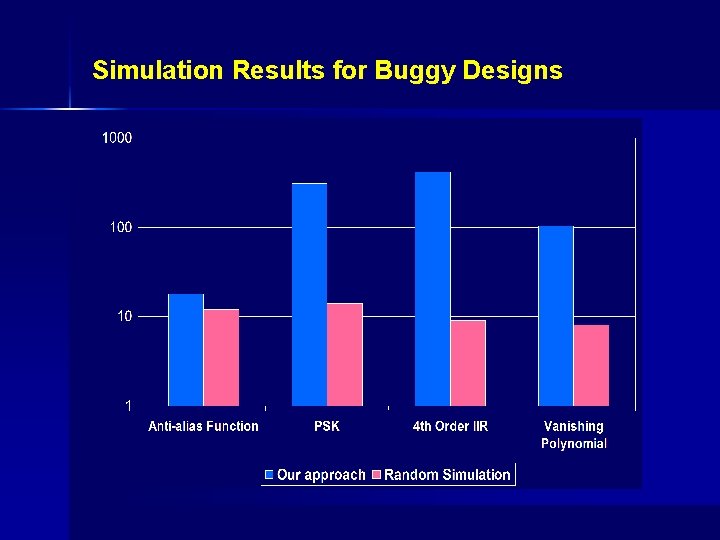
Simulation Results for Buggy Designs

Limitations a[7: 0] b[7: 0] c[7: 0] a[7: 0] b[7: 0] + c[7: 0] + ≠ t 1[7: 0] a = 127 b=1 c = 255 t 2[7: 0] + + f 1[8: 0] f 2[8: 0] f 1 = 383 a = 127 b=1 c = 255 f 2 = 127

Conclusions Ø Technique to verify equivalence of polynomial RTL computations Ø Bit-vector arithmetic is polynomial algebra over the system of finite integer rings Ø Exhaustive simulation is not necessary to prove Ø Results based on concepts from number theory and polynomial algebra

Questions ?

Polynomial Abstraction If (x > 2 b’ 10) then y = x * x Else y = x*x Traditional modeling. Proposed modeling: y as a polyfunction from : Unique representation Issues with the proposed abstraction: Scalability