Simulation and Analysis of Entrance to Dahlgren Naval

Simulation and Analysis of Entrance to Dahlgren Naval Base Jennifer Burke MSIM 752 Final Project December 7, 2007

Background n n n Model the workforce entering the base Force Protection Status Security Needs Possibility of Re-Opening Alternate Gate 6 am – 9 am ~5000 employees n n n 80% Virginia 20% Maryland Arena 10. 0

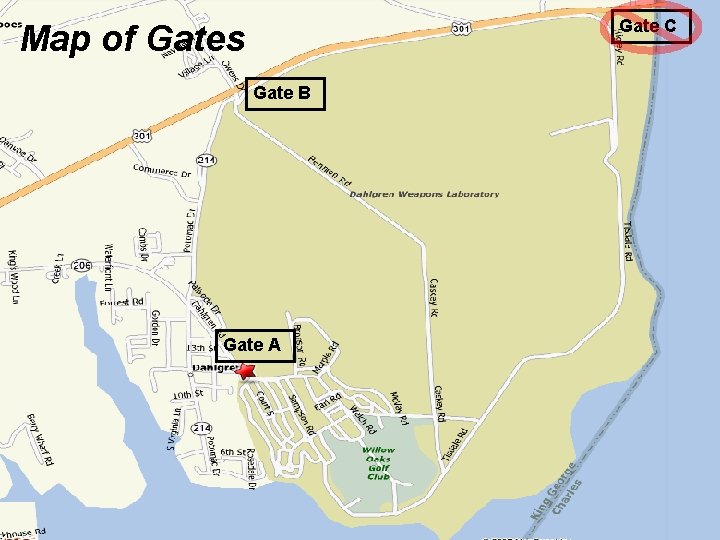
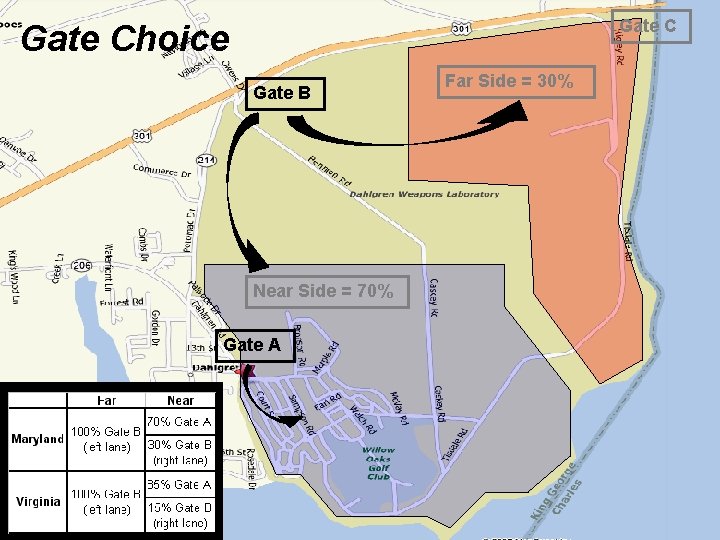
Gate C Map of Gates Gate B Gate A

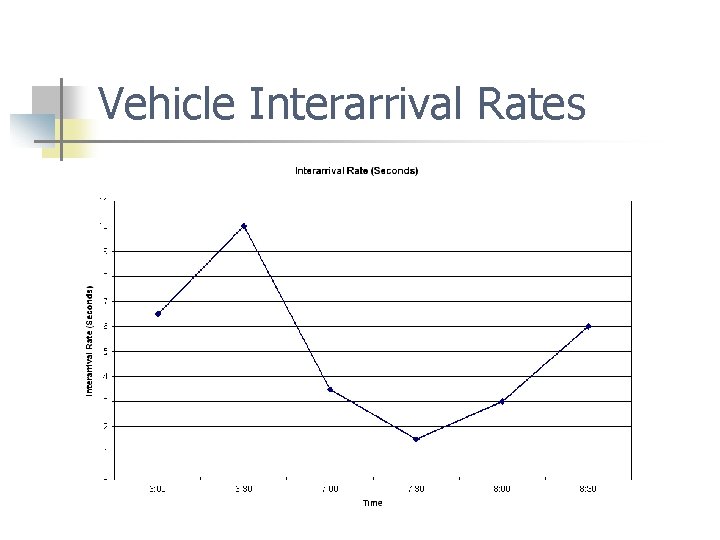
Probability Distributions n Employee arrival process n n Rates vary over time How many people in each vehicle? Which side of base do they work on? Which gate will they enter?

Vehicle Interarrival Rates

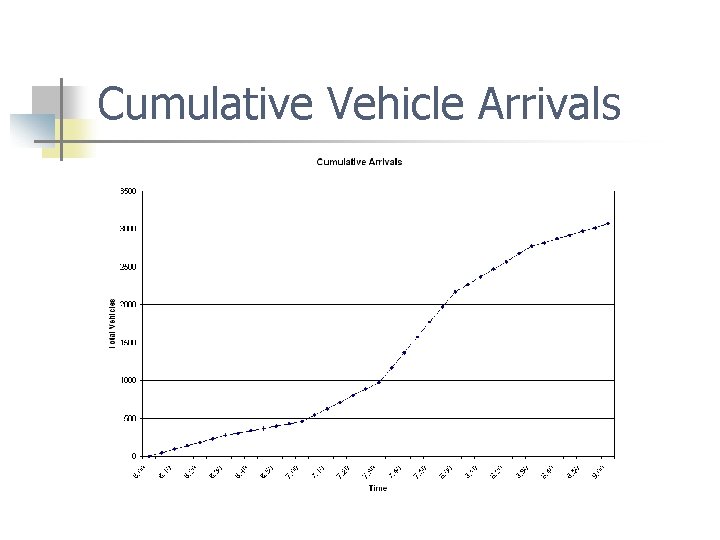
Cumulative Vehicle Arrivals

Modeling Employee Arrival Rates n First choice n n n Exponential distribution with user-defined mean Change it every 30 minutes Wrong! n n Good if rate change between periods is small Bad if rate change between periods is large

Modeling Employee Arrival Rates n Nonstationary Poisson Process (NSPP) n n Events occur one at a time Independent occurrences Expected rate over [t 1, t 2] Piecewise-constant rate function

NSPP using Thinning Method n Exponential distribution n n Generation Rate Lambda >= Maximum Rate Lambda Accepts/Rejects entities n n n 30 min period when entity created Expected arrival rate for that period Probability of Accepting Generated Entity Expected Arrival Rate Generation Rate

Carpooling n Discrete function n Virginia n n 60% - 1 person 25% - 2 people 10% - 4 people 5% - 6 people ~3000 vehicles n Maryland n n 75% - 1 person 15% - 2 people 5% - 4 people 5% - 6 people

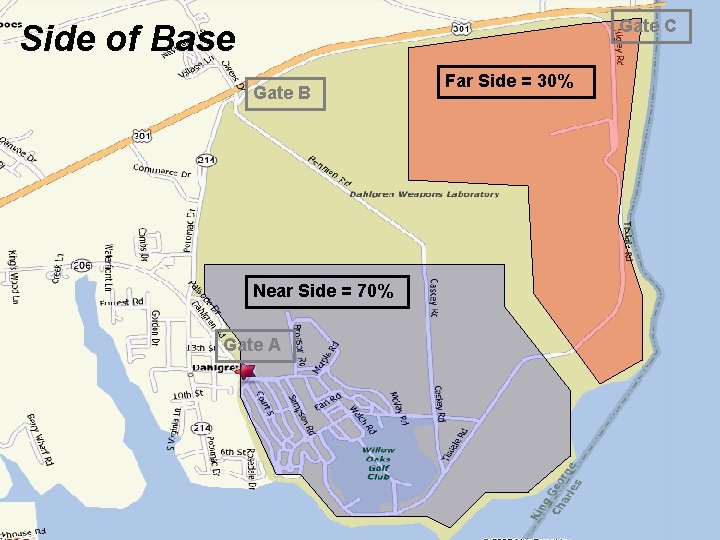
Gate C Side of Base Gate B Near Side = 70% Gate A Far Side = 30%

Gate Choice Gate B Near Side = 70% Gate A Far Side = 30%

Gate Delay = MIN(GAMMA(People. In. Vehicle * Badge. Time/Alpha, Alpha), Max. Delay) ____________________ n GAMMA (Beta, Alpha) n n n α=2 μ = αβ = α(People. In. Vehicle * Badge. Time) β = (People. In. Vehicle * Badge. Time) α Max. Delay = 360 seconds or 6 minutes

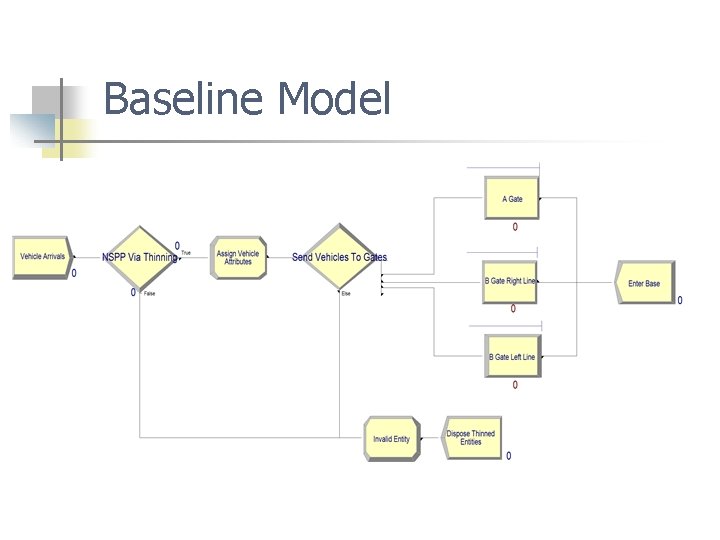
Baseline Model

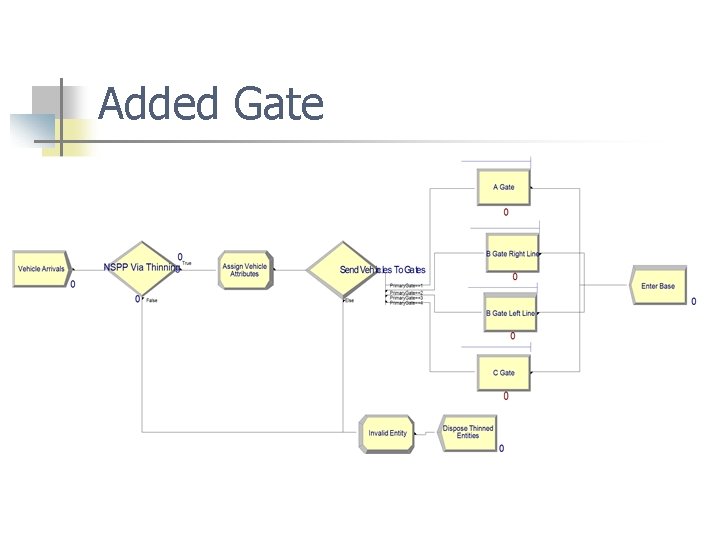
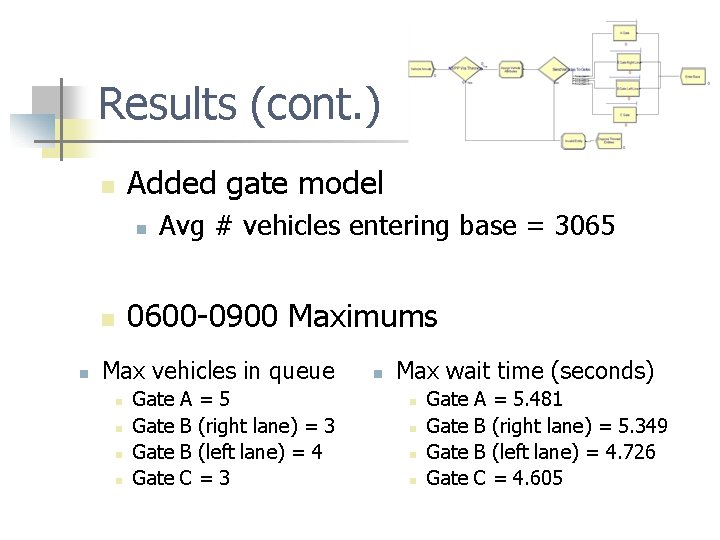
Added Gate

Batching Results n n n Temporal-based batching 5 minutes per batch 2 significant time periods (due to queues emptying during 0630 -0700 time frame) n 0600 -0700 n n Removed initial 10 minutes (before queue becomes significant) 0700 -0900 n Removed initial 5 minutes (before queue becomes significant)

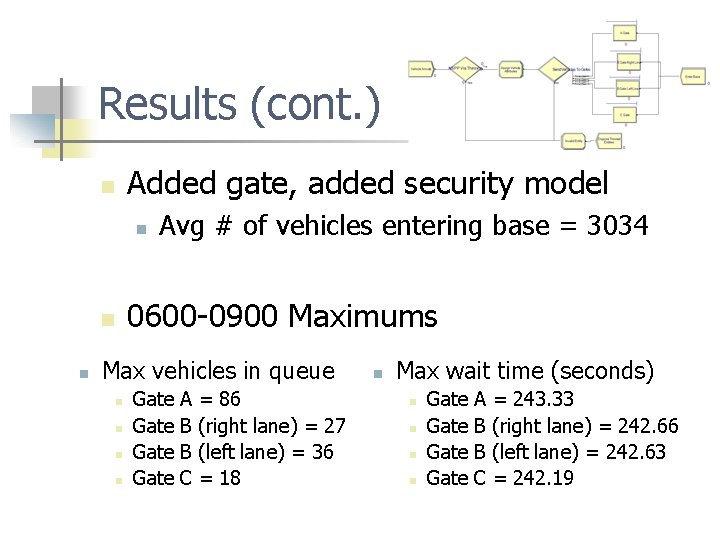
Baseline – Gates A & B Added Security – Gates A & B Added Gate – Gates A, B, & C Added Security – Gates A, B, & C

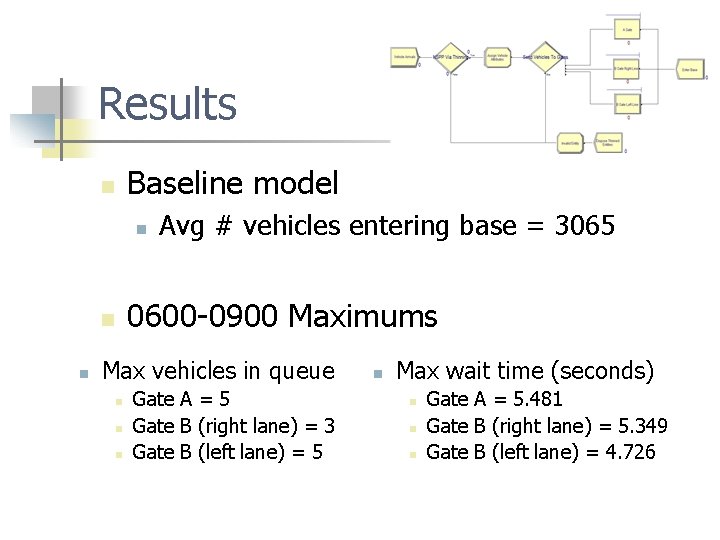
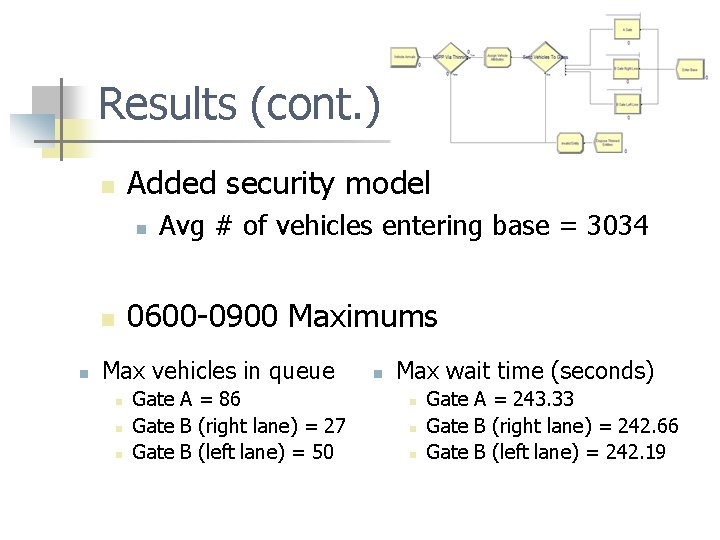
Results Baseline model n n 0600 -0900 Maximums n n Avg # vehicles entering base = 3065 Max vehicles in queue n n n Gate A = 5 Gate B (right lane) = 3 Gate B (left lane) = 5 n Max wait time (seconds) n n n Gate A = 5. 481 Gate B (right lane) = 5. 349 Gate B (left lane) = 4. 726

Results (cont. ) Added security model n n 0600 -0900 Maximums n n Avg # of vehicles entering base = 3034 Max vehicles in queue n n n Gate A = 86 Gate B (right lane) = 27 Gate B (left lane) = 50 n Max wait time (seconds) n n n Gate A = 243. 33 Gate B (right lane) = 242. 66 Gate B (left lane) = 242. 19

Results (cont. ) Added gate model n n 0600 -0900 Maximums n n Avg # vehicles entering base = 3065 Max vehicles in queue n n Gate A B B C =5 (right lane) = 3 (left lane) = 4 =3 n Max wait time (seconds) n n Gate A B B C = 5. 481 (right lane) = 5. 349 (left lane) = 4. 726 = 4. 605

Results (cont. ) Added gate, added security model n n 0600 -0900 Maximums n n Avg # of vehicles entering base = 3034 Max vehicles in queue n n Gate A B B C = 86 (right lane) = 27 (left lane) = 36 = 18 n Max wait time (seconds) n n Gate A B B C = 243. 33 (right lane) = 242. 66 (left lane) = 242. 63 = 242. 19

Running Tests n n 50 Replications Compared n n n Hypothesis testing n n n Wait times at the gates Number of cars in line at the gates 95% confidence interval Single tail test, talpha = (1. 671 + 1. 684)/2 = 1. 6775

Hypothesis of Wait Times (seconds) n n n n H 0: μgate A, Ha: μgate A, =1 baseline < 1 baseline H 0: (μgate A, Ha: (μgate A, – μgate A, added security – μgate A, H 0: (μgate B, Ha: (μgate B, – μgate B, added security, added gate – μgate B, =0 added security) < 0 H 0: (μgate C, Ha: (μgate C, – μgate C, added security, added gate – μgate C, added gate) added security baseline) =0 baseline) > 0 added security, added gate added security) =0 added gate) > 0

Example Calculation Analysis of Wait Times n Gate A – Baseline model – n X = 0. 004572 seconds ^ n σ = 0. 008355 seconds – Z=X –μ ^ σ / n -zα < Z to Reject H 0 Z = 0. 004572 – 1 Z = - 842. 4479 0. 008355/7. 071 - 842. 45 < -0. 16775 Z = -842. 4479 Reject H 0

Hypothesis of Vehicles in Line n n n n H 0: μgate A, Ha: μgate A, =1 baseline < 1 baseline H 0: (μgate A, Ha: (μgate A, – μgate A, added security – μgate A, H 0: (μgate B, Ha: (μgate B, – μgate B, added security, added gate – μgate B, =0 added security) < 0 H 0: (μgate C, Ha: (μgate C, – μgate C, added security, added gate – μgate C, added gate) added security baseline) =0 baseline) > 0 added security, added gate added security) =0 added gate) > 0

Example Calculation Analysis of Vehicles in Line n Added security model – Gate A compared to baseline mode – Gate A – n d = μ 1 – μ 2 = 12. 185 vehicles n σd= 23. 27 vehicles – T = d – D 0 σd / n tα < T to Reject H 0 T = 3. 7025 T = 12. 185 – 0 3. 7025 > 1. 6775 23. 27/7. 071 T = 3. 7025 Reject H 0

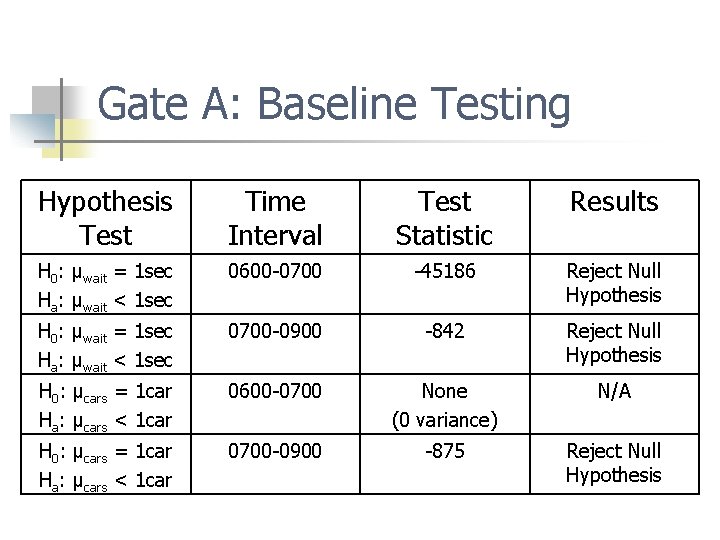
Gate A: Baseline Testing Hypothesis Test Time Interval Test Statistic Results H 0: μwait = 1 sec Ha: μwait < 1 sec 0600 -0700 -45186 Reject Null Hypothesis H 0: μwait = 1 sec Ha: μwait < 1 sec 0700 -0900 -842 Reject Null Hypothesis H 0: μcars = 1 car Ha: μcars < 1 car 0600 -0700 None (0 variance) N/A H 0: μcars = 1 car Ha: μcars < 1 car 0700 -0900 -875 Reject Null Hypothesis

Gate A w/Security Compared to Gate A Baseline Hypothesis Test Time Test Interval Statistic Results H 0: μwait, w/ security - μwait, baseline = 0 Ha: μwait, w/ security - μwait, baseline > 0 0600 -0700 6. 414 Reject Null Hypothesis H 0: μwait, w/ security - μwait, baseline = 0 Ha: μwait, w/ security - μwait, baseline > 0 0700 -0900 3. 614 Reject Null Hypothesis H 0: μcars, w/ security - μcars, baseline = 0 0600 -0700 Ha: μcars, w/ security - μcars, baseline > 0 4. 103 Reject Null Hypothesis

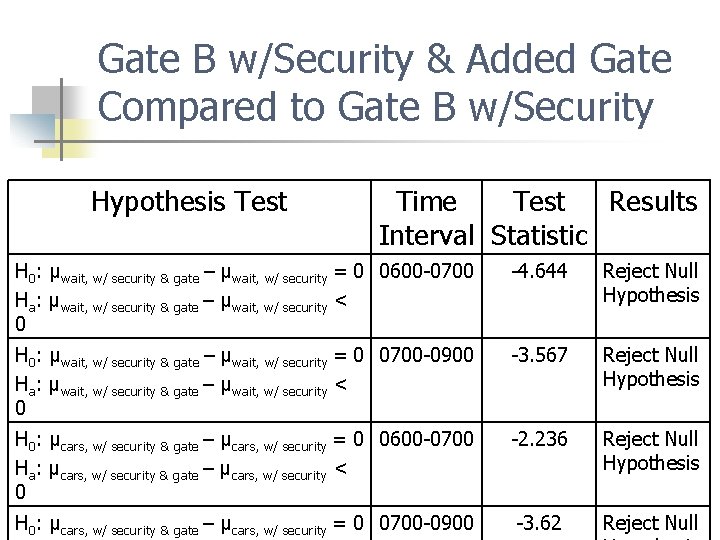
Gate B w/Security & Added Gate Compared to Gate B w/Security Hypothesis Test Time Test Results Interval Statistic H 0: μwait, w/ security & gate – μwait, w/ security = 0 0600 -0700 Ha: μwait, w/ security & gate – μwait, w/ security < 0 -4. 644 Reject Null Hypothesis H 0: μwait, w/ security & gate – μwait, w/ security = 0 0700 -0900 Ha: μwait, w/ security & gate – μwait, w/ security < 0 -3. 567 Reject Null Hypothesis H 0: μcars, w/ security & gate – μcars, w/ security = 0 0600 -0700 Ha: μcars, w/ security & gate – μcars, w/ security < 0 -2. 236 Reject Null Hypothesis H 0: μcars, w/ security & gate – μcars, w/ security = 0 0700 -0900 -3. 62 Reject Null

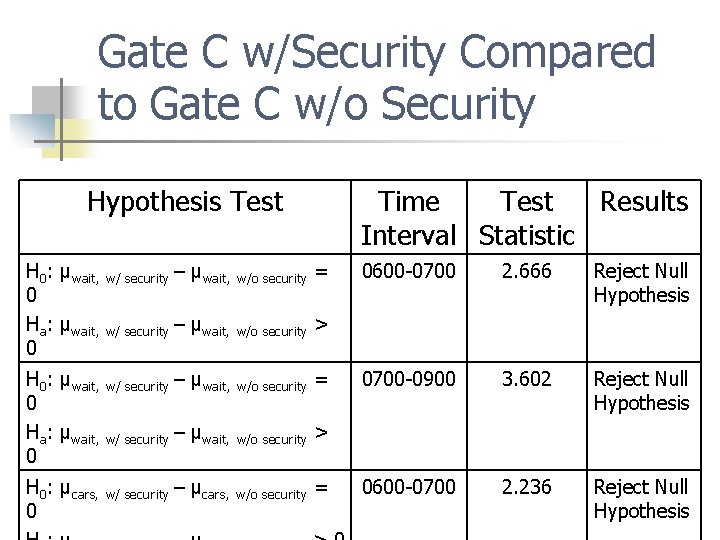
Gate C w/Security Compared to Gate C w/o Security Hypothesis Test Time Test Results Interval Statistic H 0: μwait, w/ security – μwait, w/o security = 0 Ha: μwait, w/ security – μwait, w/o security > 0 0600 -0700 2. 666 Reject Null Hypothesis H 0: μwait, w/ security – μwait, w/o security = 0 Ha: μwait, w/ security – μwait, w/o security > 0 0700 -0900 3. 602 Reject Null Hypothesis H 0: μcars, 0 0600 -0700 2. 236 Reject Null Hypothesis w/ security – μcars, w/o security =

Lessons Learned n n Like to get exact census data Hypothesis testing for a defined increase in wait time or vehicles in line n n n Thinning method is very helpful Possible improvements would include traffic patterns to control gate entry n n H 0: μwait, w/ security – μwait, w/o security = N Gate C Unavailable to South-bound traffic Comparison of Dahlgren Base entry to other government installations