Simulated Evolution Algorithm for Multi Objective VLSI Netlist

Simulated Evolution Algorithm for Multi. Objective VLSI Netlist Bi-Partitioning Sadiq M. Sait, Aiman El-Maleh, Raslan Al-Abaji King Fahd University of Petroleum & Minerals Dhahran, Saudi Arabia 27 th May, ISCAS-2003, Bangkok, Thailand

Outline § § § Introduction Problem Formulation Cost Functions Proposed Approach Experimental Results Conclusion 2

VLSI Technology Trends Design Characteristics 0. 06 M 2 MHz 6 um SPICE Simulation 0. 13 M 12 MHz 1. 5 um CAE Systems, Silicon Compilation 1. 2 M 50 MHz 0. 8 um HDLs, Synthesis 3. 3 M 200 MHz 0. 6 um Top-Down Design, Emulation 7. 5 M 333 MHz 0. 25 um Cycle-Based Simulation, Formal Verification Key CAD Capabilities The challenges to sustain such a fast growth to achieve giga-scale integration have shifted in a large degree, from the process of manufacturing technologies to the design technology. New issues have also come up. 3

VLSI Design Cycle VLSI design process comprises a number of levels: 1. 2. 3. 4. 5. 6. 7. 8. System Specification Functional Design Logic Design Circuit Design Physical Design Verification Fabrication Packaging Testing and Debugging 4

Physical Design What is Physical Design? A process that translates a structural (netlist) description into a geometric description that is used to manufacture a chip. The physical design cycle consists of: 1. Partitioning 2. Floorplanning and Placement 3. Routing 4. Compaction Why do we need Partitioning ? 5

Levels of Partitioning System Level Partitioning PCBs Board Level Partitioning Chips Subcircuits /Blocks 6

Classification of Partitioning Algorithms Group Migration 1. Kernighan-Lin 2. Fiduccia. Mattheyeses (FM) 3. Multilevel K -way Partitioning Iterative Heuristics 1. Simulated Annealing 2. Simulated Evolution 3. Tabu Search 4. Genetic Algorithm Performance Driven Others 1. Lawler et al. 1. Spectral 2. Vaishnav 3. Choi et al. 4. Jun’ichiro et al. 2. Multilevel Spectral 7

Related previous Work 1969 A bottom-up approach for delay optimization (clustering) was proposed by Lawler et al. 1998 A circuit partitioning algorithm under path delay constraint is proposed by jun’ichiro et al. The proposed algorithm consists of the clustering and iterative improvement phases. 1999 Two low power oriented techniques based on simulated annealing (SA) algorithm by choi et al. 1999 Enumerative partitioning algorithm targeting low power were proposed by Vaishnav et al. Enumerates alternate partitioning and selects a partitioning that has the same delay but less power dissipation. 8

Motivation & Objective Need for Power optimization: § Portable devices § Power consumption is a hindrance to further integration § Increasing clock frequency Need for Delay optimization: § In current sub micron design wire delays tend to dominate gate delay. § Larger die size imply long on-chip wires which affect performance § Delay due to off-chip capacitance Objectives: Power, Delay & Cutset are optimized Constraint: Balanced partitions (with some tolerance) 9

Problem formulation n The circuit is modeled as a hypergraph H(V, E), where V={v 1, v 2, v 3, … vn} is a set of modules (cells) And E={e 1, e 2, e 3, … ek} is a set of hyperedges. Being the set of signal nets, each net is a subset of V containing the modules that the net connects. A 2 -way partitioning of a set of nodes V is to determine subsets VA and VB such that VA VB = V and VA VB = 10

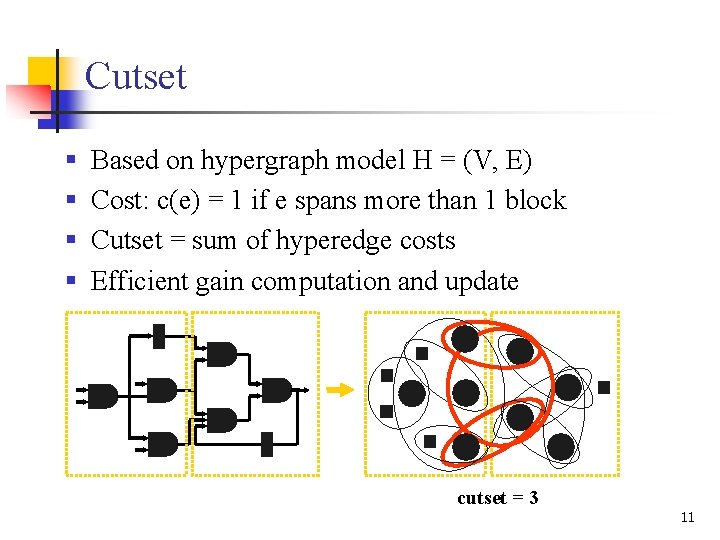
Cutset § § Based on hypergraph model H = (V, E) Cost: c(e) = 1 if e spans more than 1 block Cutset = sum of hyperedge costs Efficient gain computation and update cutset = 3 11

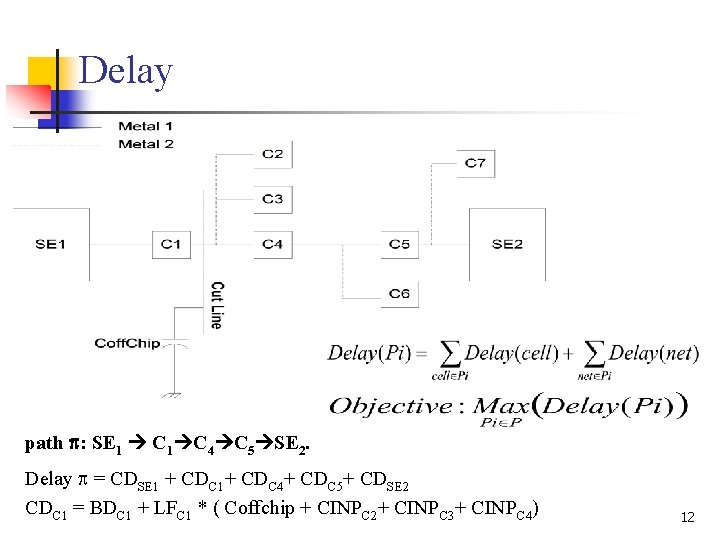
Delay path : SE 1 C 1 C 4 C 5 SE 2. Delay = CDSE 1 + CDC 1+ CDC 4+ CDC 5+ CDSE 2 CDC 1 = BDC 1 + LFC 1 * ( Coffchip + CINPC 2+ CINPC 3+ CINPC 4) 12

Power The average dynamic power consumed by CMOS logic gate in a synchronous circuit is given by: Ni is the number of output gate transition per cycle (Switching Probability) load capacitance = Load Capacitances before Partitioning + load due to off chip capacitance Total Power dissipation of a Circuit: 13

Unifying Objectives by Fuzzy logic Weighted Sum Approach 1. Problems in choosing weights 2. Need to tune for every circuit § Imprecise values of the objectives §Best represented by linguistic terms that are basis of fuzzy algebra § Conflicting objectives § Operators for aggregating function 14

Fuzzy logic for Multi-objective function 1. The cost to membership mapping 2. Linguistic fuzzy rule for combining the membership values in an aggregating function 3. Translation of the linguistic rule in form of appropriate fuzzy operators 4. Fuzzy operators • And-like operators: Min operator = min ( 1, 2) • And-like OWA: = * min ( 1, 2) + ½ (1 - ) ( 1+ 2) • Or-like operators: Max operator = max ( 1, 2) • Or-like OWA: = * max ( 1, 2) + ½ (1 - ) ( 1+ 2) Where is a constant in range [0, 1] 15

Membership functions Where Oi and Ci are lower bound actual cost of objective “i” i(x) is the membership of solution x in set “good ‘i’ gi is the relative acceptance limit for each objective. 16

Fuzzy linguistic rule & Cost function A good partitioning can be described by the following fuzzy rule IF solution has small cutset AND low power AND short delay AND good Balance THEN it is a good solution The above rule is translated to AND-like OWA Represent the total Fuzzy fitness of the solution, our aim is to Maximize this fitness Respectively (Cutset, Power, Delay, Balance) Fitness 17

Simulated Evolution Algorithm Simulated_Evolution Begin Start with an initial feasible Partition S Repeat Evaluation: Evaluate Gi (goodness) for all modules Selection: For each Vi (cell) DO begin if Random Rm > Gi then select the cell End For Allocation: For each selected Vi (cell) DO begin Move the cell to destination block. End For Until Stopping criteria is satisfied. Return best solution. End 18

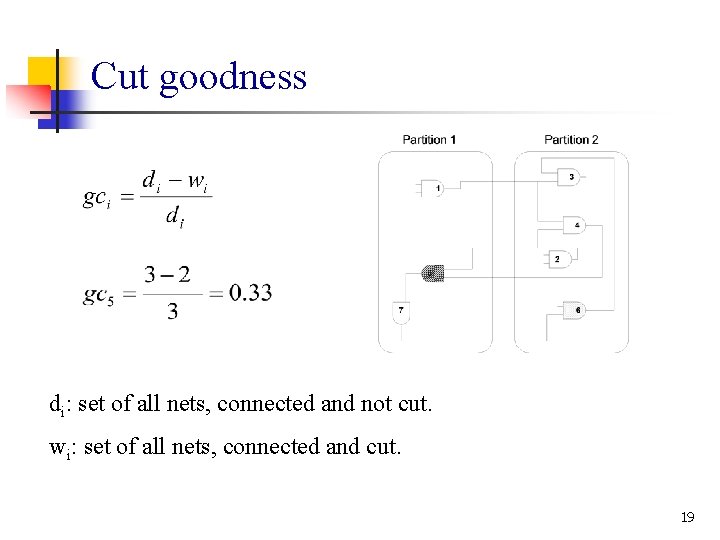
Cut goodness di: set of all nets, connected and not cut. wi: set of all nets, connected and cut. 19

Power Goodness Vi is the set of all nets connected and Ui is the set of all nets connected and cut. 20

Delay Goodness Ki: is the set of cells in all paths passing by cell i. Li: is the set of cells in all paths passing by cell i and are not in same block as i. 21

Final selection Fuzzy rule IF cell ‘i’ is near its optimal cut-set goodness as compared to other cells near its optimal power goodness AND compared to other cells near its optimal net delay goodness as compared to other cells AND OR T(max)(i) is much smaller than Tmax THEN it has a high goodness. 22

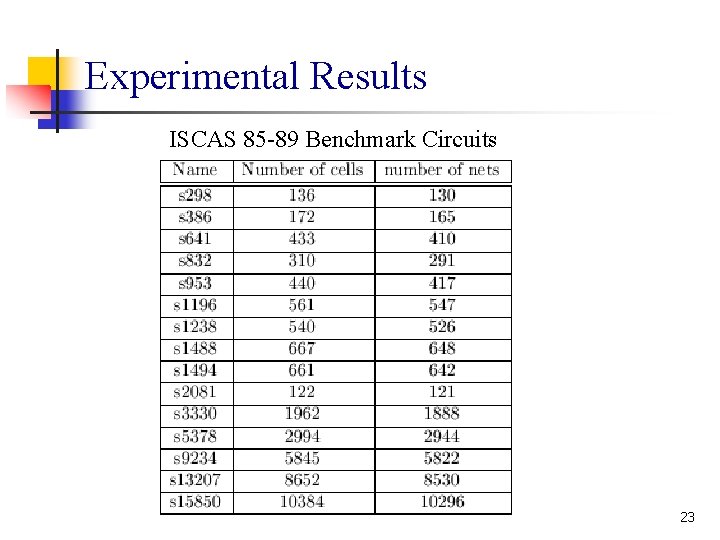
Experimental Results ISCAS 85 -89 Benchmark Circuits 23

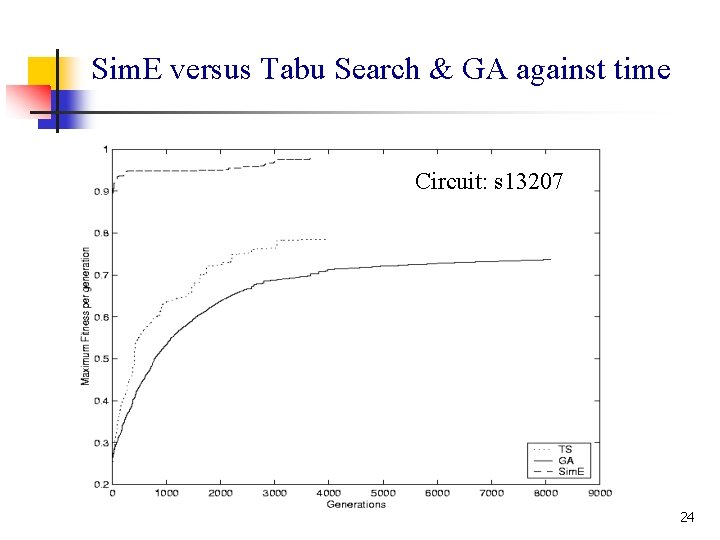
Sim. E versus Tabu Search & GA against time Circuit: s 13207 24

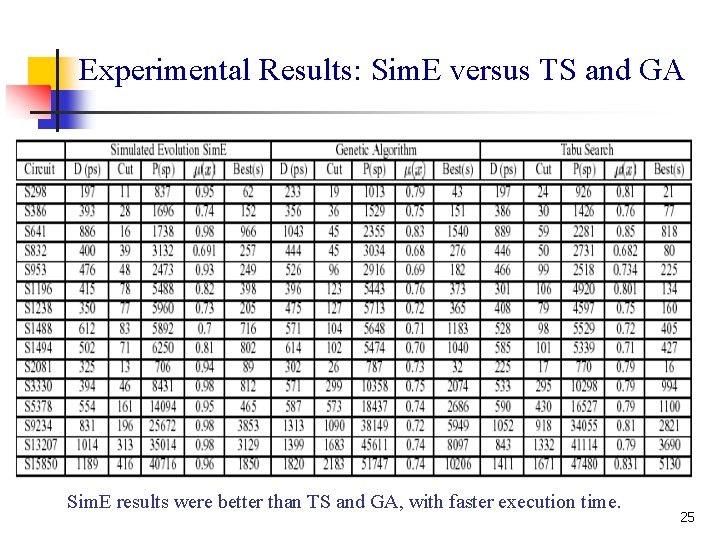
Experimental Results: Sim. E versus TS and GA Sim. E results were better than TS and GA, with faster execution time. 25

Conclusion n n The present work addressed the issue of partitioning VLSI circuits with the objective of reducing power and delay (in addition to nets cut) Fuzzy logic was resorted to for combining multiobjectives Iterative algorithms (GA, SA, and Sim. E) were investigated and compared for performance in terms of quality of solution and run time Sim. E outperformed TS and GA in terms of quality of solution and execution time 26

Thank you 27

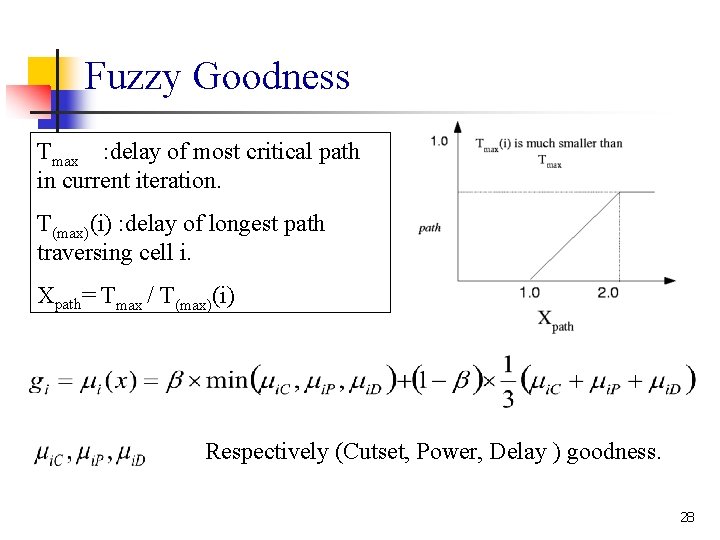
Fuzzy Goodness Tmax : delay of most critical path in current iteration. T(max)(i) : delay of longest path traversing cell i. Xpath= Tmax / T(max)(i) Respectively (Cutset, Power, Delay ) goodness. 28