Simplifying Rational Expressions Lesson 11 1 Rational Expression

















































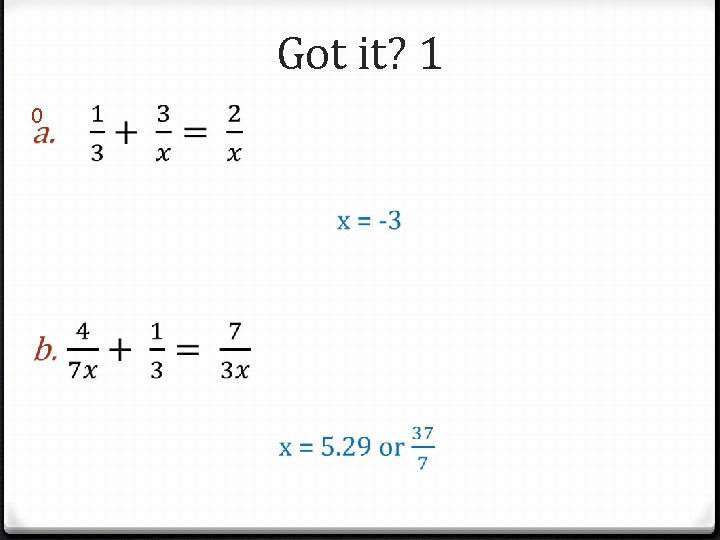




























- Slides: 86

Simplifying Rational Expressions Lesson 11 -1

Rational Expression 0

Problem 1 0

Got it? 1 0

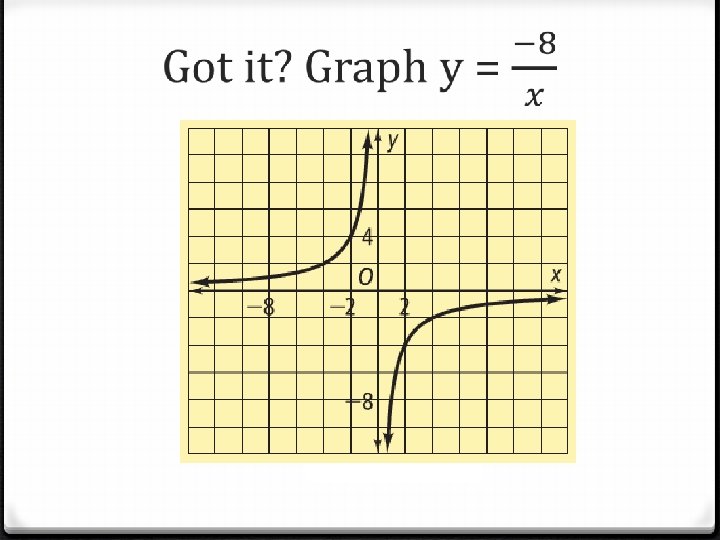
Problem 2 0

Got it? 2 Simplify and give the excluded values. 0

Opposite Numerators and Denominators 0

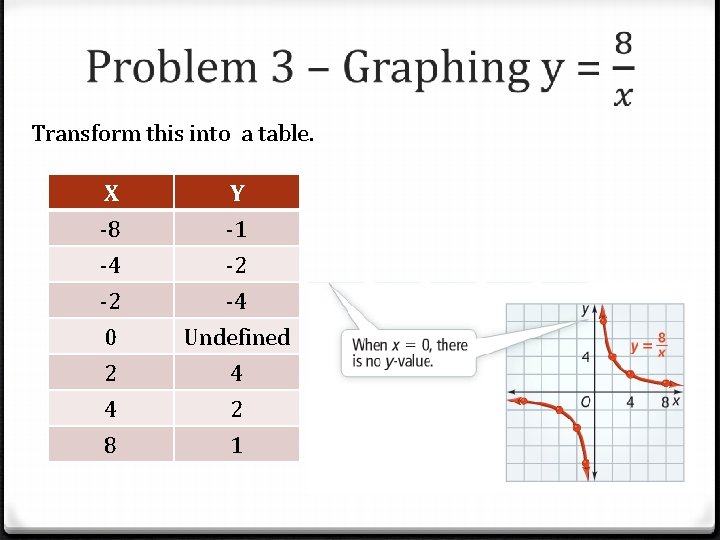
Problem 3 0

Problem 3 0

Problem 3 0

Got it? 3 0 -1, x ≠ -2. 5 -y – 4 , y ≠ 4

Problem 4 0

Complete #30 as a class.

Multiplying and Dividing Ra tional Expressions Lesson 11 -2

Key Concept 0

Problem 1: What is the product? 0

Problem 1: What is the product? 0

Got it? Find the product. 0

Problem 2: Using Factoring 0 2

Got it? Find the product 0

Problem 3: Multiplying by a Polynomial 0

Got it? 3 Multiply these expressions 0

Dividing Rational Expressions Step 1: Change the division sign to a multiplication sign. Step 2: Take the reciprocal of the second part. Step 3: Multiply and simplify.

Problem 4: Dividing Expressions 0

Problem 4: Got it? 0

Problem 5: Dividing Expressions 0

Problem 5: Got it? 0

Problem 6: Complex Expressions 0

Problem 6: Got it? 0

Dividing Polynomial s Lesson 11 -3

Problem 1: Dividing by a Monomial 0

Problem 1: Got it? 0

Problem 2: Dividing by a Binomial Compute 22 ÷ 5 using long division. You will have a remainder. Now try, (3 d 2 – 4 d + 13) ÷ (d + 3) on the board.

Problem 2: Got it? (2 m 2 – m + 3) ÷ (m + 1) Answer: 2 m – 3

Problem 3: Dividing with a Zero Coefficient The width w of a rectangle is 3 z – 1. The area A of the rectangle is 18 z 3 – 8 z + 2. What is an expression for the length? Step 1: We need to represent all of the degrees of z. 18 z 3 – 8 z + 2 = 18 z 3 + 0 z 2 – 8 z + 2 Use 18 z 3 + 0 z 2 – 8 z + 2 when dividing. Complete on the board.

Problem 3: Got it? 0

Problem 4: Reordering Terms before Dividing What is (-10 x – 1 + 4 x 2) ÷ (-3 + 2 x) Step 1: We need to reorder them from greatest to smallest degree. (-10 x – 1 + 4 x 2) = (4 x 2 – 10 x – 1) (-3 + 2 x) = (2 x – 3) Now Divide. Complete on the board.

Problem 4: Got it? 0

Adding and Subtracting Rational Expressions Lesson 11 -4

Review of adding and subtracting fractions: Remember? Like Denominators: add the numerator and keep the denominator the same. Difference Denominators: find the least common multiple and change the denominators so they look the same. Then add the numerators.

Problem 1 and 2: Adding and Subtracting with Like Denominators 0

Problem 1 and 2 Got it? 0

Problem 3: Adding with Unlike Denominators 0

Problem 3: Got it? 0

Problem 4: Subtracting with Unlike Denominators 0

Problem 4: Got it? 0

Solving Rat ional Equations Lesson 11 -5

Rational Equation 0

Problem 1 0
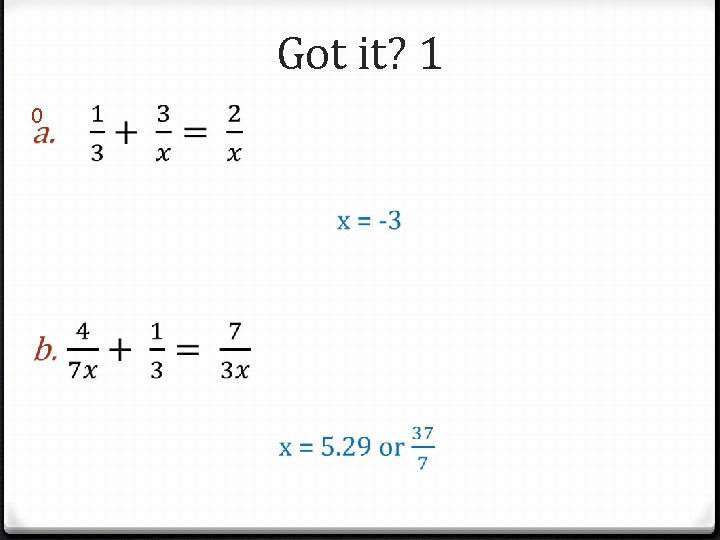
Got it? 1 0

Problem 2 0

Got it? 2 0

Problem 3 0

Problem 3 0

Got it? 3 0

Problem 4 0

Got it? 4 0

Problem 5 0

Problem 5 (Continued) 0

Got it? 5 0

Inverse Var iation Lesson 11 -6

Examples of Inverse Variation The more workers building a house, the less days it will be unlivable. The longer the board, the less strength you need to break it. The more roommates in an apartment, the less rent everyone has to pay. When one increase, the other decrease (and vice versa).

Inverse Variation in Math 0

Problem 1 0

Got it? 1 0

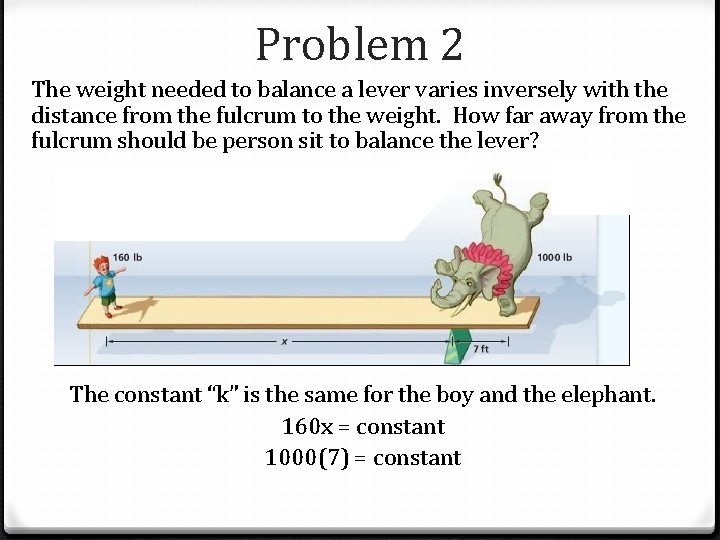
Problem 2 The weight needed to balance a lever varies inversely with the distance from the fulcrum to the weight. How far away from the fulcrum should be person sit to balance the lever? The constant “k” is the same for the boy and the elephant. 160 x = constant 1000(7) = constant

Problem 2 (continued) The weight needed to balance a lever varies inversely with the distance from the fulcrum to the weight. How far away from the fulcrum should be person sit to balance the lever? The constant “k” is the same for the boy and the elephant. 160 x = constant 1000(7) = constant 160 x = 7000 x = 43. 75 The boy should move 43. 75 from the fulcrum to balance the level.

Got it? 2 0 A 120 lb weight is placed on a lever, 5 feet from the fulcrum. How far from the fulcrum should an 80 lb weight be place to balance the lever? 120(5) = 80 x 600 = 80 x x = 7. 5 ft

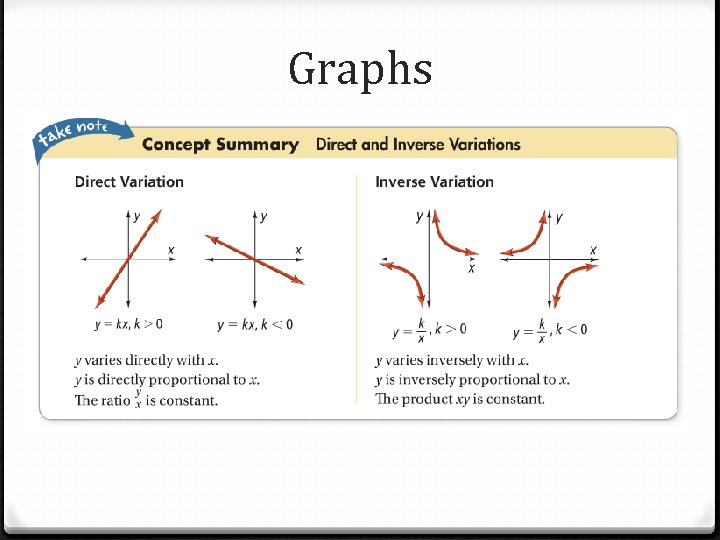
Graphs

Transform this into a table. X -8 -4 -2 Y -1 -2 -4 0 2 4 8 Undefined 4 2 1


Problem 4: Determining Inverse Variation 0 X 3 4 5 Y -15 -20 -25

Problem 4: Determining Inverse Variation What is the equation for this table? Direct variation formula is y = kx, where k is the constant. To find the constant divide y by x. In this case, k = -5. The equation is y = -5 x X 3 4 5 Y -15 -20 -25

Got it? 4 Does this show inverse or direct variation? Give the equation of the table. A. B. X 4 6 8 Y -12 -18 -24 X 4 6 8 Y -12 -8 -6 Direct; y = -3 x Inverse; xy = -48

Problem 5 – Real Life Does this situation show inverse or direct variation? a. The cost of a $120 boat rental is split among several friends. The more friends you have, the less each person has to pay. This is inverse variation. b. You download several movies for $14. 99 each. The more movies you buy, the more it will cost. This is direct variation.

Graphing R ational Functions Lesson 11 -7

Rational Functions 0

Problem 1: Finding excluded values 0

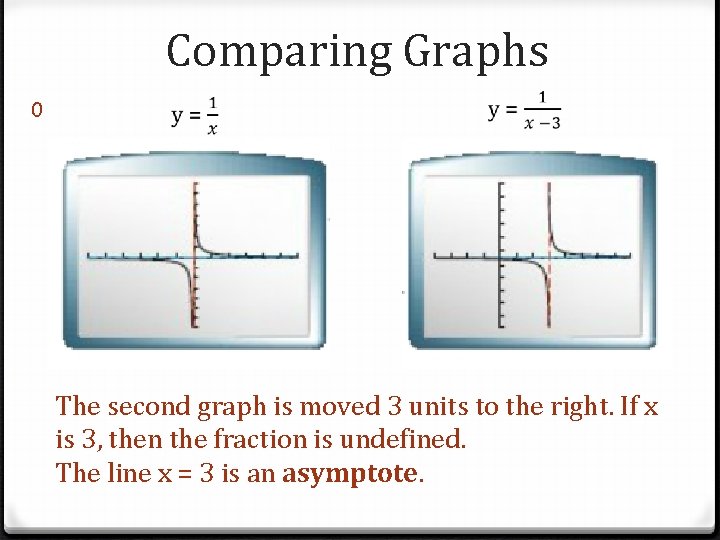
Comparing Graphs 0 The second graph is moved 3 units to the right. If x is 3, then the fraction is undefined. The line x = 3 is an asymptote.

Where is the asymptote? 0

Problem 2: Graphing with a Vertical Asymptote 0

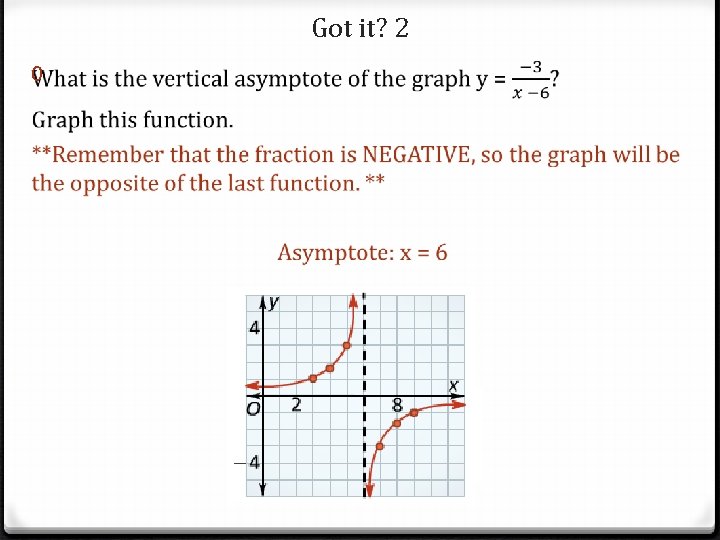
Got it? 2 0

Vertical and Horizontal Asymptotes: The graph can move right, left, UP and DOWN.

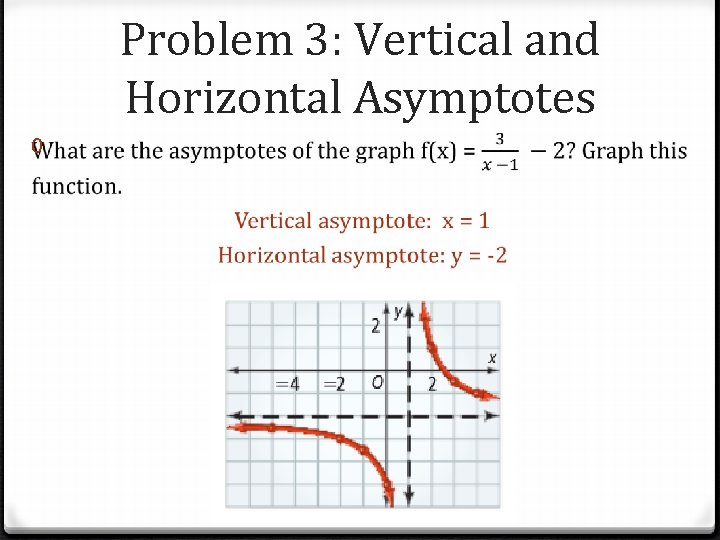
Problem 3: Vertical and Horizontal Asymptotes 0

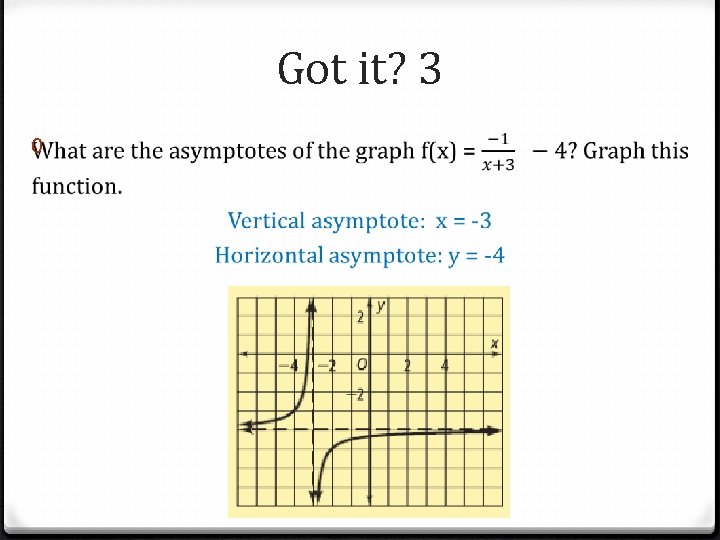
Got it? 3 0

In General… If the function is POSITIVE: the graph will be in quadrants 1 and 3. If the function is NEGATIVE: the graph will be in quadrants 2 and 4. Vertical asymptote is x = Horizontal asymptote is y =