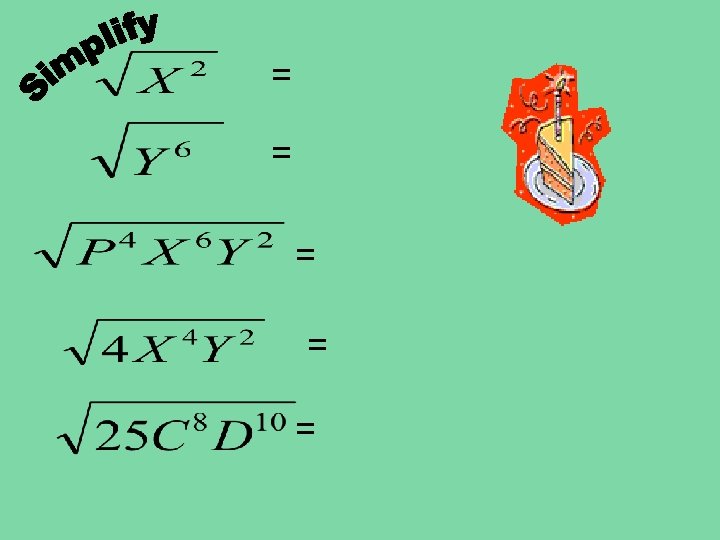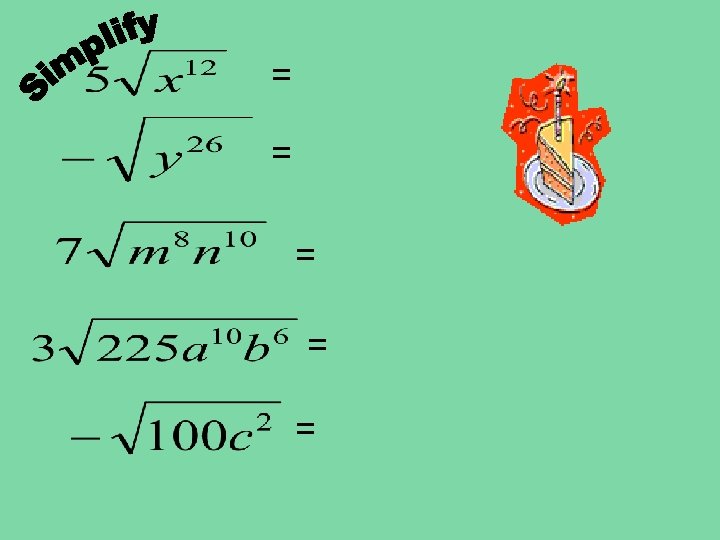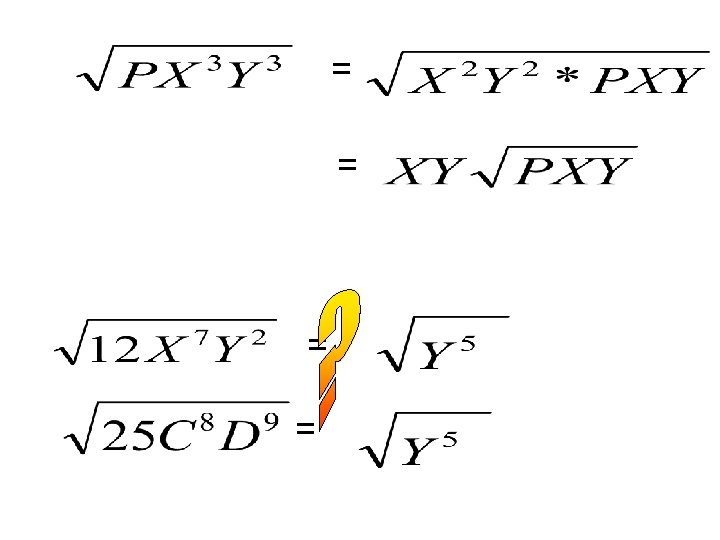Simplifying Radicals Perfect Squares 1 4 9 16




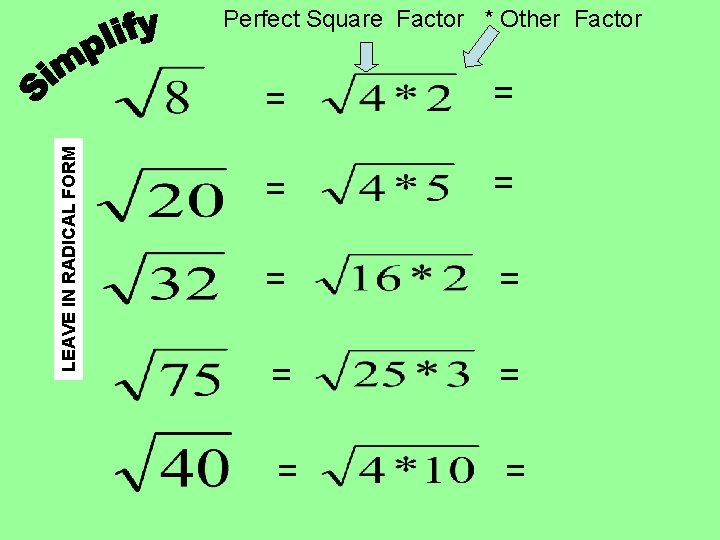
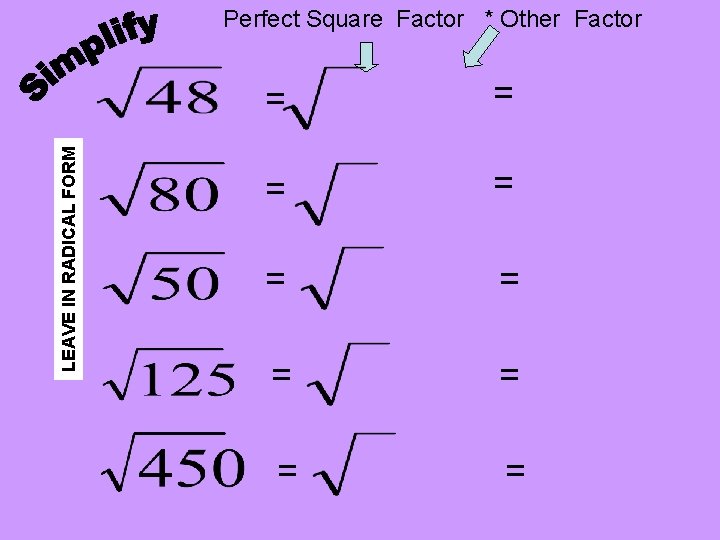
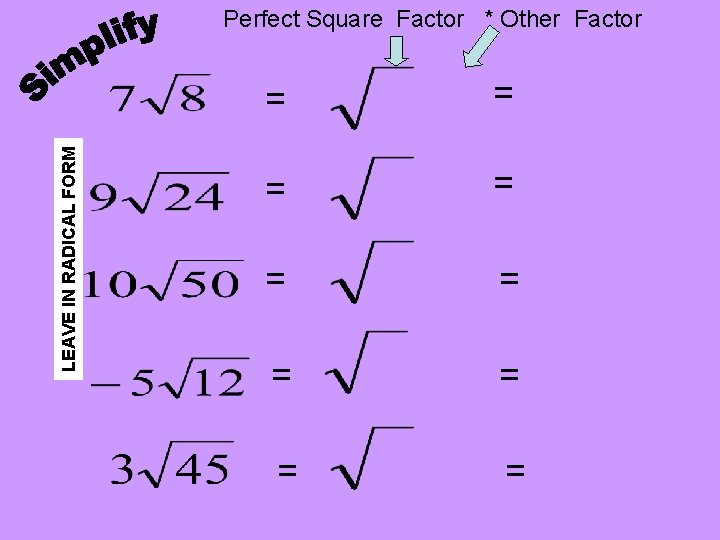
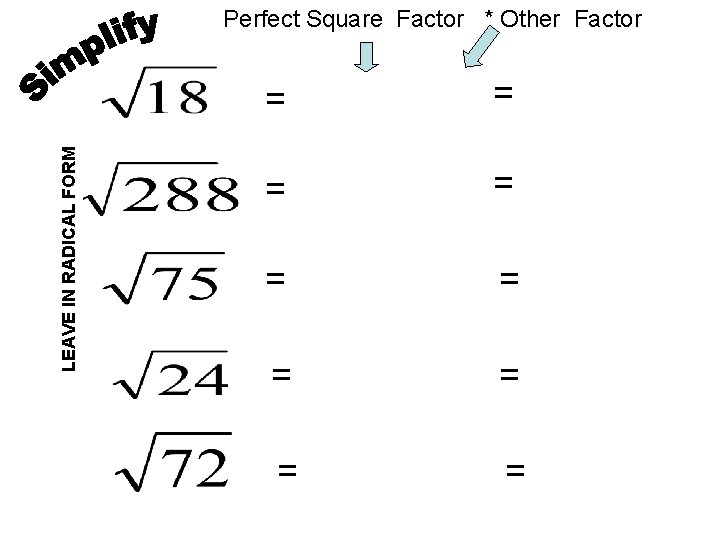


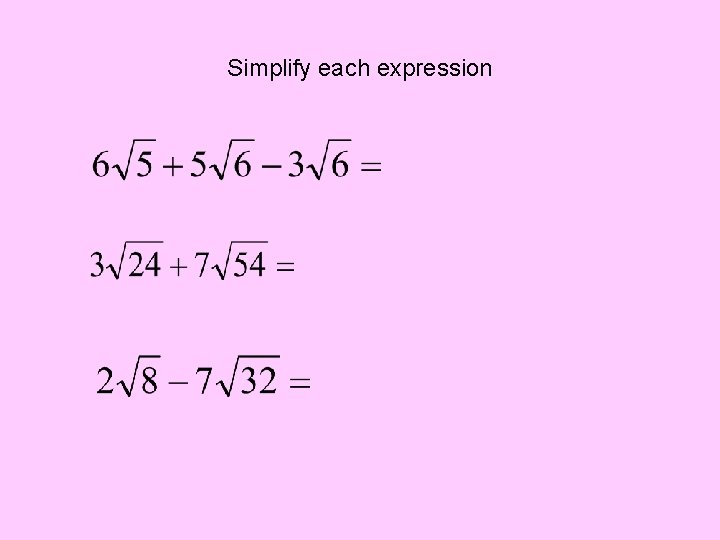
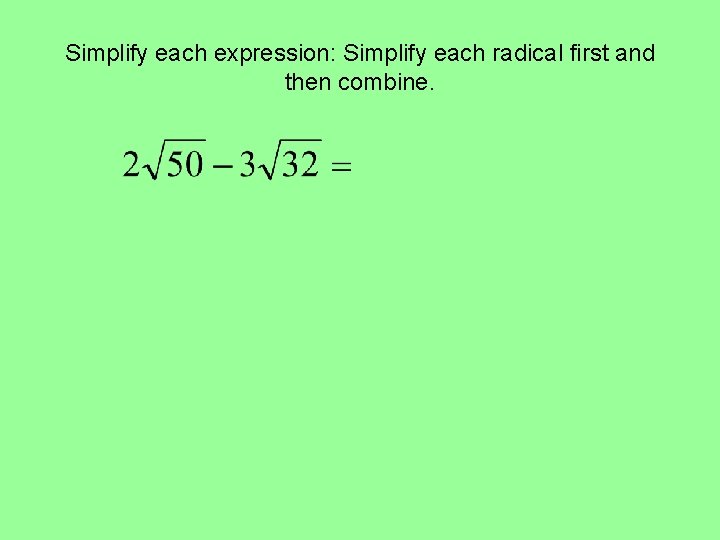


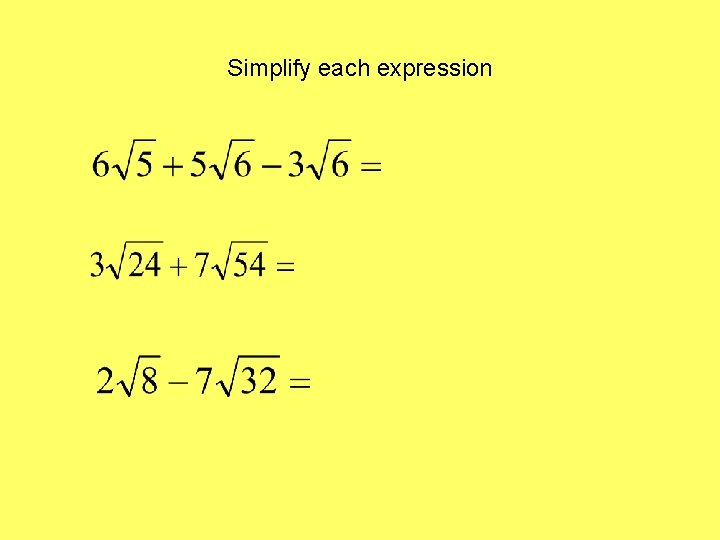
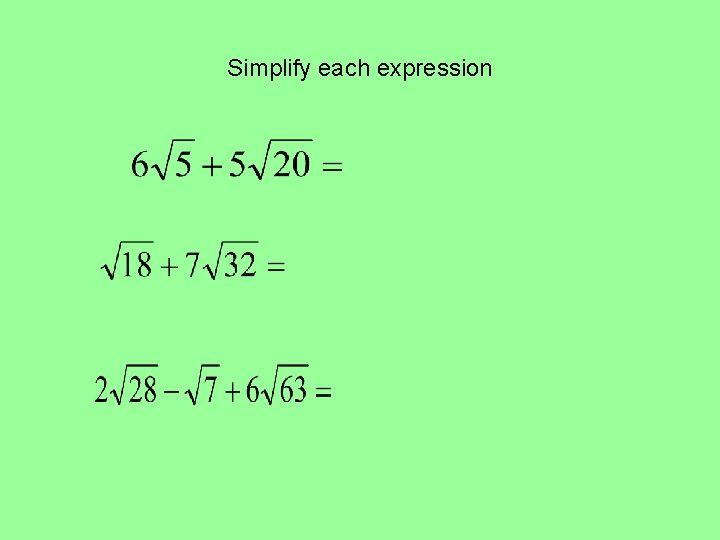

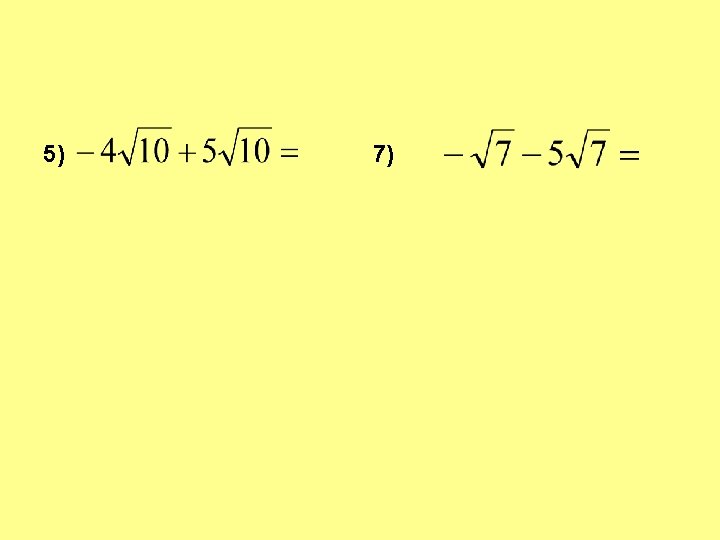

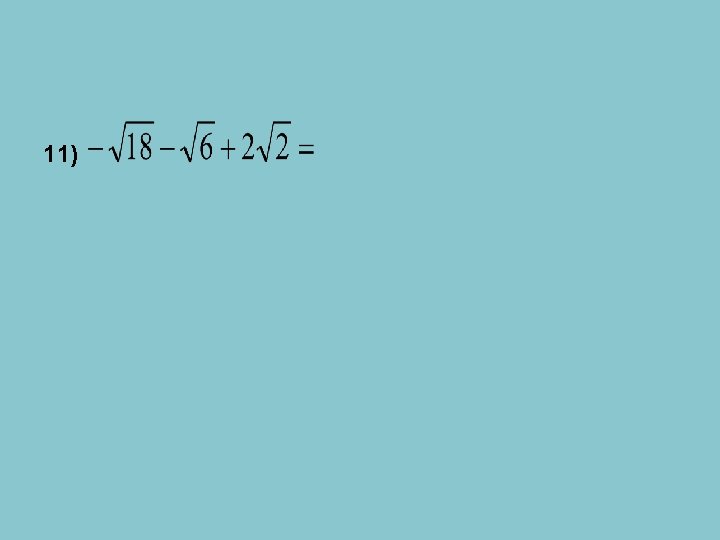
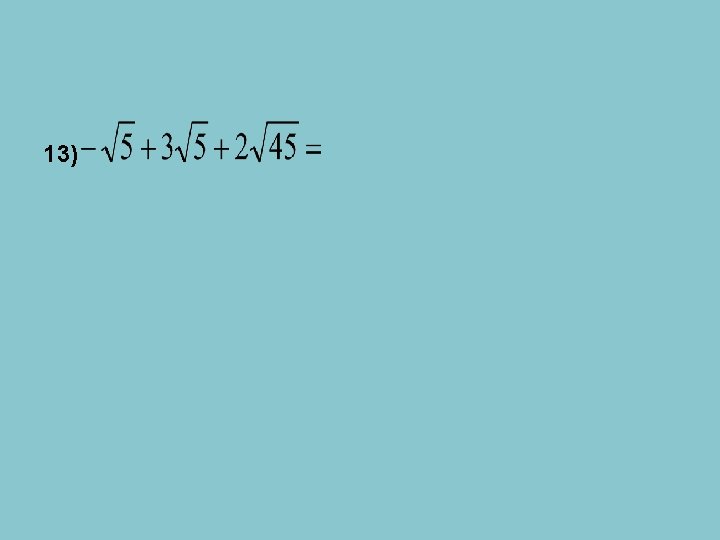
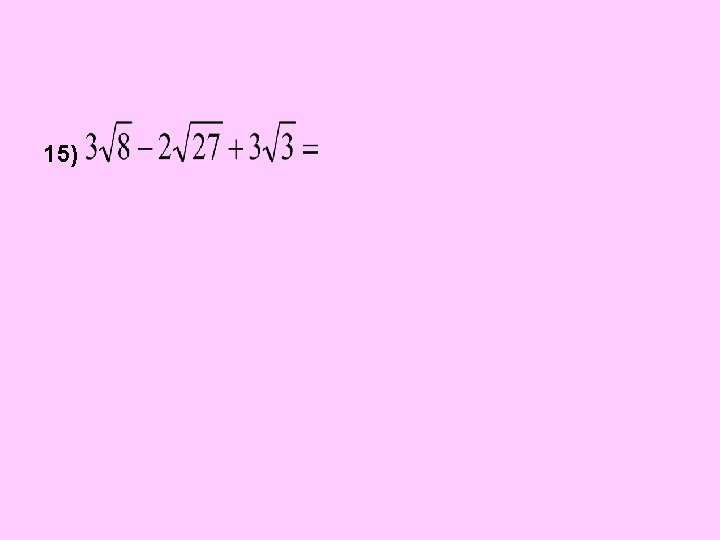
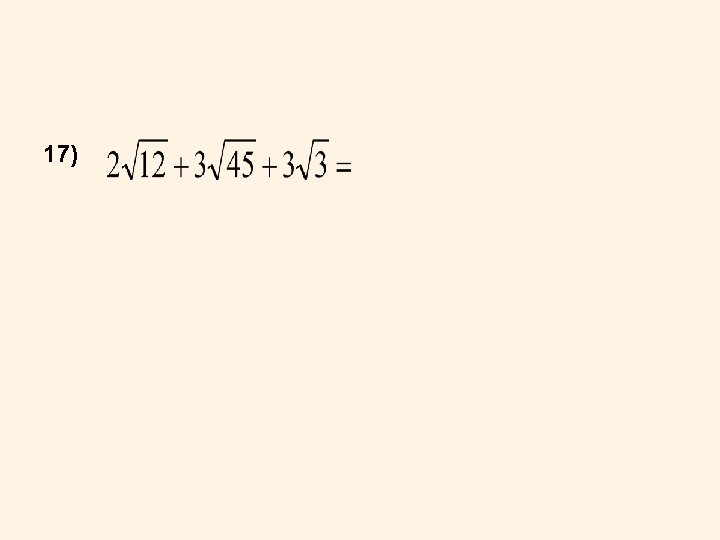



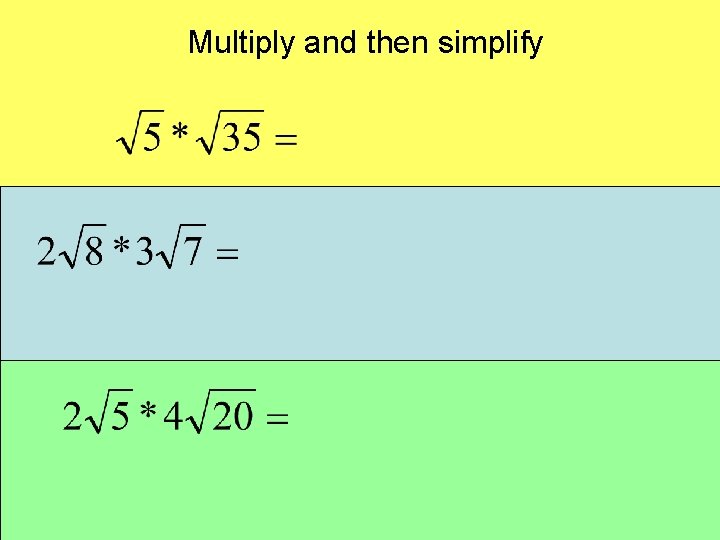

















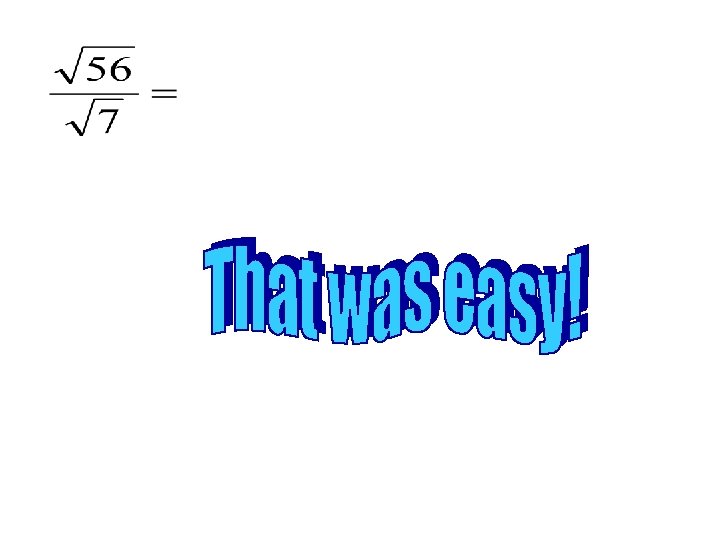


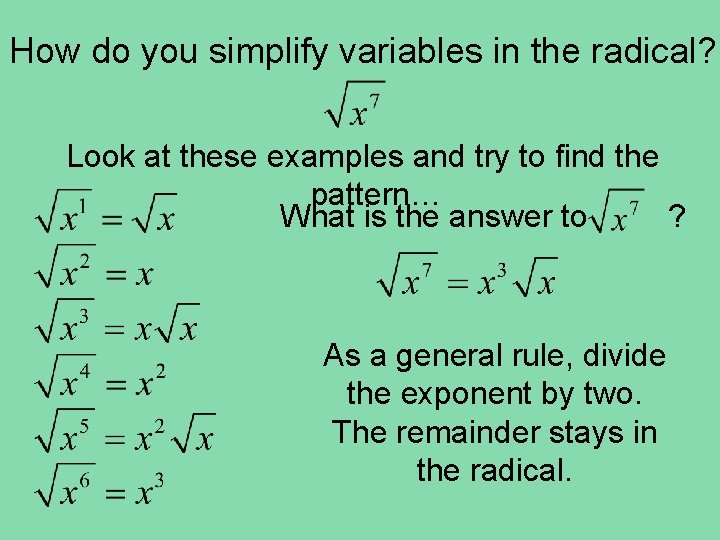

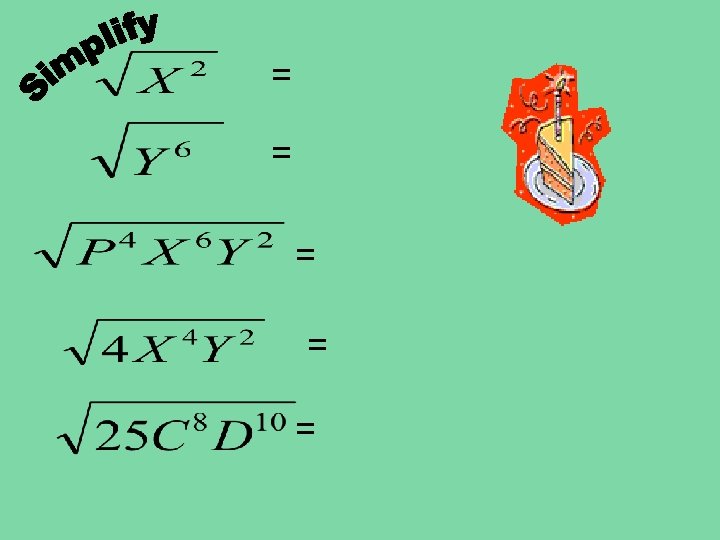
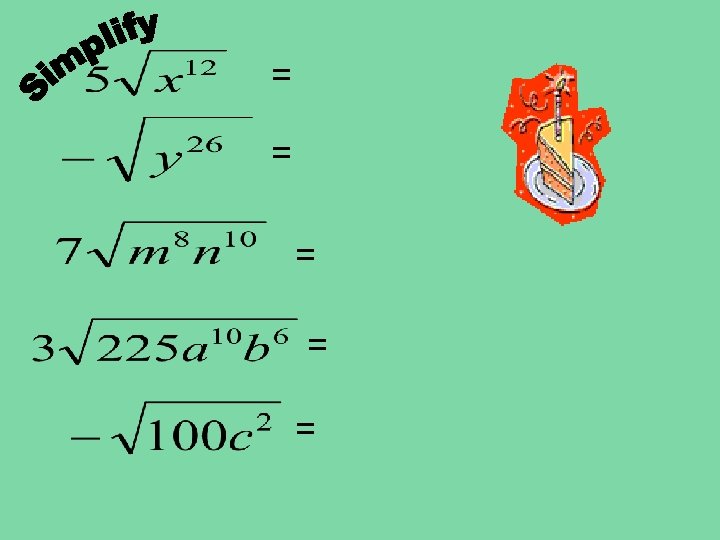

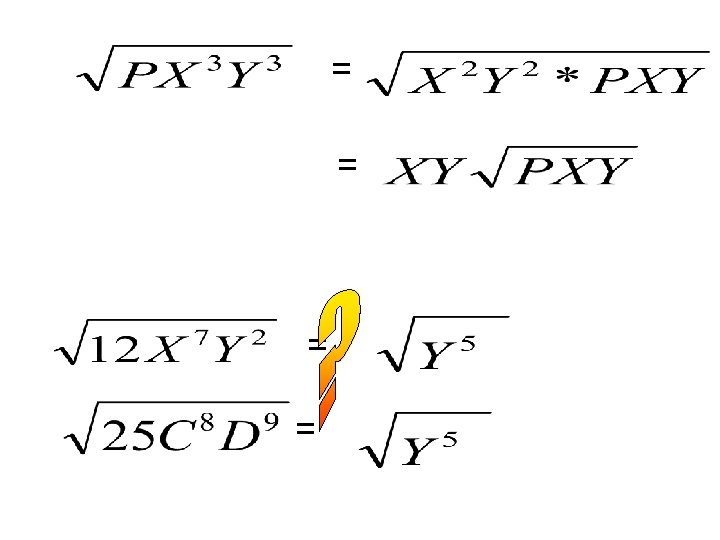
- Slides: 55

Simplifying Radicals

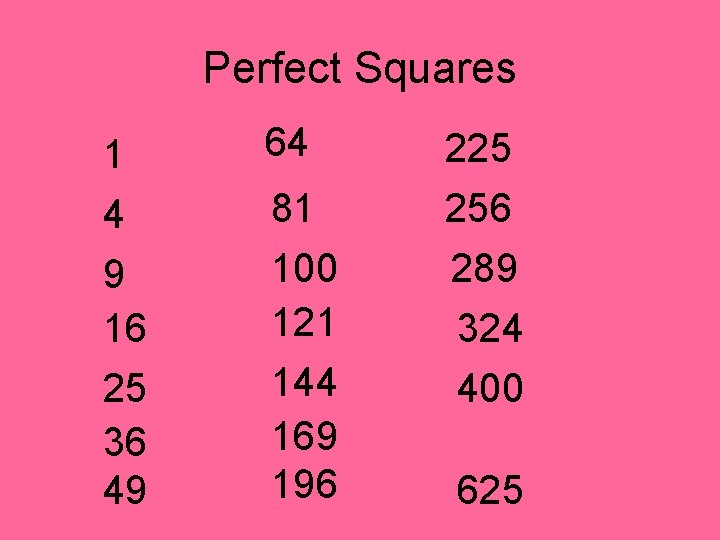
Perfect Squares 1 4 9 16 25 36 49 64 225 81 100 121 144 169 196 256 289 324 400 625

How do you simplify variables in the radical? Look at these examples and try to find the pattern… What is the answer to ? As a general rule, divide the exponent by two. The remainder stays in the radical.

Simplifying variable radicands • X² • X • X

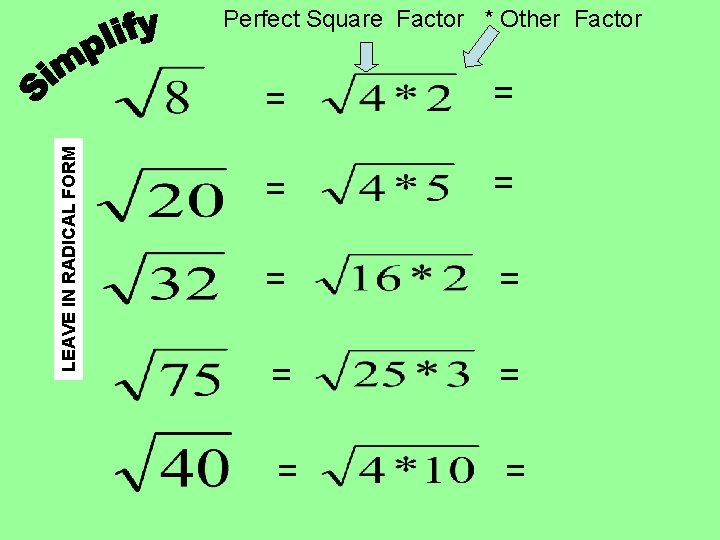
LEAVE IN RADICAL FORM Perfect Square Factor * Other Factor = = = = =
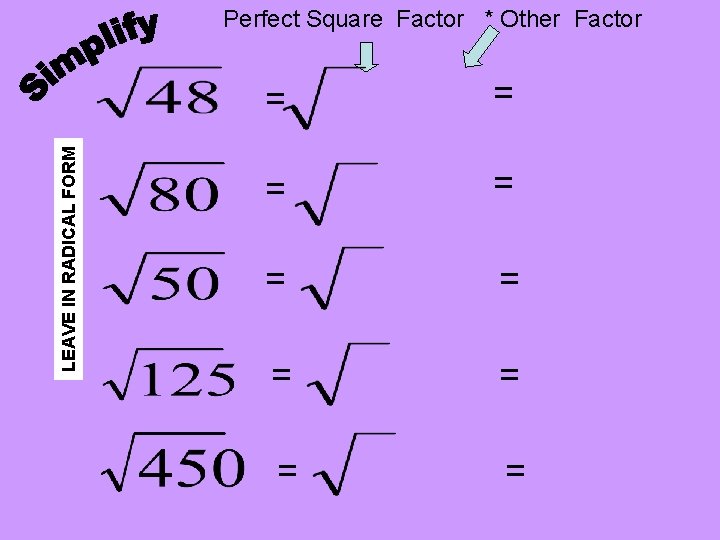
LEAVE IN RADICAL FORM Perfect Square Factor * Other Factor = = = = =
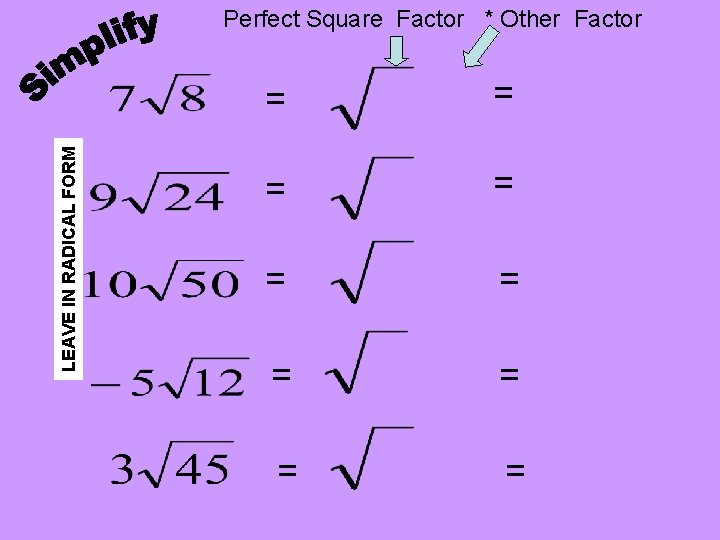
LEAVE IN RADICAL FORM Perfect Square Factor * Other Factor = = = = =
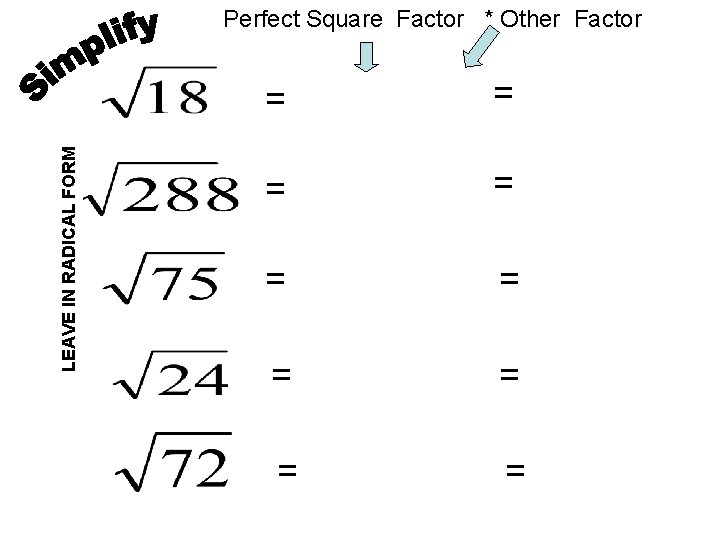
LEAVE IN RADICAL FORM Perfect Square Factor * Other Factor = = = = =

+ To combine radicals: combine the coefficients of like radicals

Simplify each expression
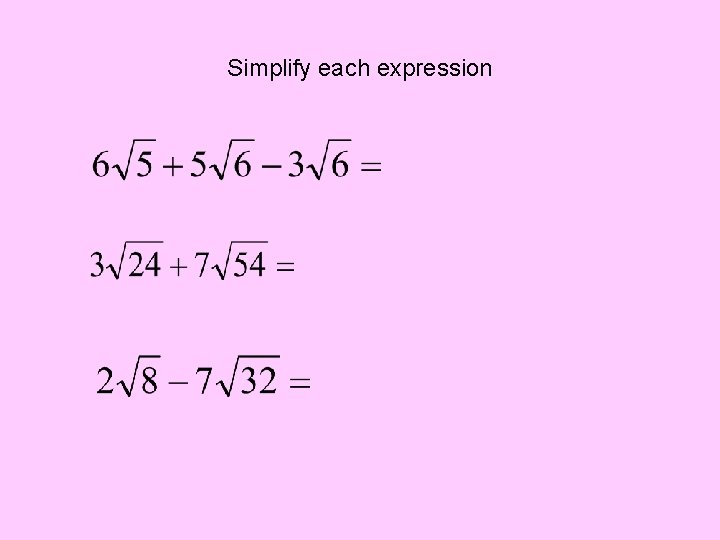
Simplify each expression
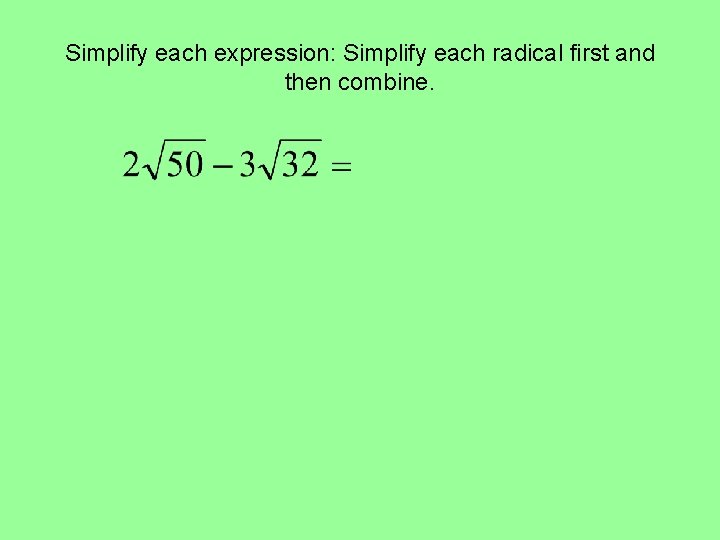
Simplify each expression: Simplify each radical first and then combine.

Simplify each expression: Simplify each radical first and then combine.

LEAVE IN RADICAL FORM Perfect Square Factor * Other Factor = = = = =
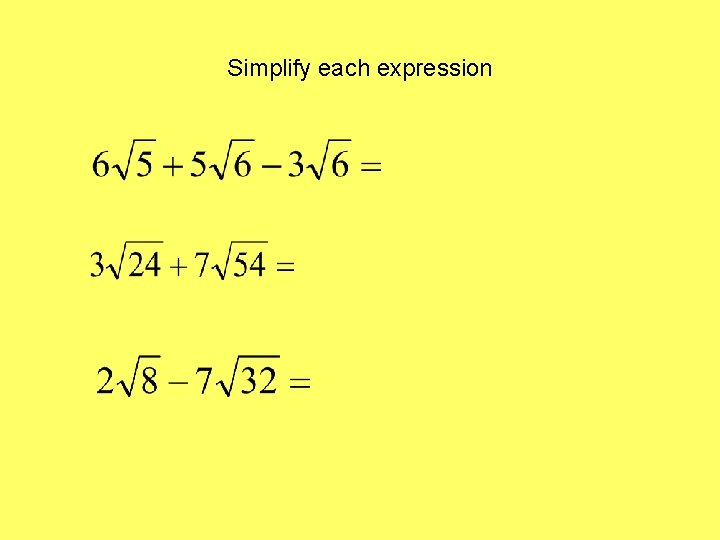
Simplify each expression
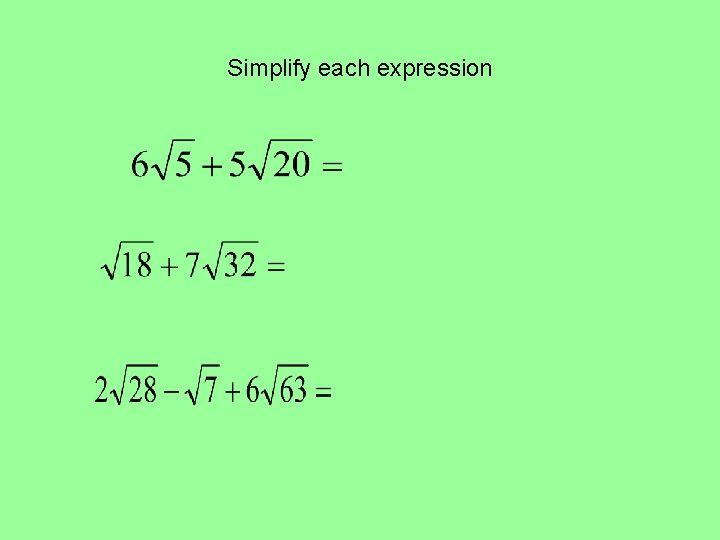
Simplify each expression

WORKSHEET 3)
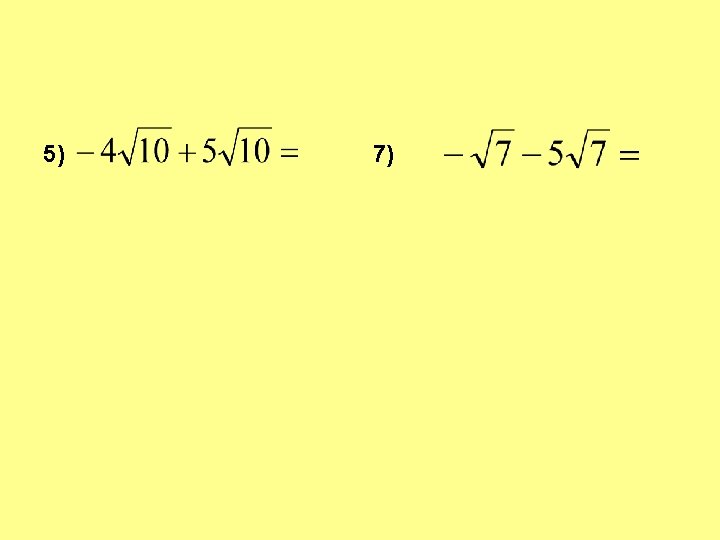
5) 7)

9)
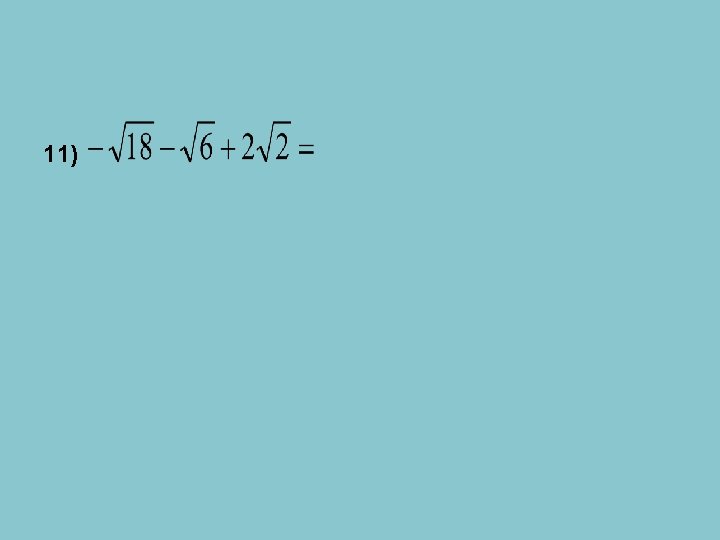
11)
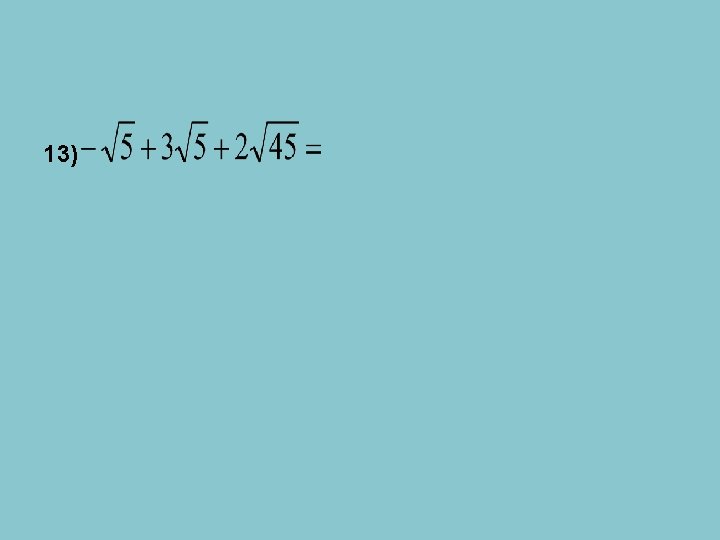
13)
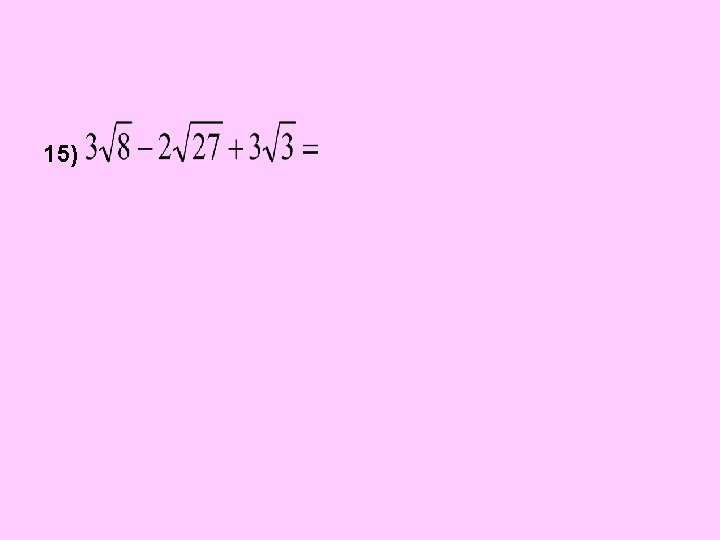
15)
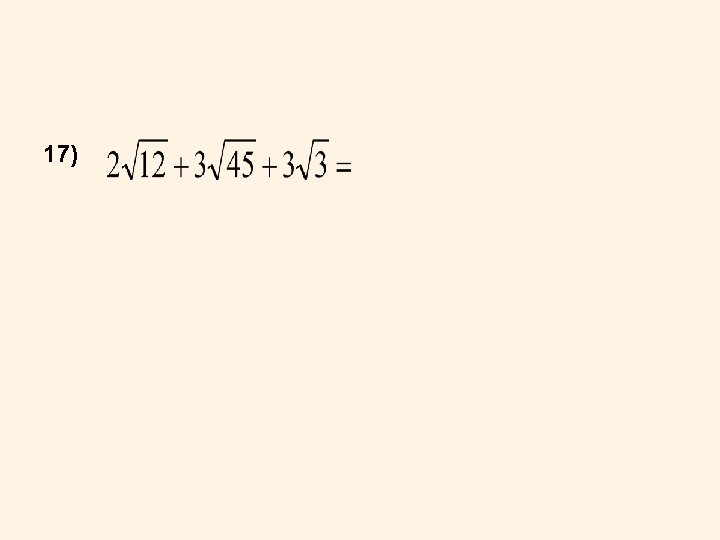
17)



* To multiply radicals: multiply the coefficients and then multiply the radicands and then simplify the remaining radicals.
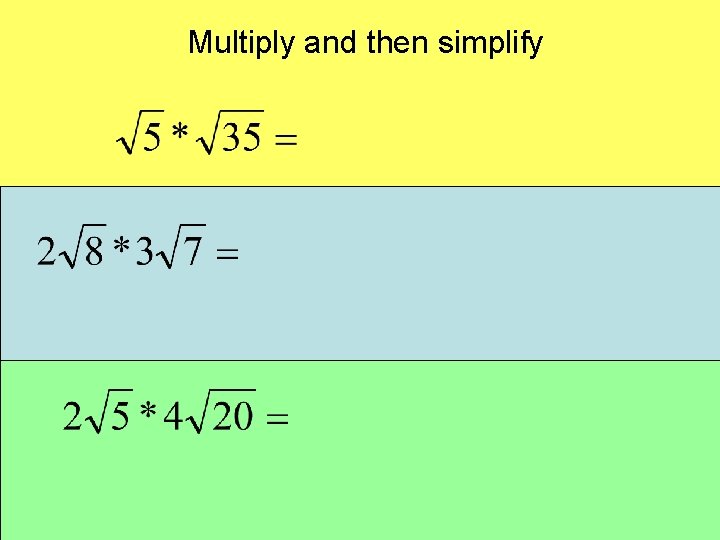
Multiply and then simplify


WORKSHEET(MULT)

WORKSHEET(MULT)

WORKSHEET(MULT)

WORKSHEET(MULT)

WORKSHEET(MULT)

WORKSHEET(MULT)

Using distributive Property • • a(b+c) = ab + ac a(b-c) = ab - ac

USING THE DISTRIBUTIVE PROPERTY

USING THE DISTRIBUTIVE PROPERTY

USING THE DISTRIBUTIVE PROPERTY

USING THE DISTRIBUTIVE PROPERTY

USING THE DISTRIBUTIVE PROPERTY

Using the FOIL

Using the FOIL

Using the FOIL

To divide radicals: divide the coefficients, divide the radicands if possible, and rationalize the denominator so that no radical remains in the denominator
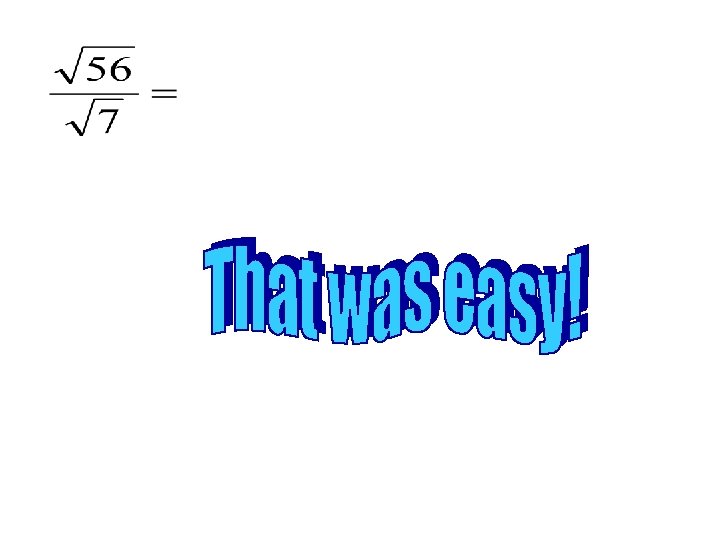

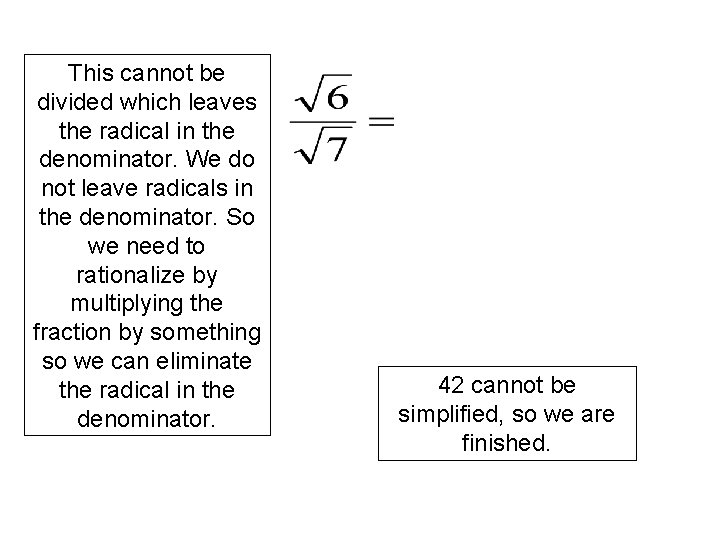
This cannot be divided which leaves the radical in the denominator. We do not leave radicals in the denominator. So we need to rationalize by multiplying the fraction by something so we can eliminate the radical in the denominator. 42 cannot be simplified, so we are finished.

This can be divided which leaves the radical in the denominator. We do not leave radicals in the denominator. So we need to rationalize by multiplying the fraction by something so we can eliminate the radical in the denominator.

This cannot be divided which leaves the radical in the denominator. We do not leave radicals in the denominator. So we need to rationalize by multiplying the fraction by something so we can eliminate the radical in the denominator.
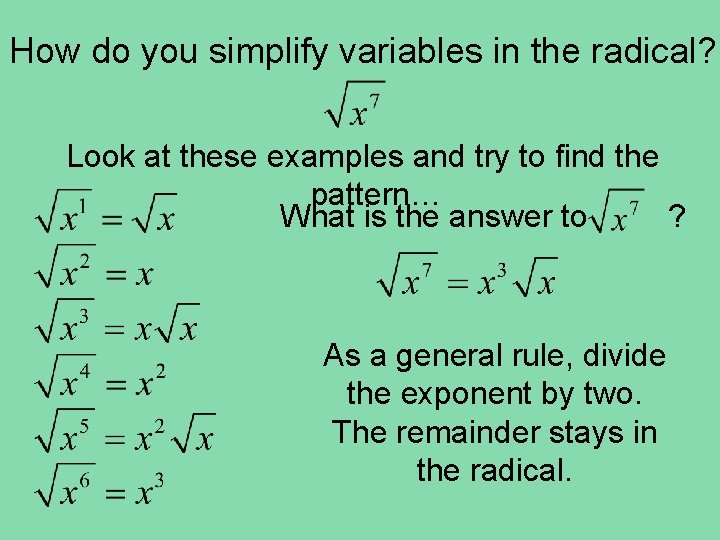
How do you simplify variables in the radical? Look at these examples and try to find the pattern… What is the answer to ? As a general rule, divide the exponent by two. The remainder stays in the radical.

How do you simplify variables in the radical? Look at these examples and try to find the pattern… As a general rule, divide the exponent by two.