Simplifying Multiplying and Dividing Rational Expressions Remember that

Simplifying

Multiplying and Dividing Rational Expressions Remember that a rational number can be expressed as a quotient of two integers. A rational expression can be expressed as a quotient of two polynomials.

Remember, denominators can not = 0. Now, lets go through the steps to simplify a rational expression.

Step 1: Factor the numerator and the denominator completely looking for common factors. Next

What is the common factor? Step 2: Divide the numerator and denominator by the common factor.

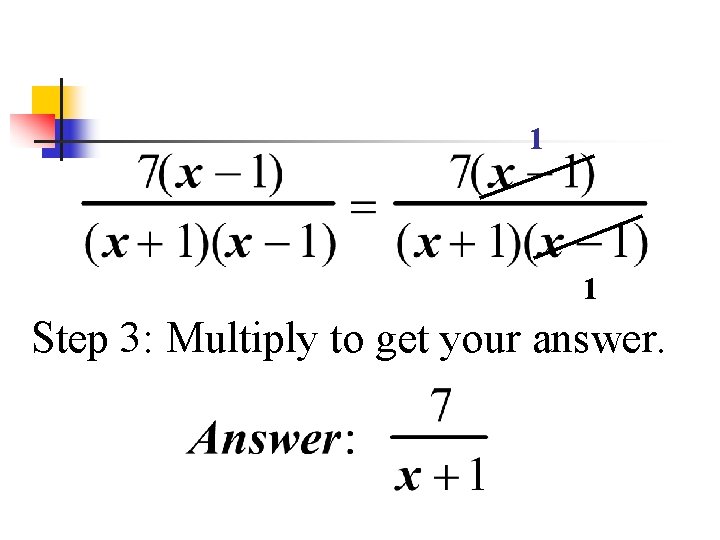
1 1 Step 3: Multiply to get your answer.

Looking at the answer from the previous example, what value of x would make the denominator 0? x= -1 The expression is undefined when the values make the denominator equal to 0

How do I find the values that make an expression undefined? Completely factor the original denominator.

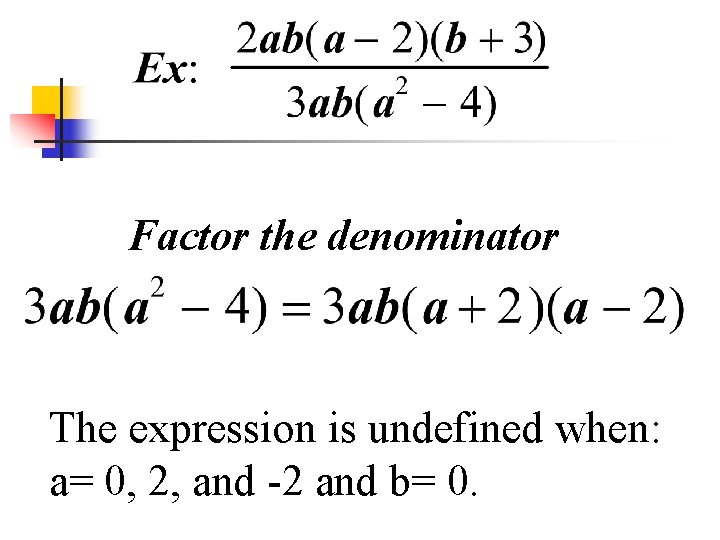
Factor the denominator The expression is undefined when: a= 0, 2, and -2 and b= 0.

Lets go through another example. Factor out the GCF Next

1 1

Now try to do some on your own. Also find the values that make each expression undefined?

Remember how to multiply fractions: First you multiply the numerators then multiply the denominators.

The same method can be used to multiply rational expressions. 1 1 1 1 1

Let’s do another one. Step #1: Factor the numerator and the denominator. Next

Step #2: Divide the numerator and denominator by the common factors. 1 1 1

Step #3: Multiply the numerator and the denominator. Remember how to divide fractions?

Multiply by the reciprocal of the divisor. 1 5 1 4

Dividing rational expressions uses the same procedure. Ex: Simplify

1 1 Next

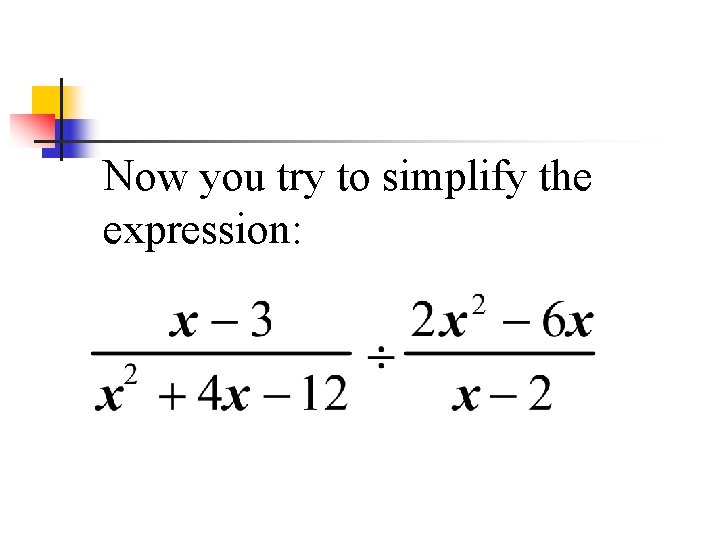
Now you try to simplify the expression:

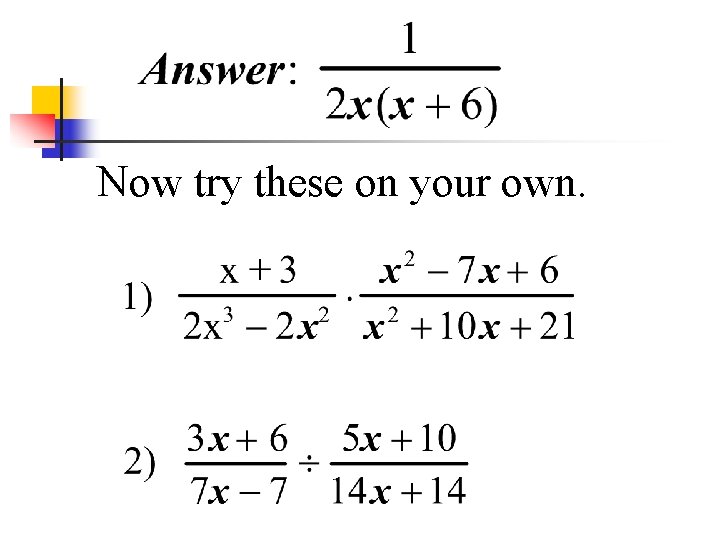
Now try these on your own.

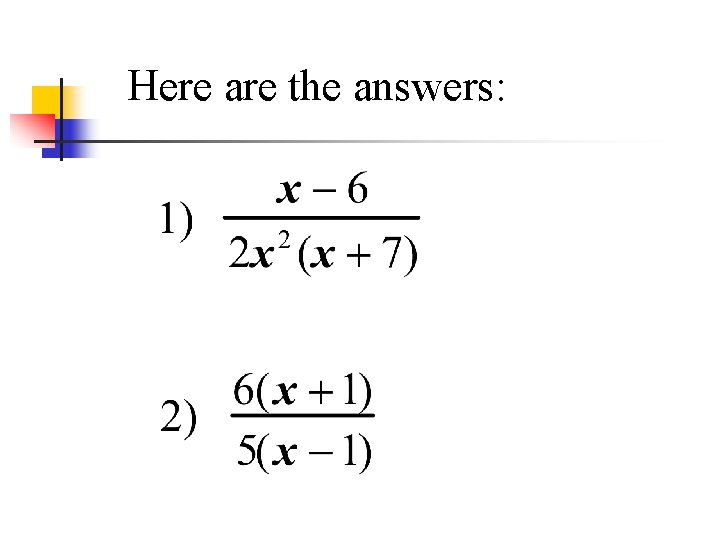
Here are the answers: