Simplifying Algebraic Expressions 7 2 Parts of Algebraic

Simplifying Algebraic Expressions 7. 2

Parts of Algebraic Expressions • Term: Separated by addition and subtraction signs. Example: List the Terms: 3 x+4 y -5 3 x, 4 y, -5

Parts of Algebraic Expressions • Coefficient: The numerical part of a term that contains a variable. Example: Identify the Coefficients: 3 x+4 y -5 3, 4

Parts of Algebraic Expressions • Like Term: Terms that contain the same variable Example: Identify the Like Terms: 3 x +7 +x+2 xy The 3 x and x are like terms

Parts of Algebraic Expressions • Constant A term without a variable Example: Identify the Constant: 5 y +3 +2 x 3

Identify the terms, like terms, coefficients, and constants in 2 x+3 x+4 -4 x • Terms: 2 x, 3 x, 4, -4 x • Like Terms 2 x, 3 x, -4 x • Coefficients: 2, 3, -4 • Constants: 4

Simplify Algebraic Expressions An Algebraic Expression is in its simplest terms when it has: • no like terms • No parenthesis

Simplifying the Expression • Use the Distributive Property Example: 3 x +2 x =(3+2) x =5 x

Ex: Simplify and Justify Steps 4 x+6 -3 x =4 x+6+(-3 x) Definition of Subtraction =4 x+ (-3 x) + 6 Commutative Property =(4+-3)x +6 Distributive Property =X+6 simplify

Ex: Simplify and Justify Your Steps 2 m+3 -7 m-4 =2 m +3+(-7 m) +(-4) Definition of Subtraction =2 m+(-7 m)+3+(-4) Commutative Property =(2+-7)m + 3+ (-4) Distributive Property =-5 m+ (-1) or -5 m -1 Simplify

Ex: Simplify and Justify Your Steps 4 a-6 -2(a-1) =4 a+(-6)+(-2)[a+(-1)] Definition of Subtraction =4 a +(-6) +(-2)(a)+(-2)(-1) Distributive Property =4 a +(-6)+(-2 a) +2 Simplify =4 a +(-2 a) +(-6) + 2 Commutative Property =[4+(-2)] a + (-6) +2 Distributive Property =2 a + (-4) or 2 a -4 Simplify

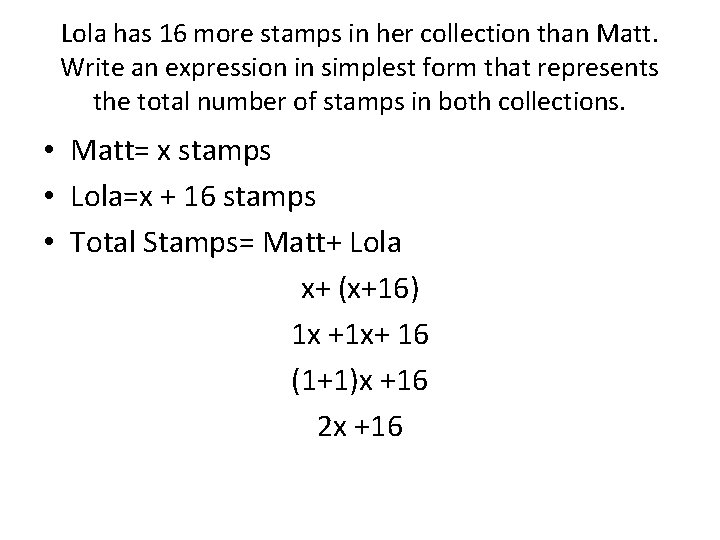
Lola has 16 more stamps in her collection than Matt. Write an expression in simplest form that represents the total number of stamps in both collections. • Matt= x stamps • Lola=x + 16 stamps • Total Stamps= Matt+ Lola x+ (x+16) 1 x +1 x+ 16 (1+1)x +16 2 x +16

Homework Page 302 (16 -44) even