Simplifying Algebraic Expressions 1 5 Vocabulary Term a

* Simplifying Algebraic Expressions 1 -5

Vocabulary Term- a number, a variable, or a product of numbers and variables. Terms in an expression are separated by + and –. Coefficient- is a number that is multiplied by a variable in an algebraic expression.

In the expression 7 x + 9 y + 15, 7 x, 9 y, and 15 are called terms. A term can be a number, a variable, or a product of numbers and variables. Terms in an expression are separated by + and –. 7 x + 5 – 3 y 2 + y + x 3 term In the term 7 x, 7 is called the coefficient. A coefficient is a number that is multiplied by a variable in an algebraic expression. A variable by itself, like y, has a coefficient of 1. So y = 1 y. term Coefficient Variable

Like terms are terms with the same variables raised to the same exponents. The coefficients do not have to be 1 the same. Constants, like 5, , and 3. 2, are also like 2 terms. Like Terms Unlike Terms 3 x and 2 x 5 x 2 and 2 x The exponents are different. w and w 7 6 a and 6 b The variables are different 5 and 1. 8 3. 2 and n Only one term contains a variable

Additional Example 1: Identifying Like Terms Identify like terms in the list. 3 t 5 w 2 7 t 9 v 4 w 2 8 v Look for like variables with like powers. 3 t 5 w 2 7 t Like terms: 3 t and 7 t 9 v 4 w 2 8 v 5 w 2 and 4 w 2 9 v and 8 v Helpful Hint Use different shapes or colors to indicate sets of like terms.

Check It Out: Example 1 On your own. Identify like terms in the list. 2 x 4 y 3 8 x 5 z 5 y 3 8 z

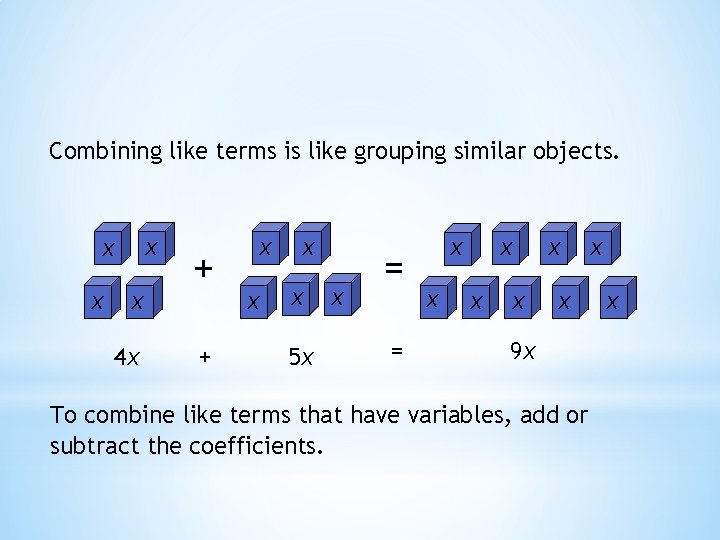
Combining like terms is like grouping similar objects. x x 4 x + + x x 5 x x = = x x x x 9 x To combine like terms that have variables, add or subtract the coefficients. x x

Additional Example 2: Simplifying Algebraic Expressions Simplify. Justify your steps using the Commutative, Associative, and Distributive Properties when necessary. A. 6 t – 4 t 6 t and 4 t are like terms. 2 t Subtract the coefficients. B. 45 x – 37 y + 87 In this expression, there are no like terms to combine.

Additional Example 2: Simplifying Algebraic Expressions Simplify. Justify your steps using the Commutative, Associative, and Distributive Properties when necessary. C. 3 a 2 + 5 b + 11 b 2 – 4 b + 2 a 2 – 6 (3 a 2 + 2 a 2) + (5 b – 4 b) + 11 b 2 – 6 5 a 2 + b + 11 b 2 – 6 Identify like terms. Group like terms. Add or subtract the coefficients.

Check It Out: Example 2 On your own. Simplify. Justify your steps using the Commutative, Associative, and Distributive Properties when necessary. A. 5 y + 3 y B. 2(x 2 – 13 x) + 6

Check It Out: Example 2 On your own. Simplify. Justify your steps using the Commutative, Associative, and Distributive Properties when necessary. C. 4 x 2 + 4 y + 3 x 2 – 4 y + 2 x 2 + 5

Additional Example 3: Geometry Application Write an expression for the perimeter of the triangle. Then simplify the expression. 2 x + 3 3 x + 2 x 2 x + 3 x + 2 + x (x + 3 x + 2 x) + (2 + 3) 6 x + 5 Write an expression using the side lengths. Identify and group like terms. Add the coefficients.

Check It Out: Example 3 On your own. Write an expression for the perimeter of the triangle. Then simplify the expression. 2 x + 1 x