SIMPLIFY EXPRESSIONS WITH INTEGER EXPONENTS PRACTICE ALL OF

SIMPLIFY EXPRESSIONS WITH INTEGER EXPONENTS PRACTICE ALL OF THE PROPERTIES OF EXPONENTS

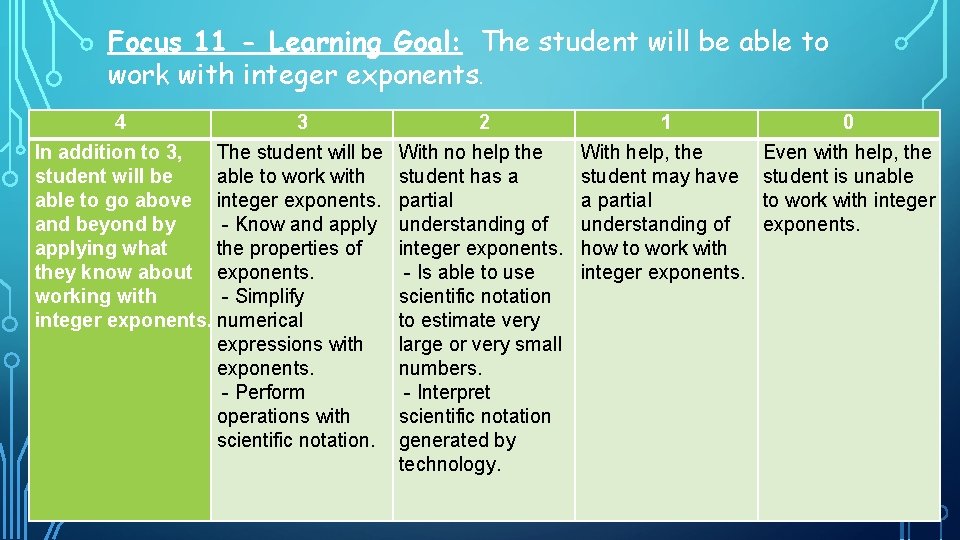
Focus 11 - Learning Goal: The student will be able to work with integer exponents. 4 3 In addition to 3, The student will be able to work with able to go above integer exponents. and beyond by - Know and applying what the properties of they know about exponents. working with - Simplify integer exponents. numerical expressions with exponents. - Perform operations with scientific notation. 2 With no help the student has a partial understanding of integer exponents. - Is able to use scientific notation to estimate very large or very small numbers. - Interpret scientific notation generated by technology. 1 With help, the student may have a partial understanding of how to work with integer exponents. 0 Even with help, the student is unable to work with integer exponents.

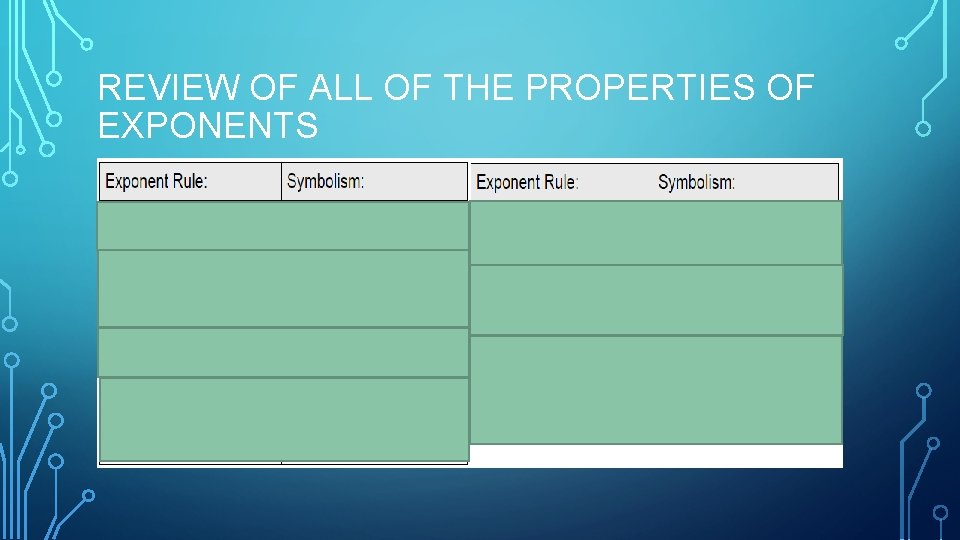
REVIEW OF ALL OF THE PROPERTIES OF EXPONENTS

Practice simplifying expressions with integer exponents using multiple rules. 1. 4 c 0 1. 2. (4)(1) Anything to the zero power is 1. 4 Distribute the Power of 3 to everything in the parenthesis. 3 y 2 (2 y)3 1. = 3 y 2 2. = 3 23 y 5 3. =3 4. = 24 y 5 23 y 3 The “y”s have the same 8 y 5 3. 4 x 2 y 2 xy 2 1. 2 x 2 y xy 2 2. 2 xy y 2 3. 2 x y base, add the exponents. Solve 23. Multiply 3 and 8. Simplify 4 divided by 2. The “x”s have the same base, subtract their exponents: 2 – 1 = 1. Since this is positive, x 1 stays in the numerator. The “y”s have the same base, subtract their exponents: 1 – 2 = -1. Since this is negative, y 1 it moves to the denominator.

Practice simplifying expressions with integer exponents using multiple rules. • 4 Distribute the Power of 4 to EVERY variable in the parenthesis by multiplication. The “x”s have the same base, subtract their exponents: 28 – 8 = 20. Since it is positive, x 20 stays in the numerator. The “y”s have the same base, subtract their exponents: 12 – 4 = 8. Since it is positive, y 8 stays in the numerator.

Practice simplifying expressions with integer exponents using multiple rules. what is in 5. (2 m 3 • 6 m 4)2 Simplify parenthesis. 1. (12 m 7)2 2. 122 m 14 3. 144 m 14 Distribute the Power of 2 to everything in the parenthesis. Solve 122. Select each expression that is equivalent to 1/64. a) 4 -3 b) 8 -2 c) 87 • 8 -9 d) 82 e) 4 -1 • 4 -2