Simplified DES SDES algorithm The SDES encryption algorithm

Simplified DES

S-DES algorithm �The S-DES encryption algorithm takes �an 8 -bit block of plaintext (e. g. , 10111101) � 10 -bit key as input and �produces an 8 -bit block of ciphertext as output. �The S-DES decryption algorithm takes �an 8 -bit block of ciphertext and �the same 10 -bit key used �produce the original 8 -bit block of plaintext.

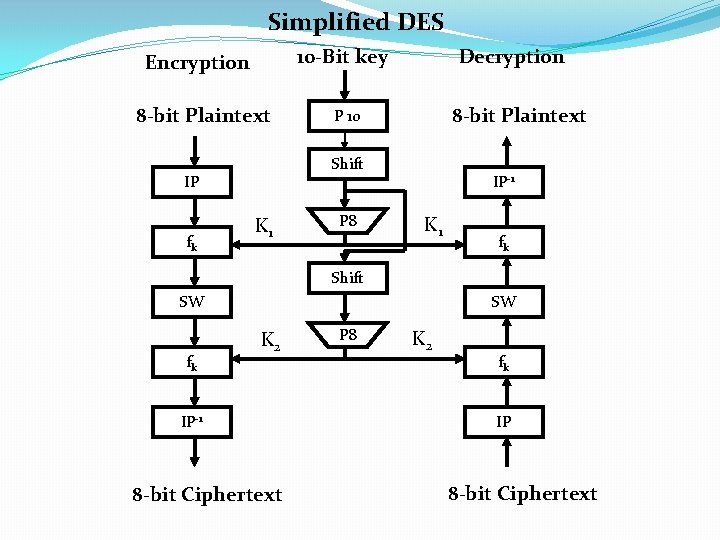
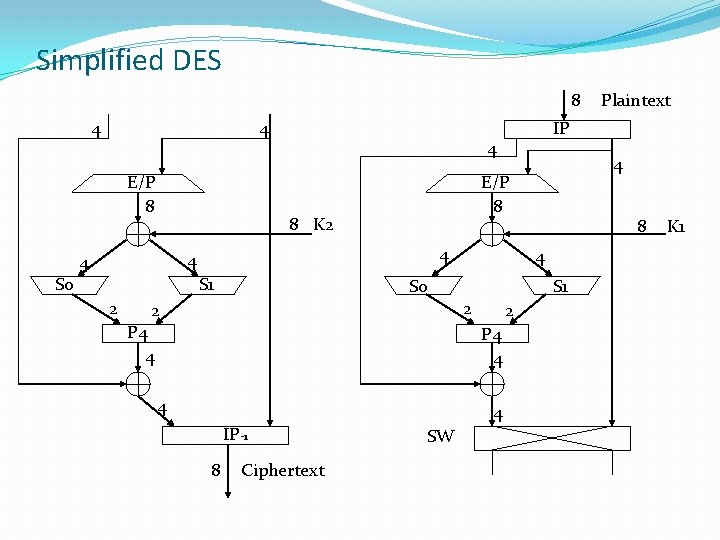
Simplified DES 10 -Bit key Encryption 8 -bit Plaintext P 10 Shift IP fk Decryption K 1 P 8 IP-1 K 1 fk Shift SW fk SW K 2 IP-1 8 -bit Ciphertext P 8 K 2 fk IP 8 -bit Ciphertext

S-DES encryption The encryption algorithm involves five functions: 1. an initial permutation (IP); 2. a complex function labeled fk, which involves both permutation and substitution operations and depends on a key input; 3. a simple permutation function that switches (SW) the two halves of the data; 4. The function fk again; and 5. a permutation function that is the inverse of the initial permutation (IP-1).

The encryption algorithm as a composition of functions Decryption is essentially the reverse of encryption

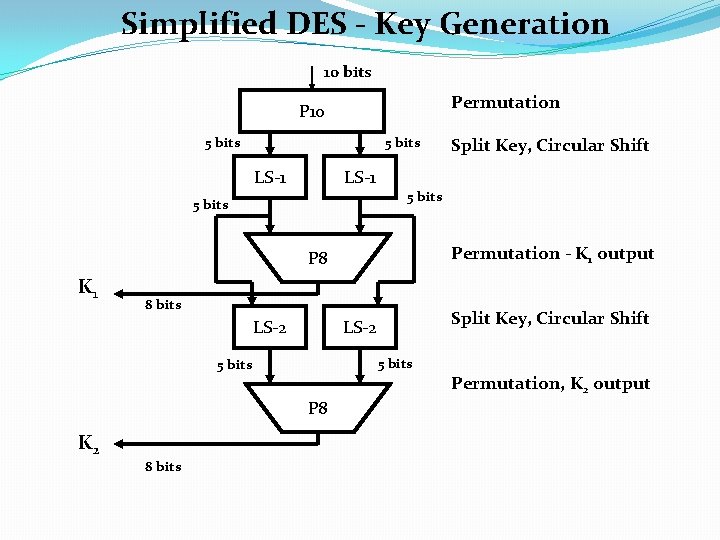
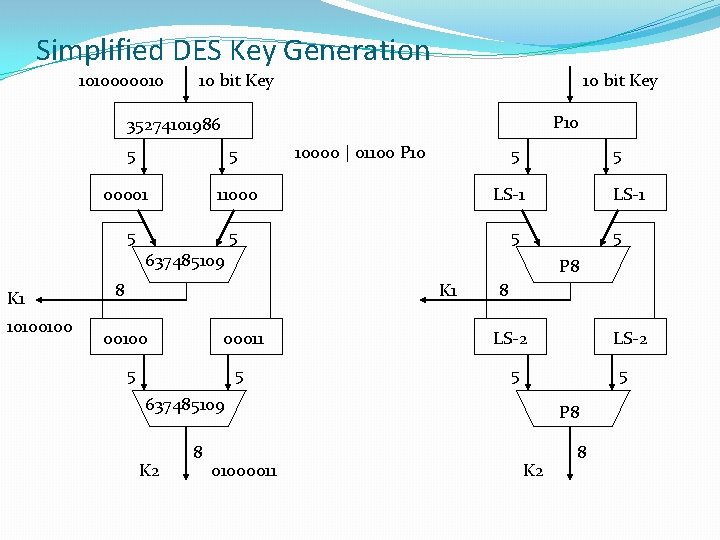
Simplified DES - Key Generation 10 bits Permutation P 10 5 bits LS-1 5 bits Permutation - K 1 output P 8 K 1 8 bits LS-2 5 bits P 8 K 2 8 bits Split Key, Circular Shift LS-2 5 bits Split Key, Circular Shift Permutation, K 2 output

S-DES Key Generation �S-DES depends on the use of a 10 -bit key shared between sender and receiver. �Two 8 -bit subkeys are produced for use in particular stages of the encryption and decryption algorithm.

Simplified DES - Key Generation P 10 Permutation: P 10(in-order) = k 1, k 2, k 3, k 4, k 5, k 6, k 7, k 8, k 9, k 10 (1010000010) P 10(out-order)= k 3, k 5, k 2, k 7, k 4, k 10, k 1, k 9, k 8, k 6 (1000001100) Split the permuted key into 2 five-bit halves and circular left shift 1 Input = 10000 01100 Output = 00001 11000 P 8 Permutation - selects and permutes 8 of the 10 bits P 8 6 3 7 4 Result is Sub-key K 1 = 10100100 8 5 10 9

Simplified DES - Key Generation To get sub-key K 2: Take output of original circular left shift 1 and shift an additional 2 Input = 00001 11000 Output = 00100 00011 Apply P 8 to this value to produce K 2 = 01000011 This completes the generation of K 1 and K 2

Simplified DES - Encryption Ø Two permutation functions (initial - IP, and final IP-1), where IP-1 is the inverse of IP; that is IP-1(IP(X)) = X. Ø Two permutation/substitution functions fk each using one sub-key, on the left (L) and right (R) data elements. That is: fk(L, R) = (L F(R, SK), R) where SK is a sub-key and is the bit-by-bit Exclusive OR. Ø One switch function SW that interchanges the left and right 4 bits so the second instance of fk operates on a different set of bits.

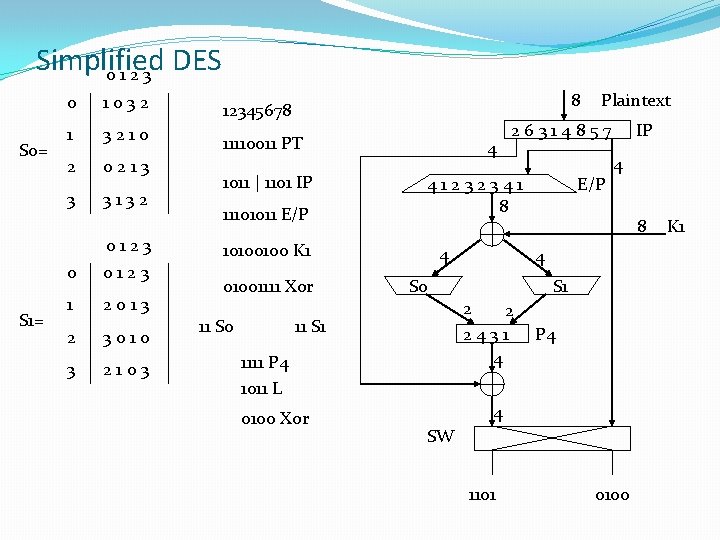
Simplified DES - Initial & Final Permutation IP IP 2 6 3 1 4 8 5 7 7 2 8 6 Input = 01001101 Output = 11000110 IP-1 4 1 3 Input = 11000110 Output = 01001101 Result is IP-1(IP(X)) = X 5

Simplified DES - Function fk Assume output of the IP stage is = 10111101 Then L, R = 1011, 1101 And fk(L, R) = (L F(R, SK), R) So fk(1011, 1101) = (1011 F(R, SK), 1101) Now assume F(R, SK) = F(1101, SK) for some sub-key = 1110 (this value will change depending on the sub-key). Then: fk(1011, 1101) = (1011 1110, 1101) = 0101, 1101 Next we need to describe the complex function F(R, SK).

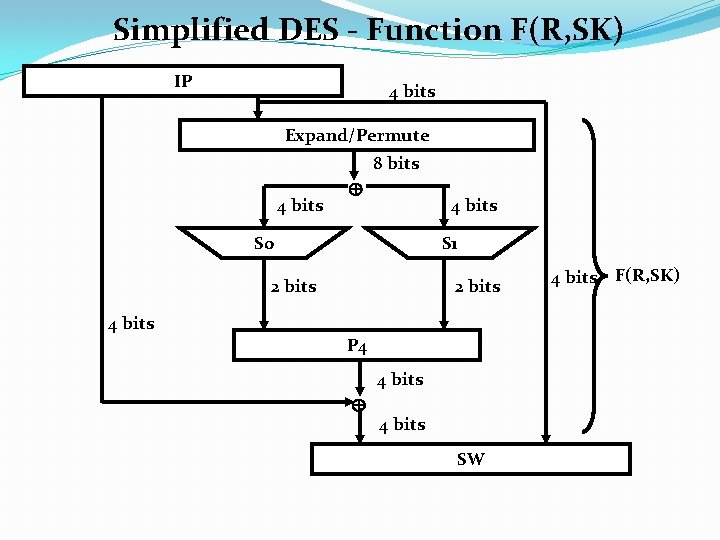
Simplified DES - Function F(R, SK) IP 4 bits Expand/Permute 8 bits 4 bits S 0 S 1 2 bits 4 bits 2 bits P 4 4 bits SW 4 bits F(R, SK)

Simplified DES - Function Parts of F(R, SK) Expansion/Permutation (4 bits n 1, n 2, n 3, n 4) to 8 bits E/P 4 1 2 3 4 1 Arrange these bits as follows: n 4 | n 1 , n 2 | n 3 (left half of expansion/permutation) n 2 | n 3 , n 4 | n 1 (right half) Compute: n 4 k 11 | n 1 k 12 , n 2 k 13 | n 3 k 14 n 2 k 15 | n 3 k 16 , n 4 k 17 | n 1 k 18

Simplified DES - Function Parts of F(R, SK) Rename these 8 bits: Row 1 Row 2 p 0, 0 | p 0, 1 p 0, 2 | p 0, 3 p 1, 0 | p 1, 1 p 1, 2 | p 1, 3 The first 4 bits, row 1 are input to the s-box S 0, 2 nd row to S-box S 1 to produce a 2 -bit output for each input bit as follows; S 0 0 1 2 3 1 0 3 2 1 0 0 2 1 3 3 1 3 2 For example, S 0, p 0, 0 = 01; S 1, p 1, 1 = 00 S 1 0 1 2 3 2 0 1 3 3 0 1 0 2 1 0 3

Simplified DES - Function Parts of F(R, SK) P 4 Permutation: 2 bit input from S 0, 2 bits from S 1 P 4 2 4 3 1 P 4 output = output of fk Switch function: interchanges the left and right halves so the second instance of fk using the second key operates on different data. The second instance of fk operates the same as described above using the k 2 sub-key and the switched input. Decryption uses all the same functions run backwards.

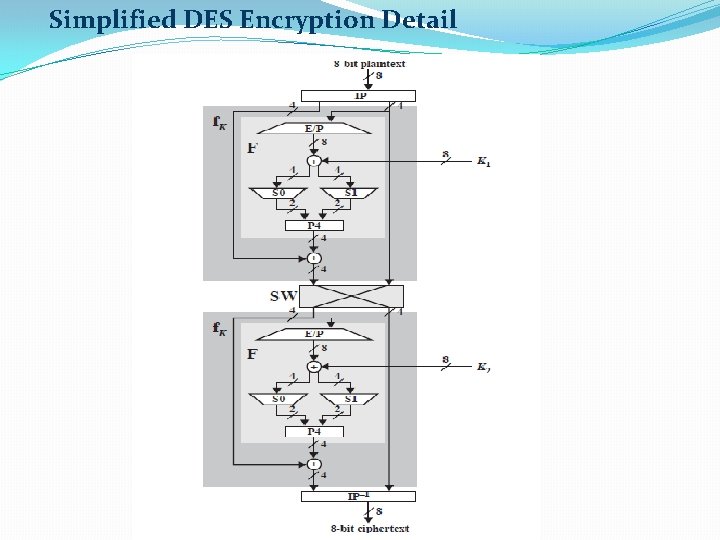
Simplified DES Encryption Detail

Simplified DES Key Generation 1010000010 10 bit Key P 10 35274101986 5 5 00001 10000 | 01100 P 10 5 11000 5 5 LS-1 5 5 5 637485109 K 1 10100100 P 8 8 K 1 00100 8 00011 LS-2 5 5 5 K 2 01000011 LS-2 5 637485109 8 LS-1 P 8 K 2 8

Simplified DES 8 4 4 E/P 8 S 0 4 S 1 2 2 P 4 4 4 4 8 Ciphertext SW 8 4 S 0 IP-1 4 E/P 8 4 4 IP 4 8 K 2 Plaintext K 1

Simplified DES 0123 S 0= 0 1032 1 3210 2 0213 3 3132 0123 S 1= 0 0123 1 2013 2 3010 3 2103 8 12345678 11110011 PT 1011 | 1101 IP 11101011 E/P 4 01001111 Xor 11 S 0 4 4 8 S 1 2 2 2431 4 1111 P 4 1011 L E/P IP 4 S 0 11 S 1 0100 Xor 26314857 41232341 8 10100100 K 1 Plaintext P 4 4 SW 1101 0100 K 1

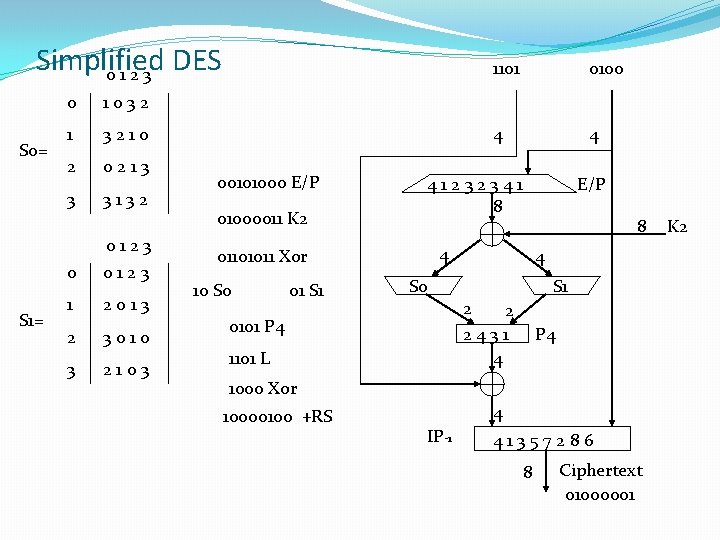
Simplified DES 0123 S 0= 0 1032 1 3210 2 0213 3 3132 0123 S 1= 0 0123 1 2013 2 3010 3 2103 00101000 E/P 01000011 K 2 01 S 1 0100 4 4 41232341 8 E/P 8 4 01101011 Xor 10 S 0 1101 4 S 0 S 1 2 2 2431 4 0101 P 4 1101 L P 4 1000 Xor 10000100 +RS 4 IP-1 41357286 8 Ciphertext 01000001 K 2