Simple Switching Transients o o Considering AC Drives

Simple Switching Transients o o Considering AC Drives Two Switching Cases: 1 - Closing a CCT Breaker, Energizing Load 2 - Opening a Breaker, Clearing Fault

The CCT Closing Transients Energizing an RL CCT load: Series R and L 1 -Source Imp. neglig. 2 -source: V, f=50, 60 Hz o P. F. =

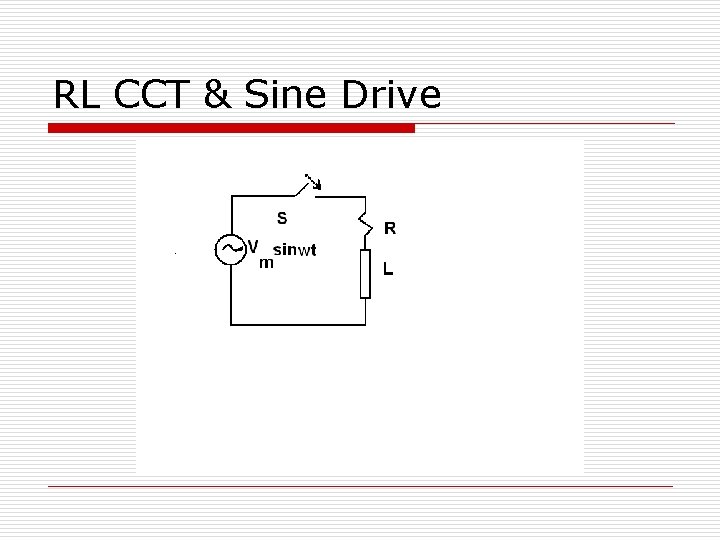
RL CCT & Sine Drive

CCT. B. Closes o Related O. D. E RI + L d. I/dt=V=

Rewriting i(s) o If: A=(Vm/L). ω. Cosθ B=(Vm/L). sinθ α=R/L

Necessary Inverse Transforms

Time Response After Reformulation o Noting: tanΦ=ωL/R=ω/α

Discussion on Response (RL Load) o Two Components in Response: 1 - The steady state (sin. Osc. Term) 2 - The Transient (exp. Term) If θ=Φ : Transient term=0 I(t) sym. If θ-Φ=±∏/2 : peak = 2 x (s. s. comp. ) I(t) Max. Asym.

Breaker Capability (conclusion 1) CCT. B. May Close into a S. C. (i. e. R, L relavent to source) θ: Arbitrary In 3 ph a good chance of Full Asym. □ Designed Elec. , Mech, & Thermally to withstand this duty □ Perform Subsequent open & Reclose o

Serious Forces (conclusion 2) Buckling of parts can occur by Electro. Forces caused by current □Very high current, weld the contacts □If contact popping happens conditions get worse □Any weld formed must not impair the efficiency of CCT B. □Mechanism be able to break weld and rupture the fault current o

Breaking Current o (conclusion 3) time from Fa. initiation to contacts parting, & instant. Current: --Actual current to interrupt --C. B. of high decr. , duty is less severe □Damage, Thermal O. L. lines, system stability Fast. Opening of S. C.

Considering Transient & Sub. Transient reactances conclusion 4 o o S. C. close to Generator T. & Sub. T. reactance Extra high first peak of Is. c. After T. & sub. T. , for several periods (1 Ph. fault): current zero is lacking

Example : 3 ph Cap. Bs. 1 st: 3 X 60 MVA, 13. 8 KV, star con. 2 nd: 3 X 30 MVA, 13. 8 KV, star con. ●Be paralleled momen. by 100Ω s. steel ●Design resistors: i. e. : length, cross section ●Require: R’s Temp. rise<200 C sw. op. when one Bank. in pos. peak, other in neg. peak o

Stainless steel characteristics density: 7. 9 g/ cubic. cm o S. Heat: 0. 5 J/g per C o Resistivity: 72μΩcm Note: no heat is lost during Sw. Op. o ●What is weight of resistor ●What will be the peak current

Example Solution o o o R=ρ l/s=R/ρ=100/(72 x 10^(-8))= 1. 389 x 10^8 Reactance cap. Bank 1: (13. 8)^2/160=1. 058 Ω C 1=1/(1. 058 x 314. 15)=3. 0 m. F C 2=1. 5 m. F Peak voltage: 13. 8 X√ 2/√ 3=11. 27 KV Dissipated E. : 1/2 Ceqx(V 1(0)-V 2(0))^2 = 2. 54 x 10^5 joules Ceq=C 1 C 2/(C 1+C 2)

Solution ……continued Dissip. Energy. =v. g. k. ∆T= =lxsx 7. 9 x 0. 5 x 200=790 xlxs o ls=2. 54 x 10^5/790=321. 52 o l/sxls=l^2=1. 389 x 10^8 x 321. 52= =21. 13 x 10^2 sq. m. l=45. 96 m S=321. 5/4596=6. 99 x 10^-2 sq. cm. m=lsg=321. 52 x 7. 9=2. 54 Kg I(peak)=∆V/R=22. 54 x 10^3/100=225. 4 A o

Simple Sw. : Cap. Inrush current o Shunt Capacitors : closing op. Assume a number of parallel units In Fig. there are two with sw: S 1, S 2 o Source Inductance L, local CCT L 1 o I(t)=V(0)/Z 0 sinω0 t o Z 0=√L/C, V(0): inst. Voltage o ω0=1/√LC o o

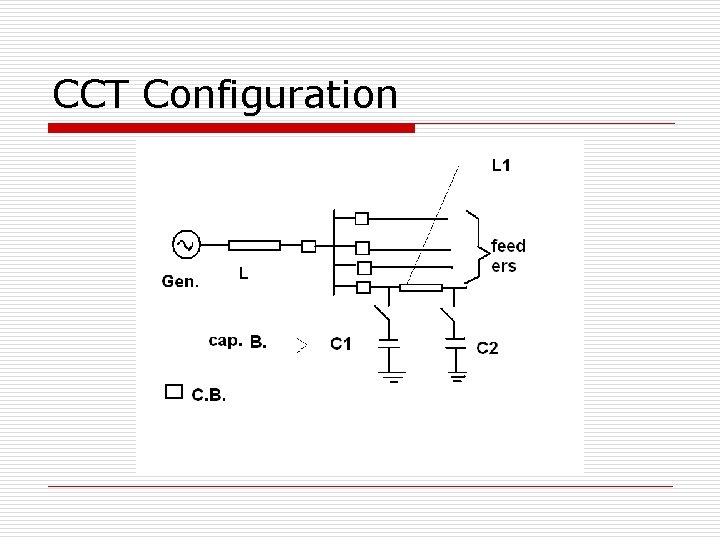
CCT Configuration

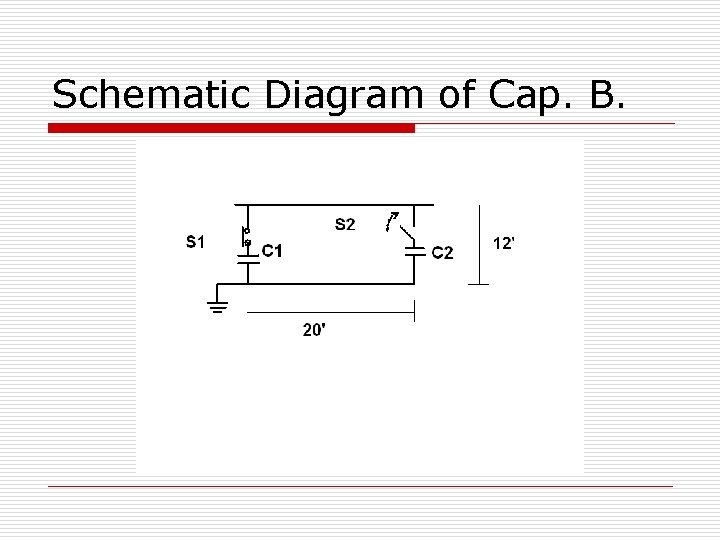
Consider 34. 5 KV (a S. Gr. ) system S. C. current at Bus: 25 KA (rms), sym o If C 1=18 MVA, C 2=10 MVA o Next Fig: Bus B. Schematic diag. (dimen. ) CALCULATION RESULTS(1 st Trans. S 1 close): o I=1. 8 x 10^7/(√ 3 x 34. 5 x 10^3)=301. 2 A o Xc 1=34500/(√ 3 x 301. 2)=66. 13Ω o C 1=40. 1 μF o Xs=34. 5/(√ 3 x 25)=0. 797Ω , L=0. 0021 H o Ip=(34. 5√ 2/√ 3)(40. 1/2100)^0. 5=3. 893 KA o f=1/2∏√LC 1=548 Hz o

Schematic Diagram of Cap. B.

Closing Switch S 2 o o o o (2 nd Transient) L 1 depends geometry & Physical Dim. Inductance of Bus work prop: Cond. size Al. angles & channels used in Cap. Banks Ind. Param. : 0. 2 to 0. 4 μH/ft(0. 3 selected) L 1=0. 3 X 64(ft)=19. 2 μH C 2=22. 28 μF C 1 C 2/(C 1+C 2)=14. 32μF

2 nd Transient Results o Z 01=√(19. 2/14. 32)=1. 158Ω Inrush from C 1 to C 2(C 2 discharged, C 1 Peak) Iinr=Vp/Z 01=(34. 5√ 2)/(√ 3 x 1. 158)=22. 33 KA o Freqinr=10^6/2∏(√ 19. 2 x 14. 32) =9. 6 KHz o Justifies negl. the o o o Current from Source Extreme Case (Vc 2=-Vp), results: Iinr. =48 KA

Discussion of H. F. Inrush Eff. s o o o Severe Mechanical Stresses Transients in Nearby CCTs Cap. Bank Inrush Reduction Methods: Z increase, Extra L in form of Reactor Add R, damp Osc. s (and short it later) the 2 nd switch cost much Synchronous Sw. (pre-strike limited app. )

3 rd stage: Final Common Voltage of 2 nd: C 1 V 1(0)+C 2 V 2(0)=(C 1+C 2). V(final) i. e. : Vfinal=(C 1 V 1(0)+C 2 V 2(0))/(C 1+C 2)= (40. 1 x 28. 17 -22. 28 x 8)/(40. 1+22. 28)=15. 25 KV o Now two cap. s swing to sys. Peak o Osc. Freq. = 1/[2∏√L(C 1+C 2)]=439. 7 Hz o V, rises: 28. 17+(28. 17 -15. 25)=41. 09 KV o Current (Vp-Vf)√[(C 1+C 2)/L]. sinω1 t= (28. 17 -15. 25)√(62. 38/2100). Sinω1 t= 2. 227 sinω1 t KA…………Fig. of OSC. o

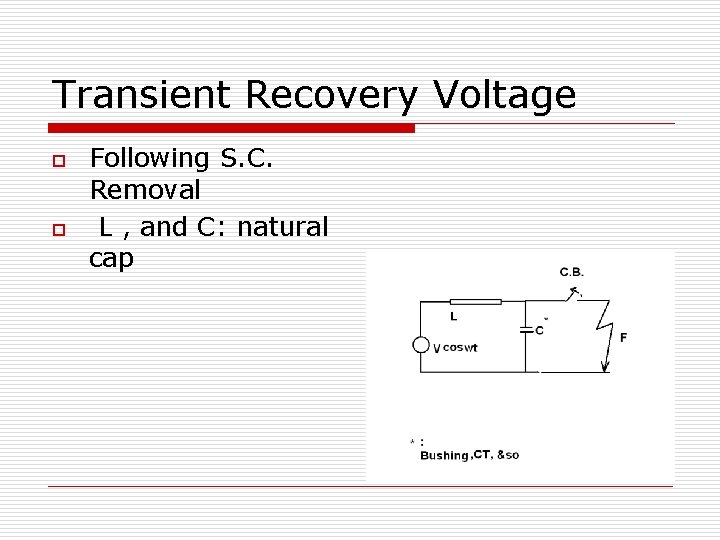
Transient Recovery Voltage o o Following S. C. Removal L , and C: natural cap

Simplifying Assumptions o o o o CCT’s R, and Losses ignored After sep. of contacts, I flows in Arc I reach zero by controlling arc In Ac two I=0 in each cycle Current : Symm. & compl. Inductive At I=0 : Vcc. T Max, VCB=Varc Assuming Varc=0 Time measu. from Inst. of Interr.

CCT Equation o The KVL & Ic: L d. I/dt+ Vc=Vm cosωt I=C d. Vc/dt (only I) o o - Physical Inter. Pr. : Ultimately: V supply t=0, previous arc V=0 C charged, through L & cause Osc.

Similar to LC cc. T analysis o Assuming: ω0=1/LC applying L. T. : o Vc(0)=0 arc vol. o Vc’(0)=I(0)/C=0

Time Respose o Inv. Transf. just 1 st term Need: o Then: o Vc(t) is TRV Eq. : o

TRV Eq. (Park & Skeats) Discussion o As ω0 » ω , o Thus: o ∆V(P. F. ) very small

TRV Discussion Continued o o □ Fig : TRVp=2 x P. F. Vp TRV Osc. s damped out C. B. Ops follows Cap. Being charged VCB rises fast if: - L or C or both very small (ω0 large) if RRRV>RDSB : Reignition □ Then o TRV named “Restriking Voltage” Switch passes If (another half Cycle)

Experimental TRV results o o o The TRV lasts 600 μs Decline of current TRV starts a small opp. polar. To ins. Vol. due to: some “Current Chopping” Shows the H. F. Osc. Shows how H. F. Damped

r. r. r. v. factor o o o o A measure of severity of CCT for C. B. r. r. r. v. s high as Natural freq. higher air-cored reactor L=1 m. H, C=400 p. F F 0=1/(2∏√ 10^-3 x 10^-10)=250 KHz T 0=4μs, in T 0/2 TRV swing to 2 Vp In a 13. 8 KV CCT , r. r. r. v. =2 x 13. 8√ 2/(2 x√ 3)=11. 3 KV/μs Beyond Capab. Most C. B. s Ex. Of very fact TRV: Kilometric Faults ch. 9

Interruption of Asymmetrical If o o o Sw. closes at random, I likely to Asym And Degree of Asym. for If Now C. B. opens at I=0, V not at peak TRV now is not so High : Figure R. V. osc. Around Vinst. (nolonger at Peak) TRV is not as high

TRV considerig C. B. Arc Voltage o If arc vol. not negl. The inv. Transf. of term: o Vc(0)=arc volt. , I=0 o Increasing Sw. Trans. o o Effect: I more into Phase with supply voltage Fig.

Assignment No. 1 o Question 1 o C 1, 120 KV o o o 1 st S closed 45μs later G What is IR 2? & Vc 1? C 1=5μF, C 2=0. 5μF R 1=100Ω, R 2=1000Ω

Solution of Question 1 o o o C 1 V 1(0)+C 2 V 2(0)=(C 1+C 2)Vfinal=C 1/(C 1+C 2). V 1(0)=600/5. 5= 109. KV With τ=100 x 0. 4545=45. 45μs V 2(t)=109. (1 -e^(-t/45. 45))=68. KV Therefore IR 2=68 KV/1000=68 A V 1(t)=120 -11(1 -e^(-t/45. 45))=113. KV

Question 2 o C 1 has 1. 0 C, C 2 o C 1=60, C 2=40μF o o discharged R=5 Ω Ipeak? o I(t=200μs) ? Eultimate in C 2 ? o Vc 1(ultimate) ? o

Solution of Question 2 o o o Ipeak=1 x 10^6/60/5=3. 33 KA Ceq=24μF, τ=5 x 24=120μs I(t=200μs)=3. 33 xe^(-t/120)=629. 5 A Vfinal=1 x 10^6/(60+40)=10 KV 1/2 x 40 x 10^-6 x(10^8)=2000 Js

Question 3 o Field coil of a machine, S 1 closes 1 s, Energy in coil? Energy dissipated? S. S. reached, S 1 opened S 2 o 0. 1 s. later o o o closed Vs 1? E dissipated in R 2 ? L=2 H, R 1=3. 6Ω R 2=10Ω

Soultion (Question 3) o o o o o Ifinal=800/3. 6=222. 22 A I(t=1)=222. 2 x(1 -e^(-R 1 t/L))=185. 5 A 1/2 LI^2=34406. Js Esuppl. =∫VI dt=800^2/3. 6∫(1 -e^(-1. 8 t))dt =1. 778 x 10^5[t+e^(-1. 8 t)/1. 8]= =95338 Js Edissip. =95338 -34406=60932 Js IR 2(t=0. 1 s)=222. 2 xe^(-13. 6 t/2)=112. 6 A VR 2=1126 volts, Vs 1=800+1126=1926 volts Es. s. =1/2*2*222. 2^2=49380 Js, ER 2=49380 X 10/13. 6=36310 Js

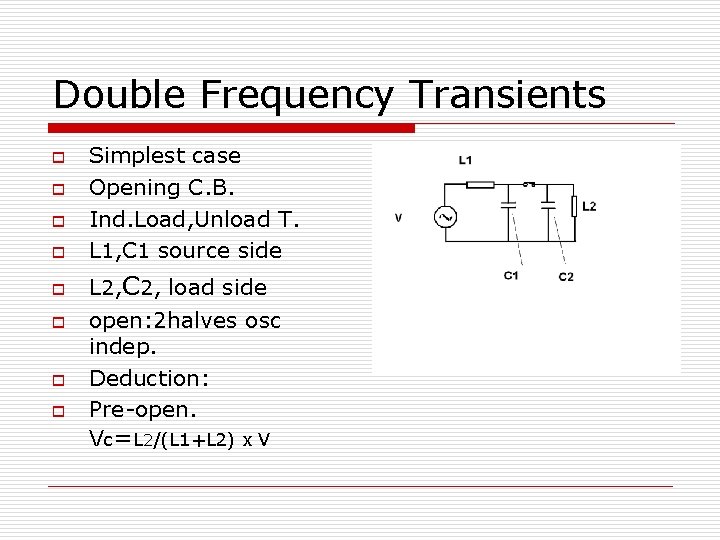
Double Frequency Transients o o o o Simplest case Opening C. B. Ind. Load, Unload T. L 1, C 1 source side L 2, C 2, load side open: 2 halves osc indep. Deduction: Pre-open. Vc=L 2/(L 1+L 2) x V

D. F. Transients continued o Normally L 2» L 1 o C 1 & C 2 charged to about V(t) of Sys. o This V, at peak when I=0 o C 2 discharge via L 2, f 2=1/(2∏√(L 2. C 2)) o o C 1 osc f 1=1/(2∏√L 1. C 1)) about Vsys Figures : Load side Tran. s & Source side Transients

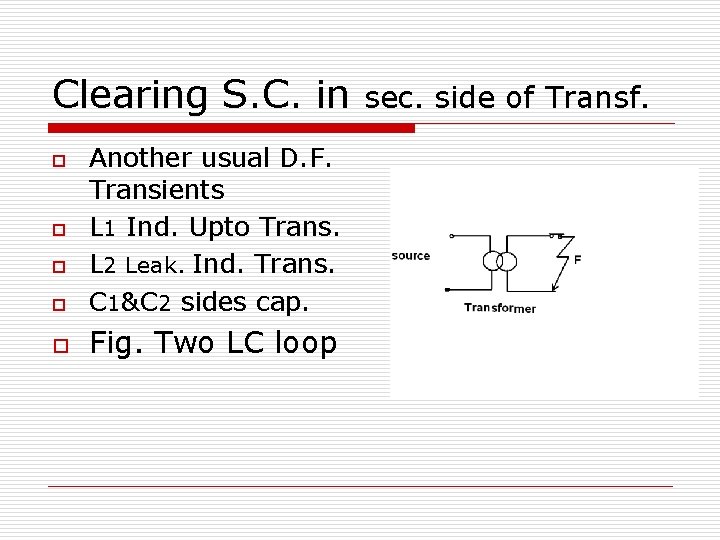
Clearing S. C. in o Another usual D. F. Transients L 1 Ind. Upto Trans. L 2 Leak. Ind. Trans. C 1&C 2 sides cap. o Fig. Two LC loop o o o sec. side of Transf.

Second D. F. Transients o Eq. CCT. o Vc 1(0)=L 2/(L 1+L 2). V o o o Vc 1=V-L 1 d. I 1/dt= Vc 1(0)+1/C 1∫(I 1 -I 2)dt Vc 2=1/C 2∫I 2. dt Vc 2=V-L 1 d. I 1/dt. L 2 d. I 2/dt

Apply the L. T. to solve Eq. s o o V/s-L 1 si 1(s)L 1 I 1(0)=Vc 1(0)/s+1/C 1 s[i 1(s)-i 2(s)] -i 1(s)(L 1 s+1/C 1 s)+i 2(s)/C 1(s)= Vc 1(0)/s+L 1 I 1(0)-L 2. si 2(s)+L 2 I 2(0) o Vc 2(s)=i 2(s)/s. C 2 o Vc 2(s)=V/s-L 1 si 1(s)+L 1 I 1(0)L 2 si 2(s)+L 2 I 2(0)