Simple Stochastic Games Mean Payoff Games Parity Games

Simple Stochastic Games Mean Payoff Games Parity Games Uri Zwick Tel Aviv University

Simple Stochastic Games Randomized subexponential algorithm for SSG Mean Payoff Games Parity Games Deterministic subexponential algorithm for PG

Simple Stochastic Games Mean Payoff Games Parity Games

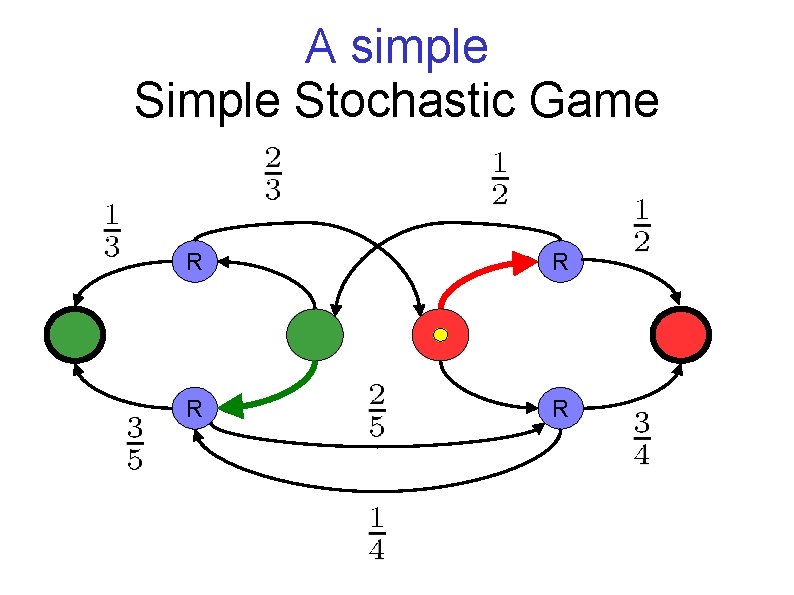
A simple Stochastic Game R R

Simple Stochastic game (SSGs) Reachability version [Condon (1992)] R MAX RAND MAXsink minsink Two Players: MAX and min Objective: MAX/min the probability of getting to the MAX-sink

Simple Stochastic games (SSGs) Strategies A general strategy may be randomized and history dependent A positional strategy is deterministic and history independent Positional strategy for MAX: choice of an outgoing edge from each MAX vertex

Simple Stochastic games (SSGs) Values Every vertex i in the game has a value vi positional general Both players have positional optimal strategies There are strategies that are optimal for every starting position

Simple Stochastic game (SSGs) [Condon (1992)] Terminating binary games The outdegrees of all non-sinks are 2 All probabilities are ½. The game terminates with prob. 1 Easy reduction from general games to terminating binary games

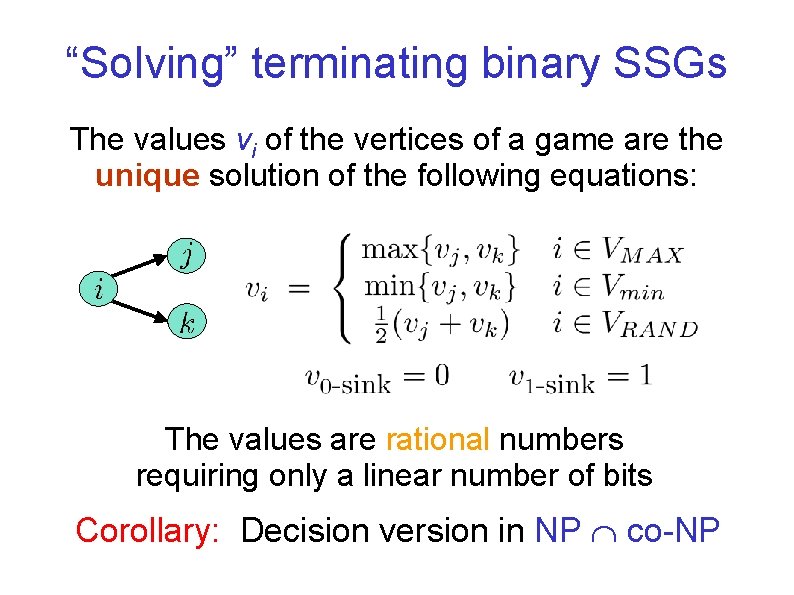
“Solving” terminating binary SSGs The values vi of the vertices of a game are the unique solution of the following equations: The values are rational numbers requiring only a linear number of bits Corollary: Decision version in NP co-NP

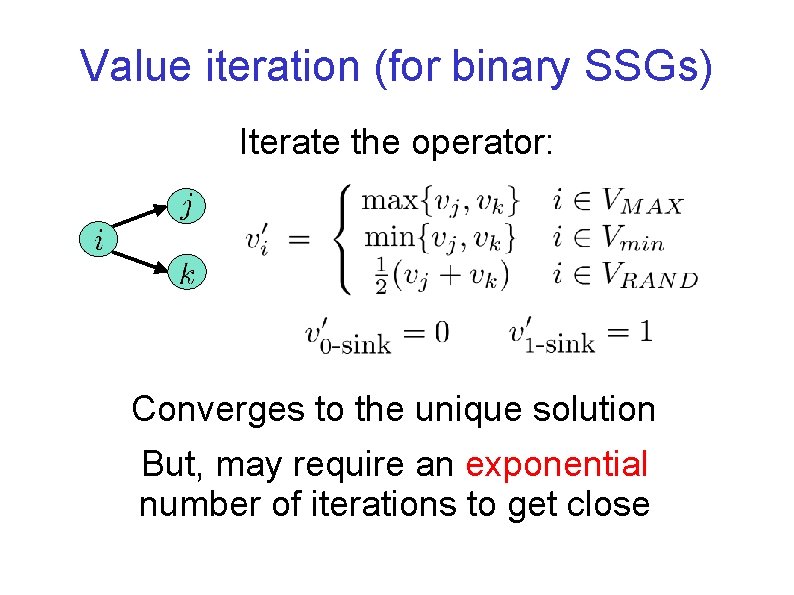
Value iteration (for binary SSGs) Iterate the operator: Converges to the unique solution But, may require an exponential number of iterations to get close

Simple Stochastic game (SSGs) Payoff version [Shapley (1953)] R MAX RAND min Limiting average version Discounted version

Markov Decision Processes (MDPs) R MAX RAND min Theorem: [Epenoux (1964)] Values and optimal strategies of a MDP can be found by solving an LP

SSG NP co-NP – Another proof Deciding whether the value of a game is at least (at most) v is in NP co-NP To show that value v , guess an optimal strategy for MAX Find an optimal counter-strategy for min by solving the resulting MDP. Is the problem in P ?

Mean Payoff Games (MPGs) [Ehrenfeucht, Mycielski (1979)] R MAX RAND min Non-terminating version Discounted version MPGs Payoff SSGs Reachability SSGs Pseudo-polynomial algorithm (PZ’ 96)

Mean Payoff Games (MPGs) [Ehrenfeucht, Mycielski (1979)] Again, both players have optimal positional strategies. Value(σ, ) – average of cycle formed

Selecting the second largest element with only four storage locations [PZ’ 96]

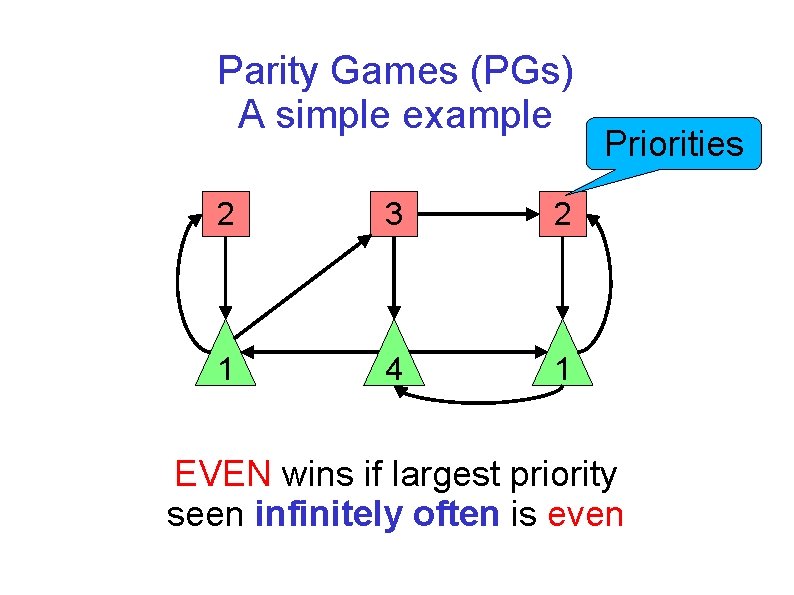
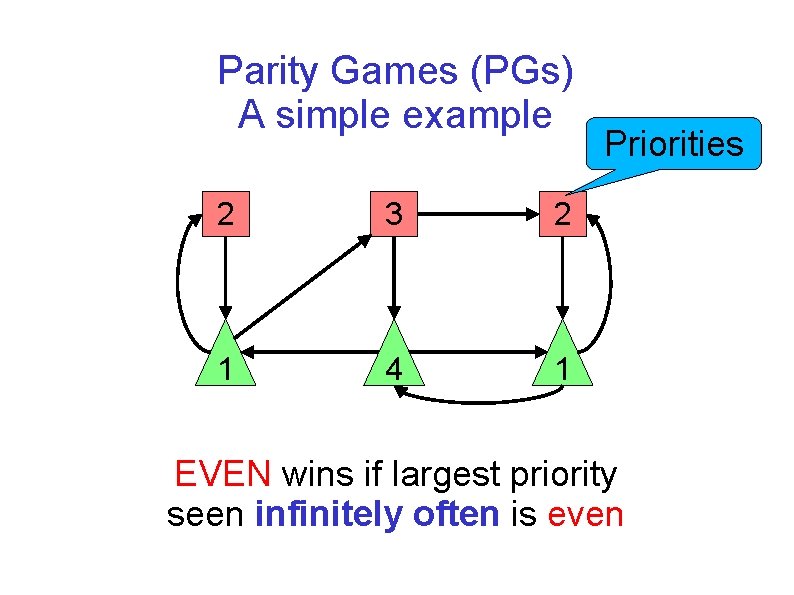
Parity Games (PGs) A simple example 2 3 2 1 4 1 Priorities EVEN wins if largest priority seen infinitely often is even

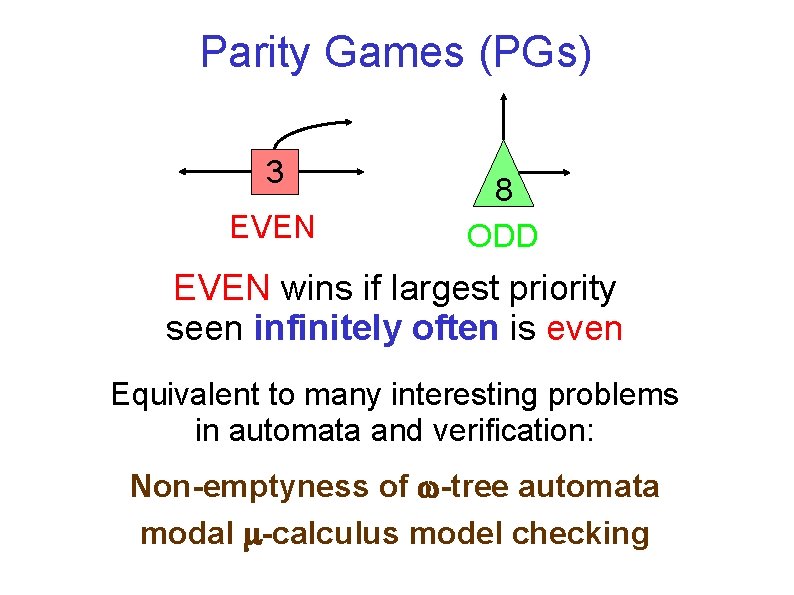
Parity Games (PGs) 3 EVEN 8 ODD EVEN wins if largest priority seen infinitely often is even Equivalent to many interesting problems in automata and verification: Non-emptyness of -tree automata modal -calculus model checking

Parity Games (PGs) Mean Payoff Games (MPGs) [Stirling (1993)] [Puri (1995)] 3 EVEN 8 ODD Replace priority k by payoff ( n)k Move payoffs to outgoing edges

Switches …

Strategy/Policy Iteration Start with some strategy σ (of MAX) While there are improving switches, perform some of them As each step is strictly improving and as there is a finite number of strategies, the algorithm must end with an optimal strategy SSG PLS (Polynomial Local Search)

Strategy/Policy Iteration Complexity? Performing only one switch at a time may lead to exponentially many improvements, even for MDPs [Condon (1992)] What happens if we perform all profitable switches [Hoffman-Karp (1966)] ? ? ? Not known to be polynomial O(2 n/n) [Mansour-Singh (1999)] No non-linear examples 2 n-O(1) [Madani (2002)]

A randomized subexponential algorithm for simple stochastic games

A randomized subexponential algorithm for binary SSGs [Ludwig (1995)] [Kalai (1992)] [Matousek-Sharir-Welzl (1992)] Start with an arbitrary strategy for MAX Choose a random vertex i VMAX Find the optimal strategy ’ for MAX in the game in which the only outgoing edge of i is (i, (i)) If switching ’ at i is not profitable, then ’ is optimal Otherwise, let ( ’)i and repeat

A randomized subexponential algorithm for binary SSGs [Ludwig (1995)] [Kalai (1992)] [Matousek-Sharir-Welzl (1992)] MAX vertices All correct ! Would never be switched ! There is a hidden order of MAX vertices under which the optimal strategy returned by the first recursive call correctly fixes the strategy of MAX at vertices 1, 2, …, i

The hidden order ui(σ) - the maximum sum of values of a strategy of MAX that agrees with σ on i

The hidden order Order the vertices such that Positions 1, . . , i were switched and would never be switched again

SSGs are LP-type problems [Halman (2002)] General (non-binary) SSGs can be solved in time Independently observed by [Björklund-Sandberg-Vorobyov (2005)] AUSO – Acyclic Unique Sink Orientations

SSGs GPLCP [Gärtner-Rüst (2005)] [Björklund-Svensson-Vorobyov (2005)] GPLCP Generalized Linear Complementary Problem with a P-matrix

A deterministic subexponential algorithm for parity games Mike Paterson Marcin Jurdzinski Uri Zwick

Parity Games (PGs) A simple example 2 3 2 1 4 1 Priorities EVEN wins if largest priority seen infinitely often is even

Parity Games (PGs) Mean Payoff Games (MPGs) [Stirling (1993)] [Puri (1995)] 3 EVEN 8 ODD Replace priority k by payoff ( n)k Move payoffs to outgoing edges

Exponential algorithm for PGs [Mc. Naughton (1993)] [Zielonka (1998)] First recursive call Lemma: (i) (ii) Vertices of highest priority (even) Vertices from which EVEN can force the game to enter A

Exponential algorithm for PGs [Mc. Naughton (1993)] [Zielonka (1998)] Second recursive call In the worst case, both recursive calls are on games of size n 1

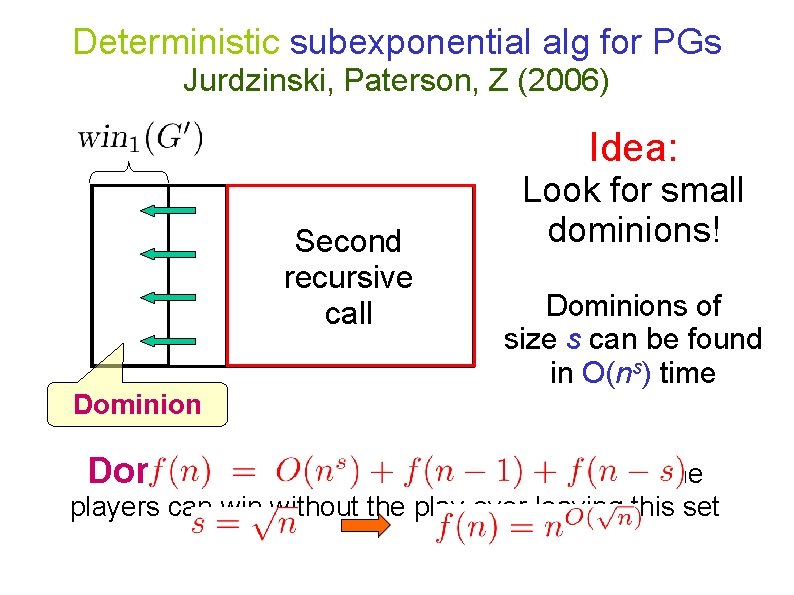
Deterministic subexponential alg for PGs Jurdzinski, Paterson, Z (2006) Idea: Second recursive call Dominion Look for small dominions! Dominions of size s can be found in O(ns) time Dominion: A (small) set from which one of the players can without the play ever leaving this set

Open problems ● ● ● Polynomial algorithms? Is the Policy Improvement algorithm polynomial? Faster subexponential algorithms for parity games? Deterministic subexponential algorithms for MPGs and SSGs? Faster pseudo-polynomial algorithms for MPGs?