Simple steps to analyse direct steps detection experiments

Simple steps to analyse direct steps detection experiments without halo uncertainties Felix Kahlhoefer Based on ar. Xiv: 1403. 4606 in collaboration with Brian Feldstein Rudolf Peierls Centre for Theoretical Physics APP Amsterdam, 23 June 2014

Introduction • A central problem in the analysis of direct detection experiments is the uncertainty in the dark matter velocity distribution f(v), which reduces the amount of information that can be inferred from a signal. • An isotropic Maxwell-Boltzmann distribution (the socalled Standard Halo Model) may not be a good approximation. • There is a great need for methods to combine information from different target materials in order to quantify and reduce the impact of these halo See talks by Bradley J. Kavanagh, Nassim Bozorgnia, uncertainties. Mattia Fornasa, and Chung-Lin Shan Felix Kahlhoefer APP Amsterdam, 23 June 2014 2

Standard approach • The standard approach is to propose a parameterization for f(v) and then study halo uncertainties by varying the underlying parameters. Peter, ar. Xiv: 0910. 4765, ar. Xiv: 1103. 5145; Pato (et al. ), ar. Xiv: 1106. 0743, ar. Xiv: 1211. 7063; Kavanag, Green, ar. Xiv: 1207. 2039, ar. Xiv: 1303. 6868 • It is, however, in general unclear whether the chosen parameterization is sufficiently general to account for localized features such as streams or debris flows. • An even greater problem arises from the fact that experimental predictions depend on the dark matter velocity distribution in a very complicated way. Felix Kahlhoefer APP Amsterdam, 23 June 2014 3

The rescaled velocity integral • In order to transfer the energy ER to a nucleus of mass m. N a dark matter particle must have a minimal velocity of • Defining the rescaled velocity integral we can then write the differential event rate for a given experiment in a very simple way: Felix Kahlhoefer APP Amsterdam, 23 June 2014 4

Predicted event rates • The event rate in a given bin of the form [Ei, Ei+1] is then found to be where εeff(ER) is the effective exposure and is the detector response function for energy resolution ΔER. Felix Kahlhoefer APP Amsterdam, 23 June 2014 5

A new method • To study how the experimental predictions Pi depend on f(v) a large number of numerical integrations is required, making the standard approach numerically slow. • Instead it is much more efficient to directly parameterize the velocity integral g(vmin). • We want to make no assumptions on the functional form of g(vmin) except that (as the integral of a positive distribution) it must be monotonically decreasing. • Basic idea: Decompose the velocity distribution into a large number of streams with different densities and speeds. Felix Kahlhoefer APP Amsterdam, 23 June 2014 6

A few simple steps 1. Ansatz: steps: is a piecewise constant function with Ns Monotonicity implies that . 2. For this ansatz we calculate the predicted event rates Pi(g) and define 3. Now we determine the values of gi that minimize χ2(g). 4. We repeat steps 1 -3 for increasing number of steps until the minimum of χ2(g) converges (in practice: Ns ~ 30). Felix Kahlhoefer APP Amsterdam, 23 June 2014 7

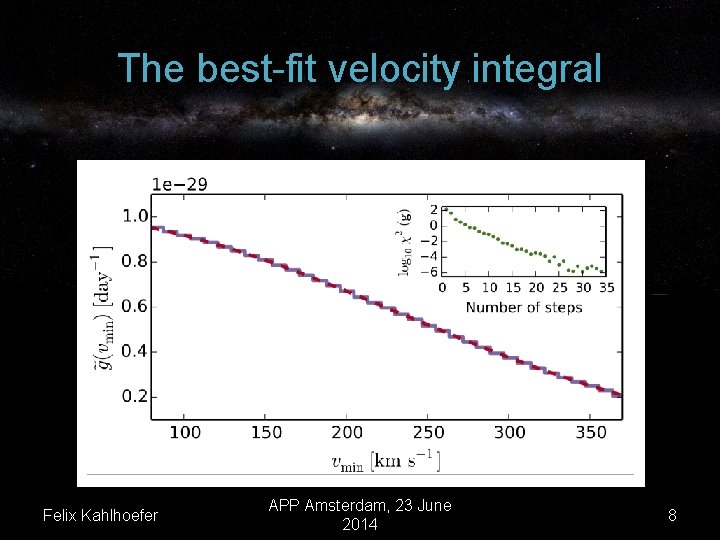
The best-fit velocity integral Best-fit approximation Standard Halo Model prediction for the velocity integral Felix Kahlhoefer APP Amsterdam, 23 June 2014 8

Numerical efficiency • Even for Ns ~ 30 the minimization takes only a few seconds. The reasons are that 1. Predictions depend linearly on the gi: where the coefficients are independent of the gi. 2. It can be shown that χ2(g) is a convex function of the gi, so that any local minimum is automatically a global one. Felix Kahlhoefer APP Amsterdam, 23 June 2014 9

Parameter estimation • Since any continuous function can be approximated arbitrarily well by a sum of step functions, our method effectively finds the best possible form for g(vmin). • We can repeat this minimization for a large set of different dark matter parameters to find the global minimum of χ2 and then calculate Δχ2 = χ2 – χ2 min. • In the presence of Poisson fluctuations, Δχ2 follows a χ2 distribution as usual, so the standard method can be used to calculate confidence intervals for the dark matter parameters. Felix Kahlhoefer APP Amsterdam, 23 June 2014 10

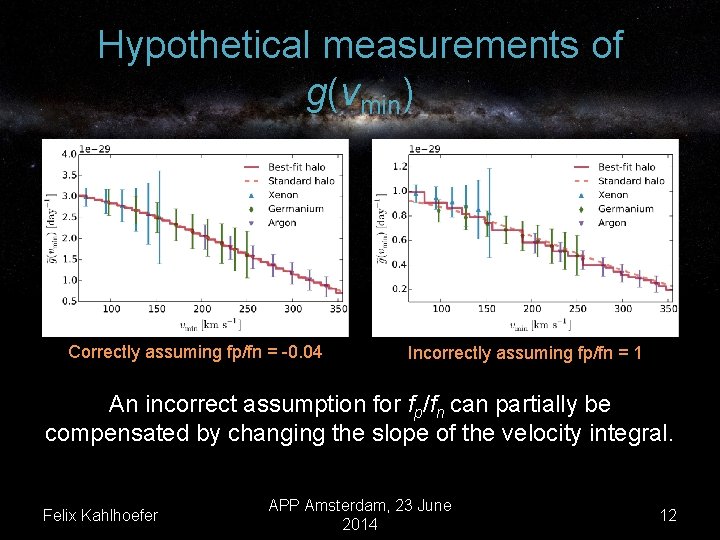
A closer look: Determination of fp/fn • Is it possible to distinguish fp/fn = 1 (Higgs mediation) from fp/fn = – 0. 04 (Z-boson mediation) using data from upcoming experiments? To find out why this is interesting, see talk by Brian Feldstein on Friday • Here we consider three different targets: Xe (A/Z = 2. 43), Ge (A/Z = 2. 27) and Ar (A/Z = 2. 22). • We generate mock data for a hypothetical set of future experiments for fp/fn = – 0. 04 and map this data onto vmin-space using and Felix Kahlhoefer APP Amsterdam, 23 June 2014 11

Hypothetical measurements of g(vmin) Correctly assuming fp/fn = -0. 04 Incorrectly assuming fp/fn = 1 An incorrect assumption for fp/fn can partially be compensated by changing the slope of the velocity integral. Felix Kahlhoefer APP Amsterdam, 23 June 2014 12

Testing the hypothesis fp/fn = 1 • Since the different experiments do not probe the same region of vmin-space, astrophysical uncertainties severely affect the determination of fp/fn. • Nevertheless, the different experiments have some overlap in vmin-space, allowing to extract relevant information in a halo-independent way. • For the example above, we find Δχ2 = 1. 05 so that the hypothesis fp/fn = 1 is disfavoured with 69% confidence. Felix Kahlhoefer APP Amsterdam, 23 June 2014 13

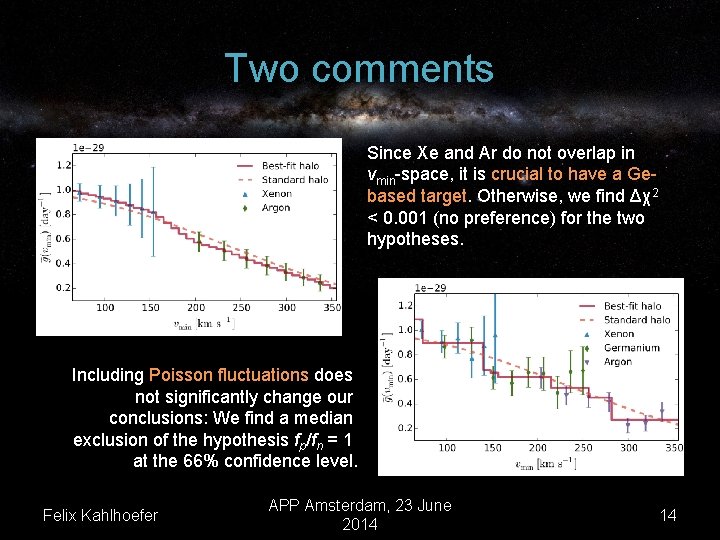
Two comments Since Xe and Ar do not overlap in vmin-space, it is crucial to have a Gebased target. Otherwise, we find Δχ2 < 0. 001 (no preference) for the two hypotheses. Including Poisson fluctuations does not significantly change our conclusions: We find a median exclusion of the hypothesis fp/fn = 1 at the 66% confidence level. Felix Kahlhoefer APP Amsterdam, 23 June 2014 14

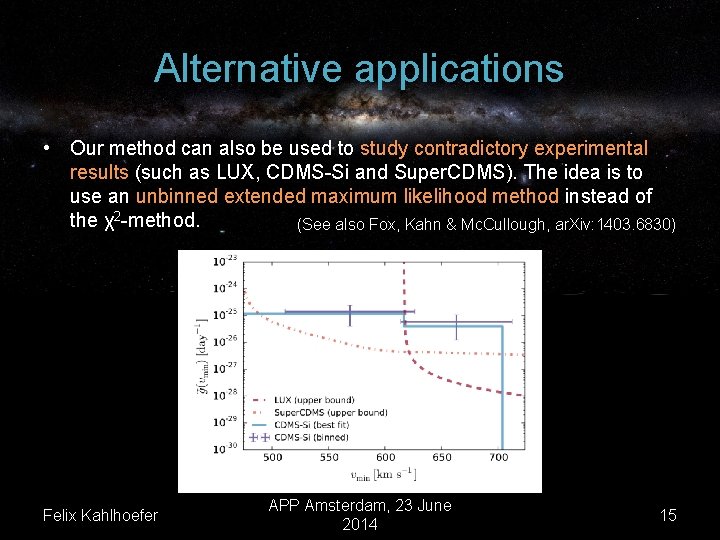
Alternative applications • Our method can also be used to study contradictory experimental results (such as LUX, CDMS-Si and Super. CDMS). The idea is to use an unbinned extended maximum likelihood method instead of the χ2 -method. (See also Fox, Kahn & Mc. Cullough, ar. Xiv: 1403. 6830) Felix Kahlhoefer APP Amsterdam, 23 June 2014 15

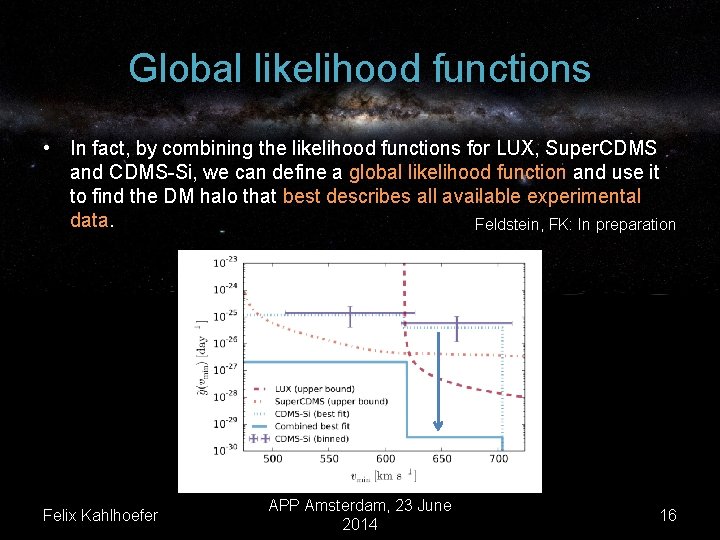
Global likelihood functions • In fact, by combining the likelihood functions for LUX, Super. CDMS and CDMS-Si, we can define a global likelihood function and use it to find the DM halo that best describes all available experimental data. Feldstein, FK: In preparation Felix Kahlhoefer APP Amsterdam, 23 June 2014 16

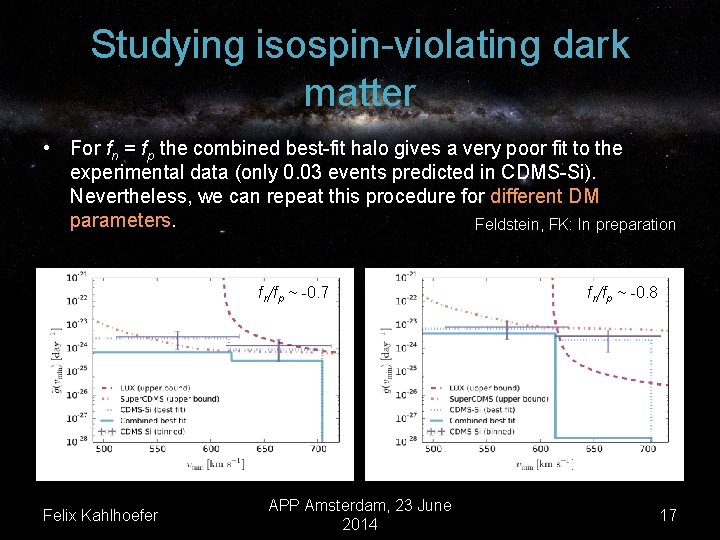
Studying isospin-violating dark matter • For fn = fp the combined best-fit halo gives a very poor fit to the experimental data (only 0. 03 events predicted in CDMS-Si). Nevertheless, we can repeat this procedure for different DM parameters. Feldstein, FK: In preparation fn/fp ~ -0. 7 Felix Kahlhoefer APP Amsterdam, 23 June 2014 fn/fp ~ -0. 8 17

Quantifying statistical significance • For both fn/fp ~ -0. 7 and fn/fp ~ -0. 8 the combined best-fit halo still gives a rather poor fit to the CDMS-Si data (only ~1 signal event predicted, Δlog(L) ~ 3 compared to the CDMS-Si best-fit halo). • Nevertheless, for both of these options the combined best-fit halo is clearly preferred over the background-only hypothesis (Δlog(L) ~ 8). • We can use this information to quantify the significance of the signal and the tension between different experiments in a halo-independent way. Felix Kahlhoefer APP Amsterdam, 23 June 2014 18

Outlook • Our method can be applied to more complicated particle physics models (e. g. inelastic dark matter or long-range interactions) as well as to annually modulating signals. • It would be very interesting to be able to make goodnessof-fit estimates based on χ2 min rather than only using Δχ2 for confidence intervals. • For the extended maximum likelihood method, a goodness-of-fit is not possible. Nevertheless, using Monte-Carlo simulations it should still be possible to quantify the p-value of the signal hypothesis. Felix Kahlhoefer APP Amsterdam, 23 June 2014 19

Backup Felix Kahlhoefer APP Amsterdam, 23 June 2014 20

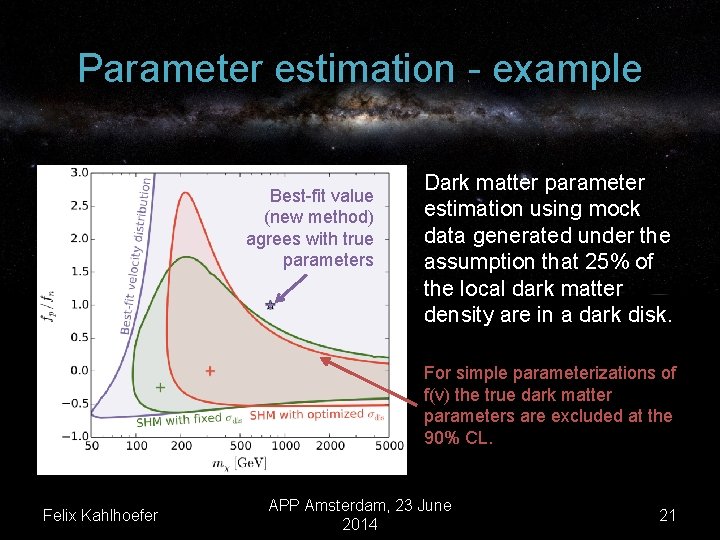
Parameter estimation - example Best-fit value (new method) agrees with true parameters Dark matter parameter estimation using mock data generated under the assumption that 25% of the local dark matter density are in a dark disk. For simple parameterizations of f(v) the true dark matter parameters are excluded at the 90% CL. Felix Kahlhoefer APP Amsterdam, 23 June 2014 21