SIMPLE MACHINES A simple machine is a mechanical

SIMPLE MACHINES A simple machine is a mechanical device that changes the direction or magnitude of a force. In general, they can be defined as the simplest mechanisms that use mechanical advantage (also called leverage) to multiply force.

Examples of Simple Machines • Usually the term refers to the six classical simple machines : • Lever • Wheel and axle • Inclined Plane • Wedge • Screw

LEVER • A lever is a simple machine consisting of a beam or rigid rod pivoted at a fixed hinge, or fulcrum. • A lever is a rigid body capable of rotating on a point on itself. • On the basis of the locations of fulcrum, load and effort, the lever is divided into three types

LEVER Levers can be used to exert a large force over a small distance at one end by exerting only a small force(effort) over a greater distance at the other.

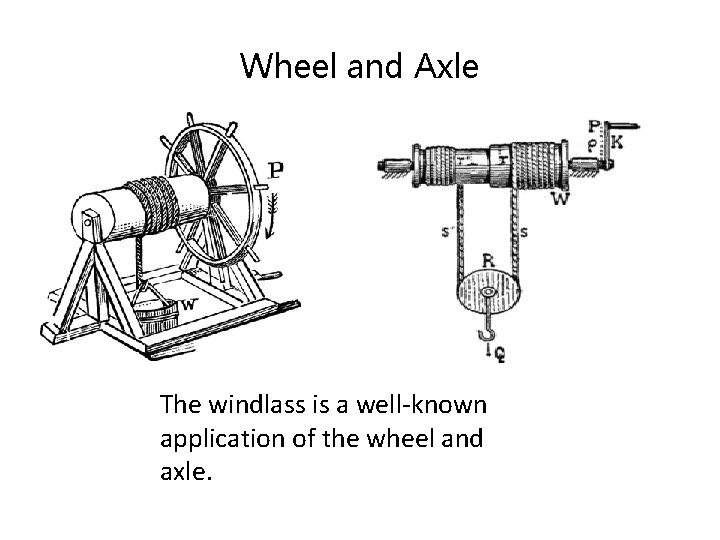
Wheel and Axle • The wheel and axle is a machine consisting of a wheel attached to a smaller axle so that these two parts rotate together in which a force is transferred from one to the other. • A hinge or bearing supports the axle, allowing rotation. • It can amplify force; a small force applied to the periphery of the large wheel can move a larger load attached to the axle.

Wheel and Axle The windlass is a well-known application of the wheel and axle.

Pulley • A pulley is a wheel on an axle or shaft that is designed to support movement and change of direction of a taut cable or belt, or transfer of power between the shaft and cable or belt. • In the case of a pulley supported by a frame or shell that does not transfer power to a shaft, but is used to guide the cable or exert a force, the supporting shell is called a block, and the pulley may be called a sheave. • A pulley may have a groove or grooves between flanges around its circumference to locate the cable or belt. The drive element of a pulley system can be a rope, cable, belt, or chain.

Pulleys on a ship. In this context, pulleys are normally known as blocks.

Wedge • A wedge is a triangular shaped tool, and is a portable inclined plane, and one of the six classical simple machines. • It can be used to separate two objects or portions of an object, lift up an object, or hold an object in place. • It functions by converting a force applied to its blunt end into forces perpendicular (normal) to its inclined surfaces.

Wedge A wood splitting wedge

SCREW • A screw is a mechanism that converts rotational motion to linear motion, and a torque (rotational force) to a linear force. • It is one of the six classical simple machines. The most common form consists of a cylindrical shaft with helical grooves or ridges called threads around the outside. • The screw passes through a hole in another object or medium, with threads on the inside of the hole that mesh with the screw's threads.

SCREW • When the shaft of the screw is rotated relative to the stationary threads, the screw moves along its axis relative to the medium surrounding it; for example rotating a wood screw forces it into wood. • In screw mechanisms, either the screw shaft can rotate through a threaded hole in a stationary object, or a threaded collar such as a nut can rotate around a stationary screw shaft. • Geometrically, a screw can be viewed as a narrow inclined plane wrapped around a cylinder.

SCREW A machine used in schools to demonstrate the action of a screw. It consists of a threaded shaft through a threaded hole in a stationary mount. When the crank on the right is turned, the shaft moves horizontally through the hole.

Mechanical Advantage • Mechanical advantage is a measure of the force amplification achieved by using a tool, mechanical device or machine system. • The device preserves the input power and simply trades off forces against movement to obtain a desired amplification in the output. • The performance of a real system relative to this ideal is expressed in terms of efficiency factors that take into account departures from the ideal.

Mechanical Advantage and Velocity Ratio: q Effort (FE) – Forced exerted on the machine. q Load (FL) – Forced on the output side of the machine Mechanical advantage: q Relationship between the load and the effort which gives an indication of the advantage that can be obtained by using the machine Mechanical Advantage = Load / Effort OR MA = FL / FE

Velocity Ratio • The requirement for power input to an ideal mechanism to equal power output provides a simple way to compute mechanical advantage from the input-output speed ratio of the system. • The power input to a gear train with a torque T applied to the drive pulley which rotates at an angular velocity of ω is P=Tω. • Because the power flow is constant, the torque T and angular velocity ω of the output gear must satisfy the relation

Velocity Ratio This shows that for an ideal mechanism the inputoutput speed ratio equals the mechanical advantage of the system. This applies to all mechanical systems ranging from robots to linkages.

Velocity Ratio q Ratio of the distance moved through by the effort on the input side (SE) to the distance moved through by the load on the output side (SL) Velocity Ratio = distance moved by Effort / distance moved by load OR VR = SE / SL

Work and Efficiency: q (Input side) Work done by the Effort: Work done by Effort (WE) = FE X SE q (Output side) Work done in moving the Load: q Efficiency : Eff. = WL /WE WL = FL X SL

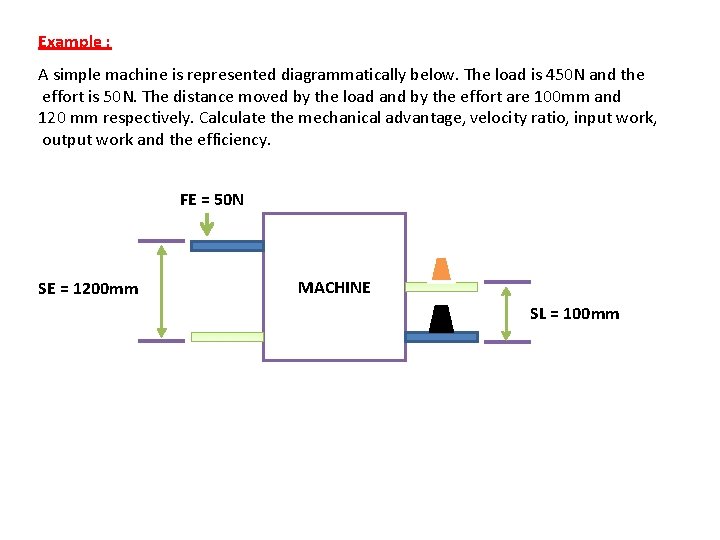
Example : A simple machine is represented diagrammatically below. The load is 450 N and the effort is 50 N. The distance moved by the load and by the effort are 100 mm and 120 mm respectively. Calculate the mechanical advantage, velocity ratio, input work, output work and the efficiency. FE = 50 N SE = 1200 mm MACHINE SL = 100 mm

Solution: a. Mechanical advantage: q MA = FL / FE = 450 N /50 N =9 b. Velocity Ratio: q VR = SE / SL = 1200 mm /100 mm = 12 c. Input work: q WE = 50 N X 1. 2 m = 60 J d. Output work: q WL = 450 N X 0. 1 m = 45 J e. Efficiency: q Eff. = WL / WE = 45 /60 = 0. 75 = 75% Efficiency is expressed as %. Actually machines efficiency is always less than 100%