Simple Linear Regression Often we want to understand

Simple Linear Regression Often we want to understand the relationships among variables, e. g. , SAT scores and college GPA car weight and gas mileage amount of a certain pollutant in wastewater and bacteria growth in local streams number of takeoffs and landings and degree of metal fatigue in aircraft structures Simplest relationship Y = β 0 + β 1 x 1 ETM 620 - 09 U

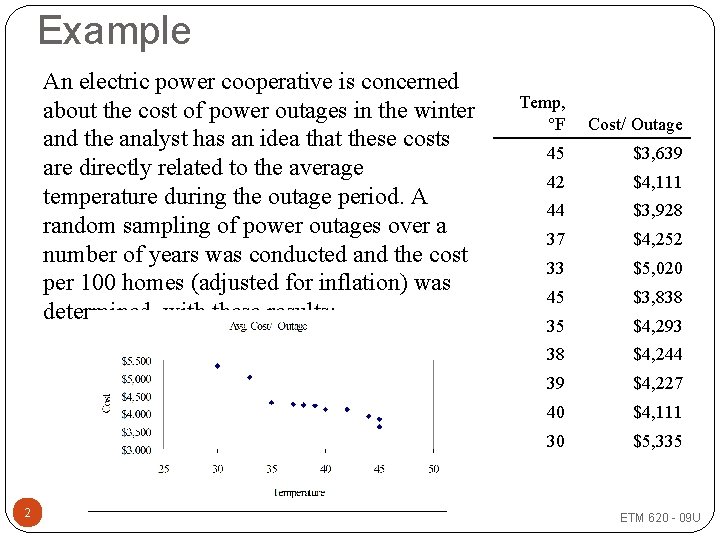
Example An electric power cooperative is concerned about the cost of power outages in the winter and the analyst has an idea that these costs are directly related to the average temperature during the outage period. A random sampling of power outages over a number of years was conducted and the cost per 100 homes (adjusted for inflation) was determined, with these results: 2 Temp, °F Cost/ Outage 45 $3, 639 42 $4, 111 44 $3, 928 37 $4, 252 33 $5, 020 45 $3, 838 35 $4, 293 38 $4, 244 39 $4, 227 40 $4, 111 30 $5, 335 ETM 620 - 09 U

Estimating the regression coefficients Method of Least Squares Determine estimates for β 0 and β 1 so that the sum of the squares of the residuals is minimized, that is … Solution to the minimization gives: 3 ETM 620 - 09 U

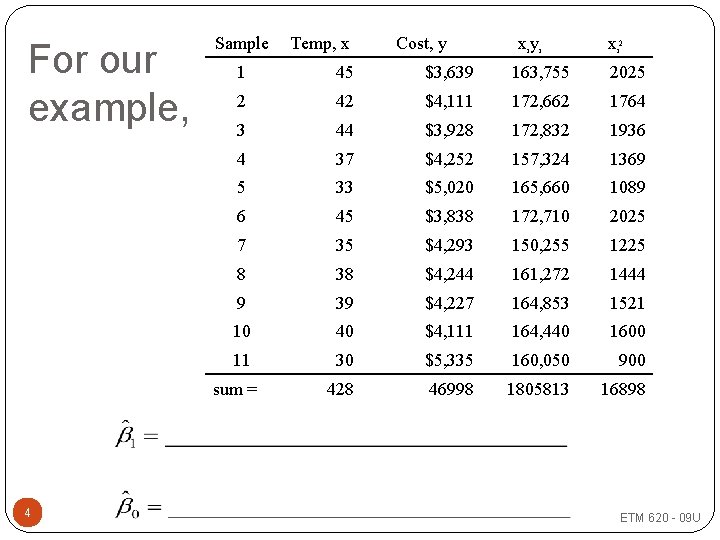
For our example, Sample Cost, y xiyi xi 2 1 45 $3, 639 163, 755 2025 2 42 $4, 111 172, 662 1764 3 44 $3, 928 172, 832 1936 4 37 $4, 252 157, 324 1369 5 33 $5, 020 165, 660 1089 6 45 $3, 838 172, 710 2025 7 35 $4, 293 150, 255 1225 8 38 $4, 244 161, 272 1444 9 39 $4, 227 164, 853 1521 10 40 $4, 111 164, 440 1600 11 30 $5, 335 160, 050 900 428 46998 1805813 16898 sum = 4 Temp, x ETM 620 - 09 U

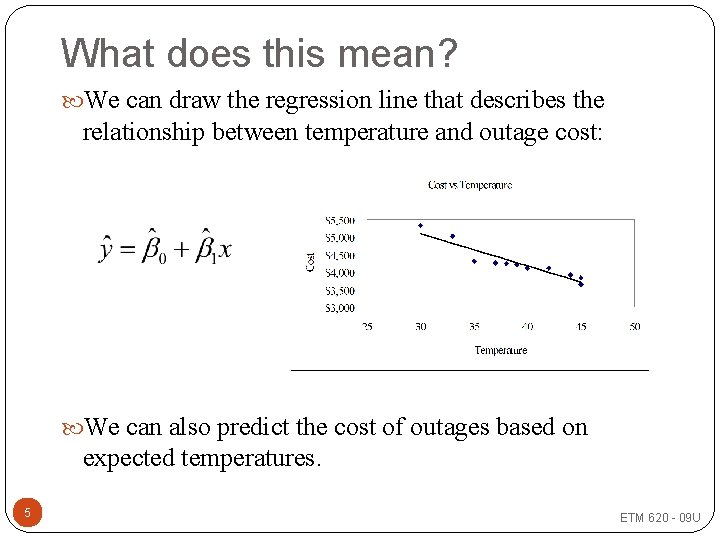
What does this mean? We can draw the regression line that describes the relationship between temperature and outage cost: We can also predict the cost of outages based on expected temperatures. 5 ETM 620 - 09 U

Dangers of regression analysis You can regress any variable on any other variable e. g. , hair loss and heart disease; hours playing video games and number of arrests for violent behavior; consecutive hours in class and retention of material; etc. Which of these relationships can you legitimately claim reflect a causal relationship between the “predictor” and the “response”? The regression equation is a “best fit” for the data on which it is based, but may lose validity for predictor values outside the range of the data. For example, our outage cost data implies that the 6 cost per outage decreases as the temperature increases – do you believe that temperatures in ETM the 620 - 09 U

How good is our prediction? Estimating the variance: Lack of fit test, Tests the hypotheses H 0: the model adequately fits the data H 1: the model does not fit the data As with our goodness-of-fit tests, a high p-value indicates that the model is adequate. 7 (see next page) ETM 620 - 09 U

How good is our prediction? • Coefficient of determination, R 2 a measure of the “quality of fit, ” or the proportion of the variability explained by the fitted model. Use with care – increasing the number of variables will usually increase R 2, but this doesn’t necessarily make it a “better” model! 8 ETM 620 - 09 U

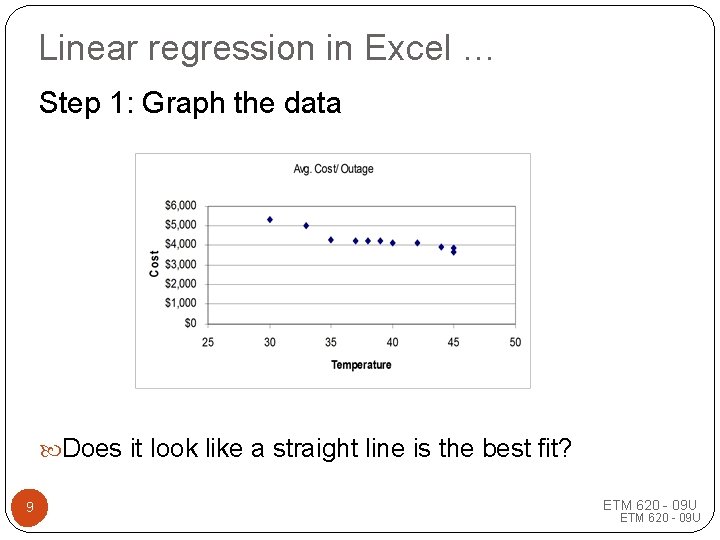
Linear regression in Excel … Step 1: Graph the data Does it look like a straight line is the best fit? 99 ETM 620 - 09 U

Step 2: Perform the analysis Choose “Regression” from the Data Analysis menu (under Tools). Input the Y-range (Cost, including the label) and X-range (Temp, including the label), then select “Labels” if you included those in your data range. Your desired location for the output. Residuals and Normal Probability Plot, as desired. Choose “OK” 10 ETM 620 - 09 U

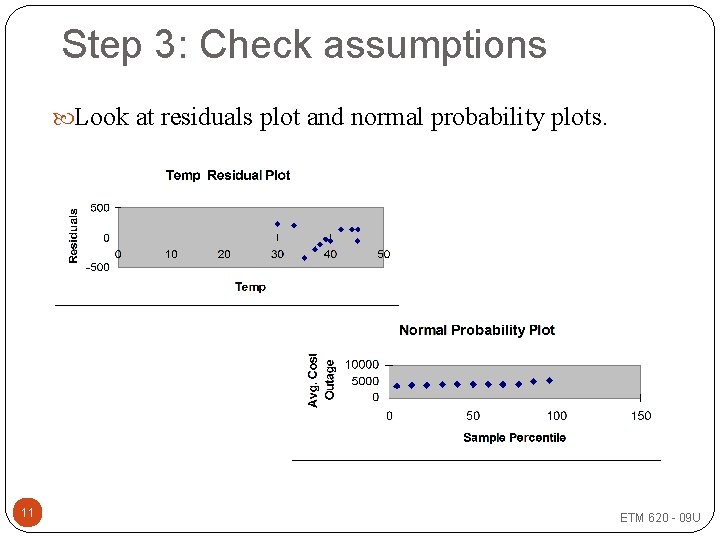
Step 3: Check assumptions Look at residuals plot and normal probability plots. 11 ETM 620 - 09 U

Step 4. Evaluate the results. 12 ETM 620 - 09 U

Step 5. Specify and use the model. Simple linear model: Use the model to: Make predictions expected costs budgeting Recommend actions identify and address sources of cost increase 13 ETM 620 - 09 U

In Minitab … Step 1: Graph the data (for one or two predictor variables)! Again, do you think a simple linear relationship is the best fit? Step 2: Select Stat Regression … Step 3: Choose “Response” (y) and “Predictor” (x). Step 4: In “Options”, check the “Lack of Fit” box. (“Fit Intercept” box should be checked by default. ) Click “OK”. Step 6: In “Graphs” select the appropriate residual plots to create. Step 5: Click “OK”. Step 6: Evaluate the residual plots and results. 14 ETM 620 - 09 U

Transformation to a straight line. . , If simple linear regression is not appropriate because the underlying function is nonlinear, then we have two choices fit a more complex model transform the model to a straight-line model Simplest transformation – logarithmic transformation Original model: Transformed model: 15 ETM 620 - 09 U