Simple Linear Regression 1 Introduction In Chapter we

Simple Linear Regression 1

Introduction • In Chapter we examine the relationship between interval variables via a mathematical equation. • The motivation for using the technique: – Forecast the value of a dependent variable (y) from the value of independent variables (x 1, x 2, …xk. ). – Analyze the specific relationships between the independent variables and the 2 dependent variable.

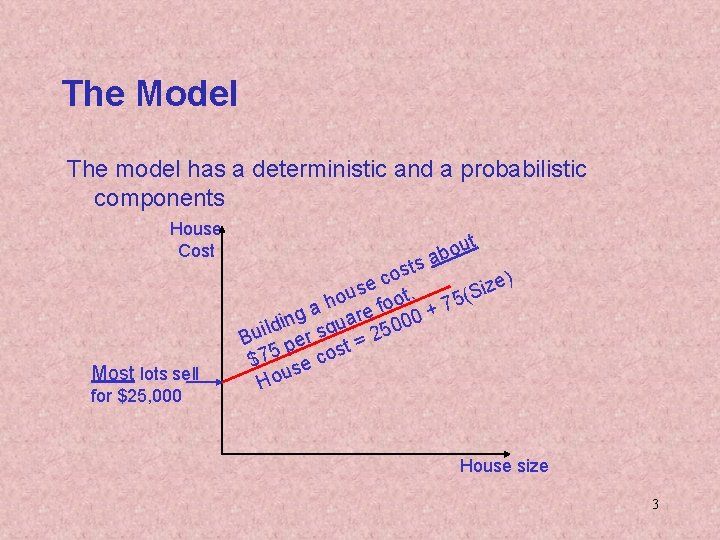
The Model The model has a deterministic and a probabilistic components House Cost Most lots sell for $25, 000 t u o ab ts s o c e) e z i s hou foot. + 75(S a re 00 g a n i u 0 ld q Bui per s t = 25 s $75 se co House size 3

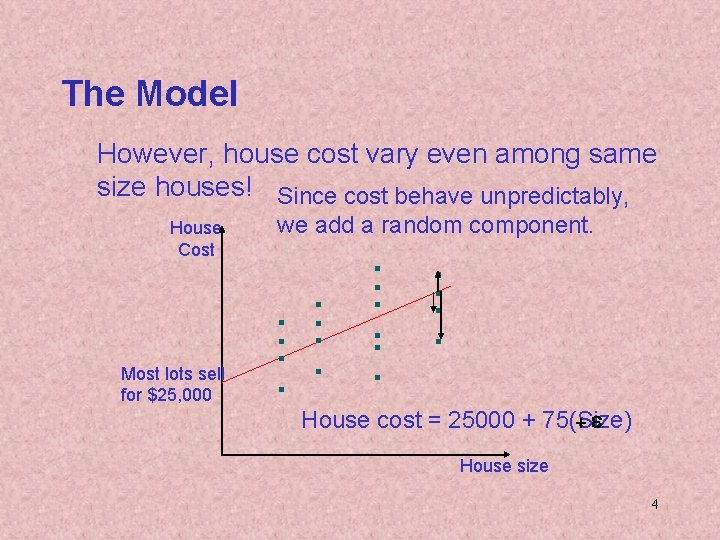
The Model However, house cost vary even among same size houses! Since cost behave unpredictably, House Cost Most lots sell for $25, 000 we add a random component. +e House cost = 25000 + 75(Size) House size 4

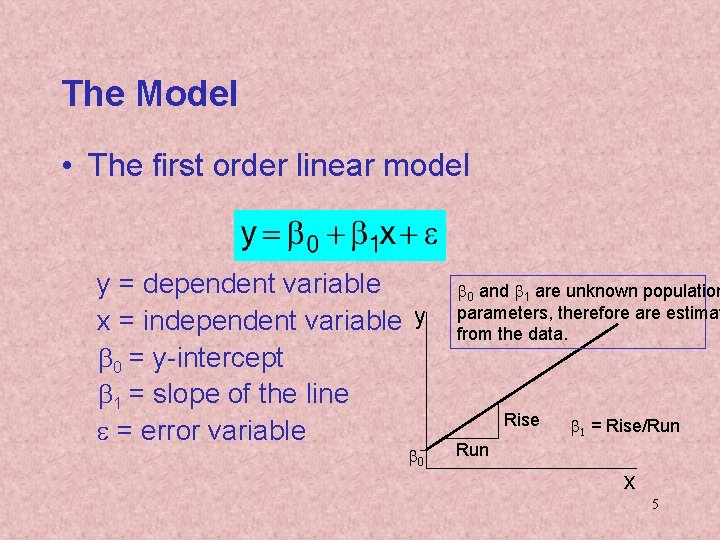
The Model • The first order linear model y = dependent variable x = independent variable y b 0 = y-intercept b 1 = slope of the line e = error variable b 0 and b 1 are unknown population parameters, therefore are estimat from the data. Rise b 1 = Rise/Run x 5

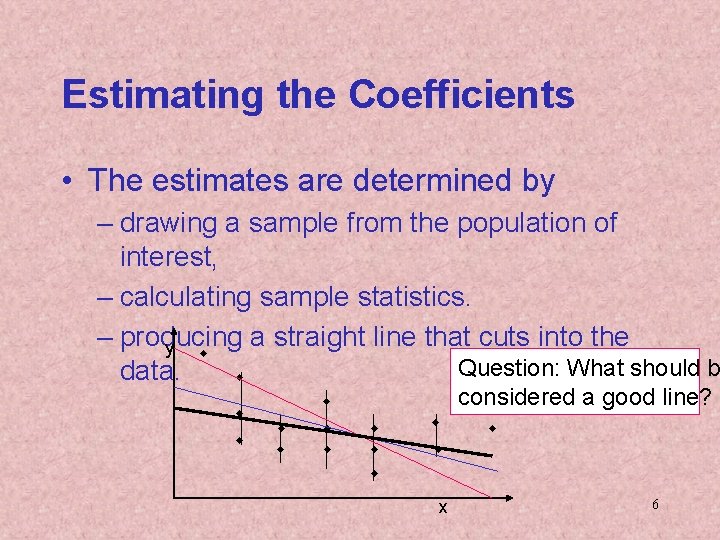
Estimating the Coefficients • The estimates are determined by – drawing a sample from the population of interest, – calculating sample statistics. – producing a straight line that cuts into the y w Question: What should b data. w w w considered a good line? w w w x 6

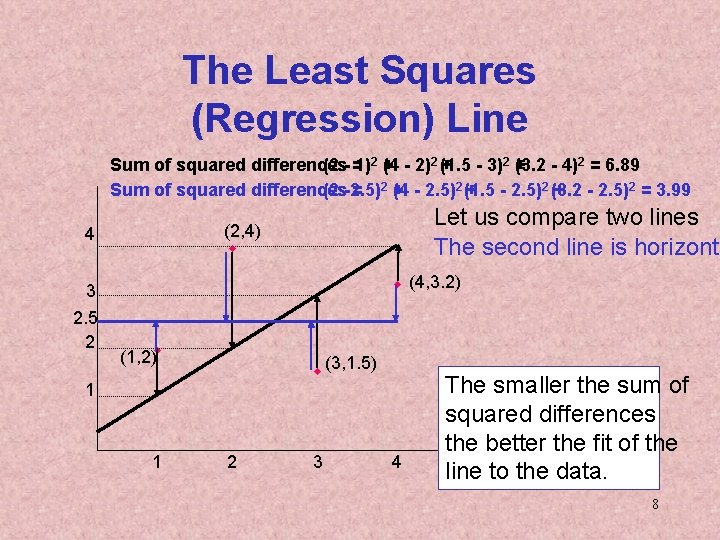
The Least Squares (Regression) Line A good line is one that minimizes the sum of squared differences between the points and the line. 7

The Least Squares (Regression) Line Sum of squared differences (2 - =1)2 + (4 - 2)2 (+1. 5 - 3)2 + (3. 2 - 4)2 = 6. 89 Sum of squared differences (2 -2. 5) = 2+ (4 - 2. 5)2 (+1. 5 - 2. 5)2 (3. 2 + - 2. 5)2 = 3. 99 3 2. 5 2 Let us compare two lines The second line is horizonta (2, 4) w 4 w (4, 3. 2) (1, 2)w w (3, 1. 5) 1 1 2 3 4 The smaller the sum of squared differences the better the fit of the line to the data. 8

The Estimated Coefficients To calculate the estimates of the line coefficients, that minimize the differences between the data points and the line, use the formulas: The regression equation that estimate the equation of the first order linear m is: 9

The Simple Linear Regression Line • Example 17. 2 (Xm 17 -02) – A car dealer wants to find the relationship between the odometer reading and the selling price of used cars. – A random sample of 100 cars is selected, Independent. Dependent variable x variable y 10

The Simple Linear Regression Line • Solution – Solving by hand: Calculate a number of statistics where n = 100. 11

The Simple Linear Regression Line • Solution – continued – Using the computer (Xm 17 -02) Tools > Data Analysis > Regression > [Shade the y range and the x range] > OK 12

The Simple Linear Regression Line Xm 17 -02 13

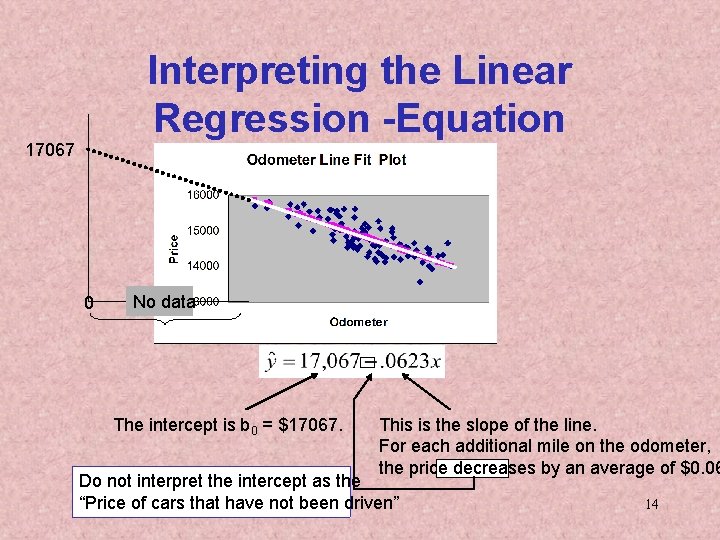
Interpreting the Linear Regression -Equation 17067 0 No data The intercept is b 0 = $17067. This is the slope of the line. For each additional mile on the odometer, the price decreases by an average of $0. 06 Do not interpret the intercept as the “Price of cars that have not been driven” 14

Error Variable: Required Conditions • The error e is a critical part of the regression model. • Four requirements involving the distribution of e must be satisfied. – The probability distribution of e is normal. – The mean of e is zero: E(e) = 0. – The standard deviation of e is se for all values of x. – The set of errors associated with different 15

The Normality of e E(y|x 3) The standard deviation remains constant, m 3 b 0 + b 1 x 3 E(y|x 2) b 0 + b 1 x 2 m 2 1) but the mean value changes with E(y|x x b 0 + b 1 x 1 m 1 From the first three assumptions we x 1 have: y is normally distributed with mean E(y) = b 0 + b 1 x, and a constant standard deviation se x 2 x 3 16

Assessing the Model • The least squares method will produces a regression line whether or not there are linear relationship between x and y. • Consequently, it is important to assess how well the linear model fits the data. • Several methods are used to assess the model. All are based on the sum of squares for errors, SSE. 17

Sum of Squares for Errors – This is the sum of differences between the points and the regression line. – It can serve as a measure of how well the line fits the data. SSE is defined by – A shortcut formula 18

Standard Error of Estimate – The mean error is equal to zero. – If se is small the errors tend to be close to zero (close to the mean error). Then, the model fits the data well. – Therefore, we can, use se as a measure of the suitability of using a linear model. – An estimator of se is given by se 19

Standard Error of Estimate, Example • Example 17. 3 – Calculate the standard error of estimate for Example 17. 2, and describe what does it tell you about the model fit? • Solution Calculated before It is hard to assess the model ba on se even when compared with mean value of y. 20

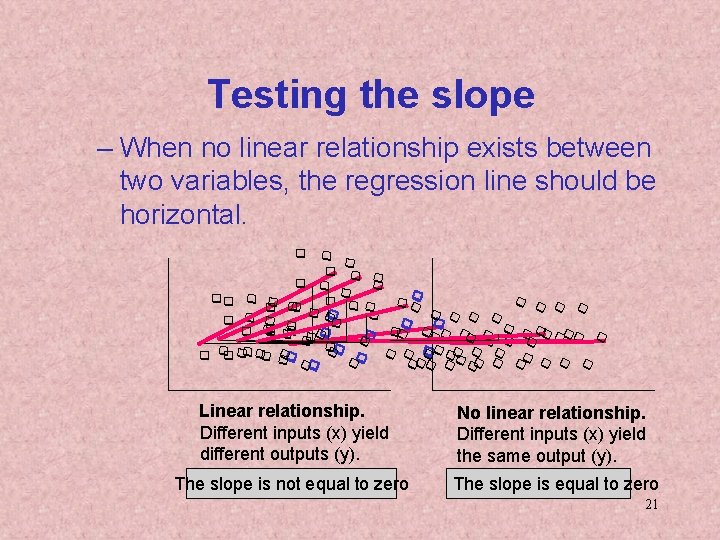
Testing the slope – When no linear relationship exists between two variables, the regression line should be horizontal. q q qq q q q q q q qq qq q q q qq qqq q q q q qq q q qq qq qqq q qq Linear relationship. Different inputs (x) yield different outputs (y). No linear relationship. Different inputs (x) yield the same output (y). The slope is not equal to zero The slope is equal to zero 21

Testing the Slope • We can draw inference about b 1 from b 1 by testing H 0: b 1 = 0 H 1: b 1 = 0 (or < 0, or > 0) – The test statistic is where The standard error of b 1. – If the error variable is normally distributed, 22 the statistic is Student t distribution with d. f. = n-2.

Testing the Slope, Example • Example 17. 4 – Test to determine whethere is enough evidence to infer that there is a linear relationship between the car auction price and the odometer reading for all three-year -old Tauruses, in Example 17. 2. Use a = 5%. 23

Testing the Slope, Example • Solving by hand – To compute “t” we need the values of b 1 and sb 1. – The rejection region is t > t. 025 or t < -t. 025 with n = n -2 = 98. Approximately, t. 025 = 1. 984 24

Testing the Slope, Example. Xm 17 -02 • Using the computer There is overwhelming evidence to infer that the odometer reading affects the auction selling price. 25

Coefficient of determination – To measure the strength of the linear relationship we use the coefficient of determination. 26

Coefficient of determination • To understand the significance of this coefficient note: ed n i a l xp Ey Overall variability in Rem ains y b. The t r a in p , in p art, u n expl regression model d. The aine error 27

Coefficient of determination y 2 Two data points (x 1, y 1) and (x 2, y 2) of a certain sample are shown. y y 1 Variation in y = SSR + SSE x 1 x 2 Variation explained by + Unexplained variation (error) Total variation in y = the regression line 28

Coefficient of determination • R 2 measures the proportion of the variation in y that is explained by the variation in x. • R 2 takes on any value between zero and one. R 2 = 1: Perfect match between the line and the 29 data points.

Coefficient of determination, Example • Example 17. 5 – Find the coefficient of determination for Example 17. 2; what does this statistic tell you about the model? • Solution – Solving by hand; 30

Coefficient of determination – Using the computer From the regression output we have 65% of the variation in the auction selling price is explained by the variation in odometer reading. The rest (35%) remains unexplained by this model. 31

17. 6 Finance Application: Market Model • One of the most important applications of linear regression is the market model. • It is assumed that rate of return on a stock (R) is linearly related to the rate of return on the overall market. R = b 0 + b 1 Rm +e Rate of return on a particular stock Rate of return on some major stock ind The beta coefficient measures how sensitive the stock’s rate of return is to changes in the level of the overall market. 32

The Market Model, Example 17. 6 (Xm 17 -06) • Estimate the market model for Nortel, a stock traded in the Toronto Stock Exchange (TSE). • Data consisted of monthly percentage This is a measure of the return for Nortel and monthly percentage stock’s return. This for all stocks. is athe measure of the total market-related ri market related risk. In this sample, for each 1% increase in the TSE return, the average increase in Nortel’s return is. 8877%. embedded in the Nortel stock. Specifically, 31. 37% of the variation in Nortel’s return are explained by the variation in the TSE’s returns. 33

Using the Regression Equation • Before using the regression model, we need to assess how well it fits the data. • If we are satisfied with how well the model fits the data, we can use it to predict the values of y. • To make a prediction we use – Point prediction, and – Interval prediction 34

Point Prediction • Example 17. 7 – Predict the selling price of a three-year-old Taurus with 40, 000 miles on the odometer (Example 17. 2). A point prediction – It is predicted that a 40, 000 miles car would sell for $14, 575. – How close is this prediction to the real price? 35

Interval Estimates • Two intervals can be used to discover how closely the predicted value will match the true value of y. – Prediction interval – predicts y for a given value of x, – Confidence interval – estimates average y for a – The prediction – Thetheconfidence given x. interval 36

Interval Estimates, Example • Example 17. 7 - continued – Provide an interval estimate for the bidding price on a Ford Taurus with 40, 000 miles on the odometer. – Two types of predictions are required: • A prediction for a specific car • An estimate for the average price per car 37

Interval Estimates, Example • Solution – A prediction interval provides the price estimate for a single car: t. 025, 98 Approximat ely 38

Interval Estimates, Example • Solution – continued – A confidence interval provides the estimate of the mean price per car for a Ford Taurus with 40, 000 miles reading on the odometer. • The confidence interval (95%) = 39

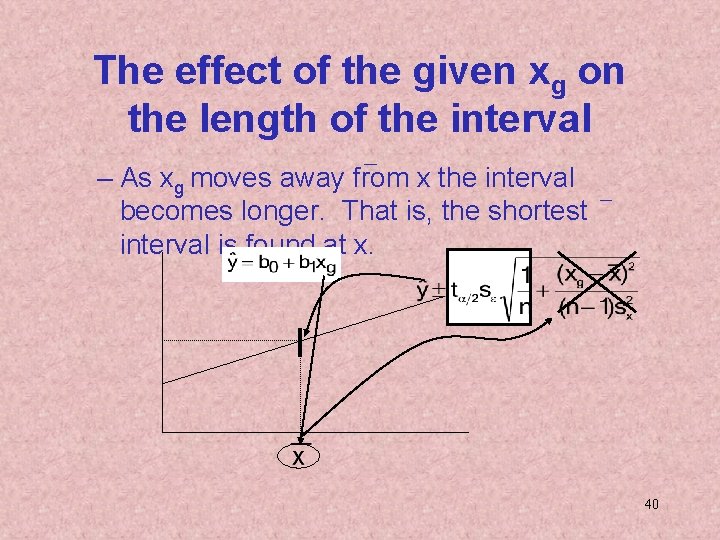
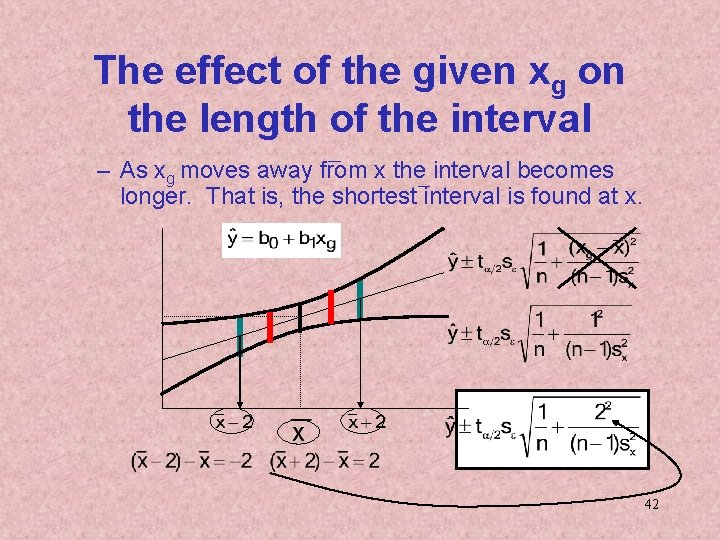
The effect of the given xg on the length of the interval – As xg moves away from x the interval becomes longer. That is, the shortest interval is found at x. 40

The effect of the given xg on the length of the interval – As xg moves away from x the interval becomes longer. That is, the shortest interval is found at x. 41

The effect of the given xg on the length of the interval – As xg moves away from x the interval becomes longer. That is, the shortest interval is found at x. 42

Coefficient of Correlation • The coefficient of correlation is used to measure the strength of association between two variables. • The coefficient values range between -1 and 1. – If r = -1 (negative association) or r = +1 (positive association) every point falls on the regression line. – If r = 0 there is no linear pattern. 43

Testing the coefficient of correlation • To test the coefficient of correlation for linear relationship between X and Y – X and Y must be observational – X and Y are bivariate normally distributed Y X 44

Testing the coefficient of correlation • When no linear relationship exist between the two variables, r = 0. • The hypotheses are: H 0: r = 0 H 1: r ¹ 0 • The test statistic is: The statistic is Student t distributed with d. f. = n 2, provided the variables are bivariate normally distributed. 45

Testing the Coefficient of correlation • Foreign Index Funds (Index) – A certain investor prefers the investment in an index mutual funds constructed by buying a wide assortment of stocks. – The investor decides to avoid the investment in a Japanese index fund if it is strongly correlated with an American index fund that he owns. – From the data shown in Index. xls should he avoid the investment in the Japanese index 46 fund?

Testing the Coefficient of correlation • Foreign Index Funds – A certain investor prefers the investment in an index mutual funds constructed by buying a wide assortment of stocks. – The investor decides to avoid the investment in a Japanese index fund if it is strongly correlated with an American index fund that he owns. – From the data shown in Index. xls should he avoid the investment in the Japanese index 47 fund?

Testing the Coefficient of Correlation, Example • Solution – Problem objective: Analyze relationship between two interval variables. – The two variables are observational (the return for each fund was not controlled). – We are interested in whethere is a linear relationship between the two variables, thus, we need to test the coefficient of correlation 48

Testing the Coefficient of Correlation, Example • Solution – continued – The hypotheses H 0: r = 0 H 1: r ¹ 0. – Solving by hand: The value of the t statistic is Conclusion: There is sufficient evidence at a = 5% to infer tha there are linear relationship • The rejection region: |t| > ta/2, n-2 = t. 025, 59 -2 » 2. 000. between the two variables. • The sample coefficient of correlation: Cov(x, y) =. 001279; sx =. 0509; sy = 0512 r = cov(x, y)/sxsy=. 491 49

Testing the Coefficient of Correlation, Example – Excel solution (Index) 50