Simple Linear Regression 1 1 Introduction Example David

Simple Linear Regression 1

1. Introduction Example: David Beckham: 1. 83 m Victoria Beckham: 1. 68 m ● Brad Pitt: 1. 83 m Angelina Jolie: 1. 70 m George Bush : 1. 81 m Laura Bush: ? To predict height of the wife in a couple, based on the husband’s height Response (out come or dependent) variable (Y): height of the wife Predictor (explanatory or independent) variable (X): height of the husband 2

Regression analysis: regression analysis is a statistical methodology to estimate the relationship of a response variable to a set of predictor variable. ●　 when there is just one predictor variable, we will use simple linear regression. When there are two or more predictor variables, we use multiple linear regression. ●　 when it is not clear which variable represents a response and which is a predictor, correlation analysis is used to study the strength of the relationship ● History: The earliest form of linear regression was the method of least squares, which was published by Legendre in 1805, and by Gauss in 1809. ● The method was extended by Francis Galton in the 19 th century to describe a biological phenomenon. ● This work was extended by Karl Pearson and Udny Yule to a more general statistical context around 20 th century. ● 3

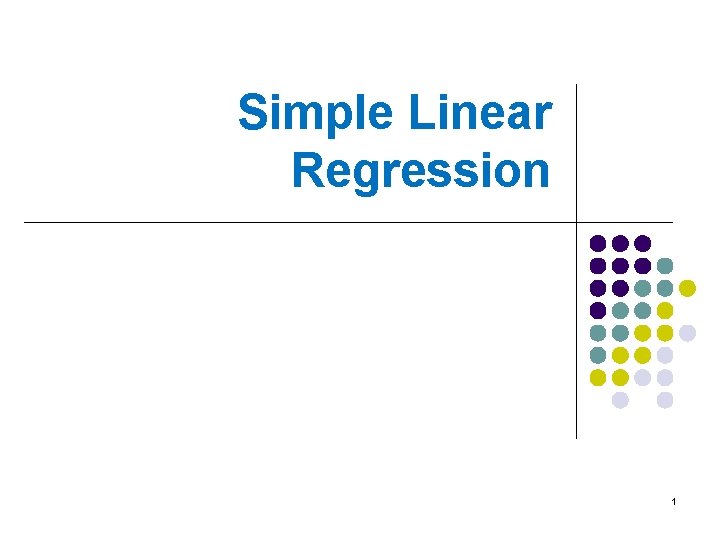
A probabilistic model l We denote the n observed values of the predictor variable x as l We denote the corresponding observed values of the response variable Y as 4

Notations of the simple linear Regression - Observed value of the random variable Yi depends on xi - random error with unknown mean of Yi True Regression Line Unknown Slope Unknown Intercept 5

Simple Linear Regression Model y = dependent variable x = independent variable b 0 = intercept b 1 = slope of the line = error variable y b 0 and b 1 are unknown, therefore, are estimated from the data. Rise b 0 b 1 = Rise/Run x 6

7

4 BASIC ASSUMPTIONS – for statistical inference Linear function of the predictor variable Have a common variance, Same for all values of x. Normally distributed Independent 8

Comments: 1. Linear not in x But in the parameters and Example: linear, logx = x* 2. Predictor variable is not set as predetermined fixed values, is random along with Y. The model can be considered as a conditional model Example: Height and Weight of the children. Height (X) – given Weight (Y) – predict Conditional expectation of Y given X = x 9

2. Fitting the Simple Linear Regression Model 2. 1 Least Squares (LS) Fit 10

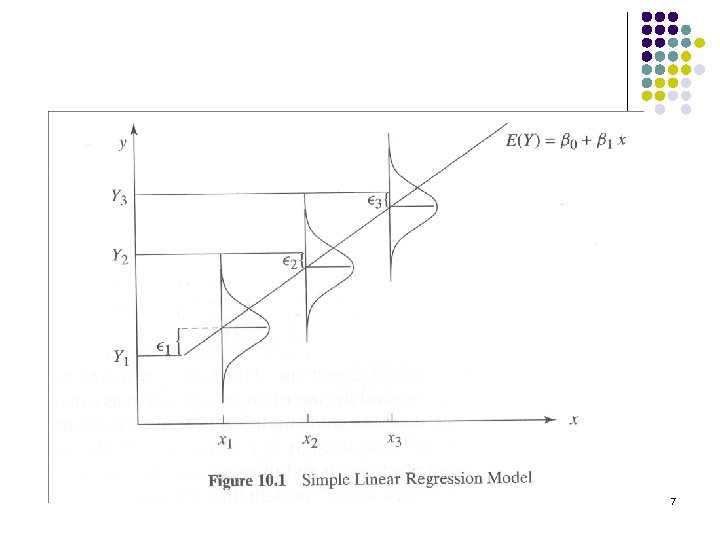
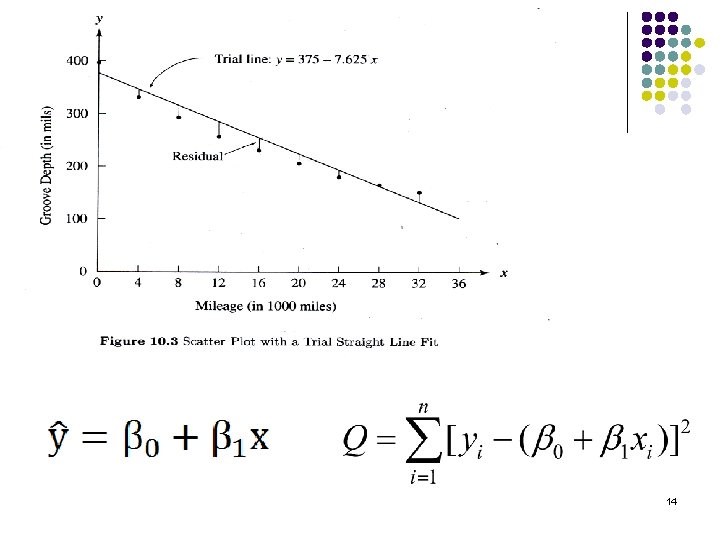
Example 10. 1 (Tires Tread Wear vs. Mileage: Scatter Plot. From: Statistics and Data Analysis; Tamhane and Dunlop; Prentice Hall. ) 11

Estimating the Coefficients l The estimates are determined by l l l drawing a sample from the population of interest, calculating sample statistics. producing a straight line that cuts into the data. y w w w w The question is: Which straight line fits best? w w x 12

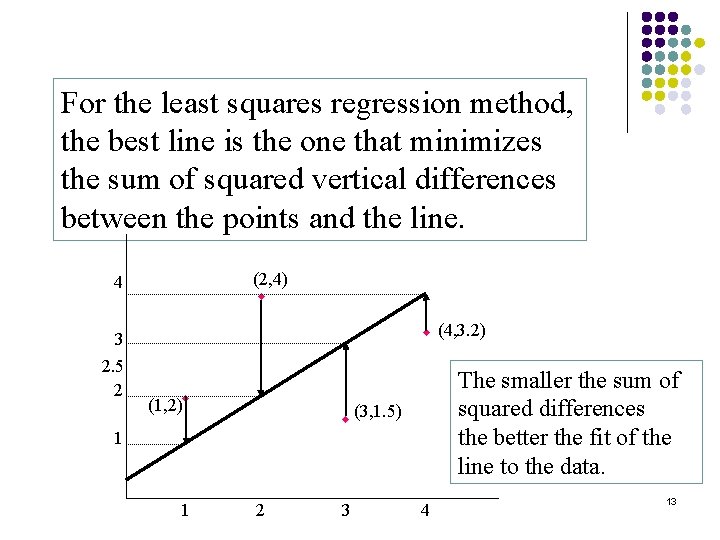
For the least squares regression method, the best line is the one that minimizes the sum of squared vertical differences between the points and the line. (2, 4) w 4 3 2. 5 2 w (4, 3. 2) (1, 2)w w (3, 1. 5) 1 1 The smaller the sum of squared differences the better the fit of the line to the data. 2 3 4 13

14

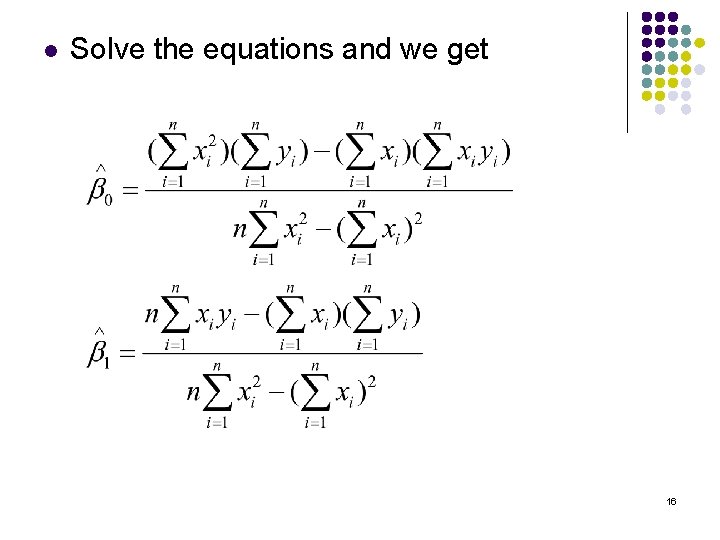
The “best” fitting straight line in the sense of minimizing Q: LS estimate One way to find the LS estimate and Setting these partial derivatives equal to zero and simplifying, we get the normal equations: 15

l Solve the equations and we get 16

l To simplify, we introduce l The resulting equation is known as the least squares regression line, which is an estimate of the true regression line. 17

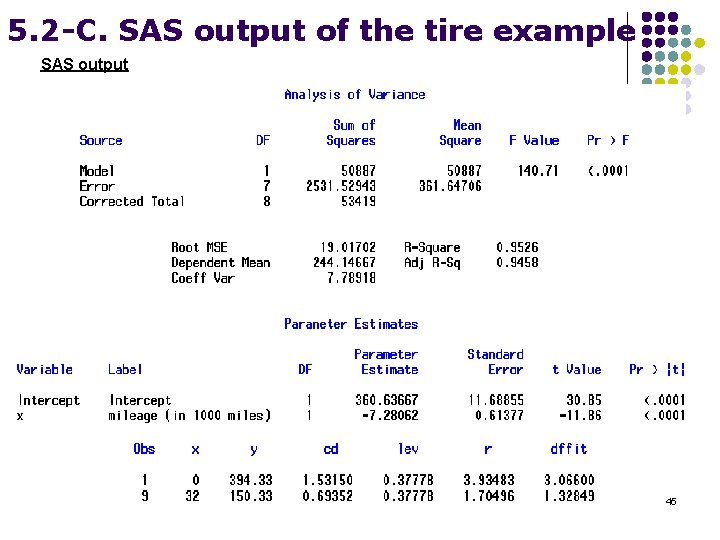
Example 10. 2 (Tire Tread vs. Mileage: LS Line Fit) Find the equation of the line for the tire tread wear data from Table 10. 1, we have and n=9. From these we calculate 18

The slope and intercept estimates are Therefore, the equation of the LS line is Conclusion: there is a loss of 7. 281 mils in the tire groove depth for every 1000 miles of driving. Given a particular We can find This means that the mean groove depth for all tires driven for 25, 000 miles is estimated to be 178. 62 miles. 19

2. 2 Goodness of Fit of the LS Line l Coefficient of Determination and Correlation l The residuals: are used to evaluate the goodness of fit of the LS line. 20

l We define: Note: total sum of squares (SST) Regression sum of squares (SSR) Error sum of squares (SSE) is called the coefficient of determination 21

Example 10. 3 (Tire Tread Wear vs. Mileage: Coefficient of Determination and Correlation l For the tire tread wear data, calculate using the result s from example 10. 2 We have l Next calculate Therefore l The Pearson correlation is where the sign of r follows from the sign of since 95. 3% of the variation in tread wear is accounted for by linear regression on mileage, the relationship between the two is strongly linear with a negative slope. l 22

The Maximum Likelihood Estimators (MLE) l Consider the linear model: where is drawn from a normal population with mean 0 and standard deviation σ, the likelihood function for Y is: l Thus, the log-likelihood for the data is:

The MLE Estimators l Solving l We obtain the MLEs of the three unknown model parameters The MLEs of the model parameters a and b are the same as the LSEs – both unbiased The MLE of the error variance, however, is biased: l l

2. 3 An Unbiased Estimator of s 2 An unbiased estimate of is given by Example 10. 4(Tire Tread Wear Vs. Mileage: Estimate of Find the estimate of for the tread wear data using the results from Example 10. 3 We have SSE=2351. 3 and n-2=7, therefore Which has 7 d. f. The estimate of is miles. 25

3. Statistical Inference on b 0 and b 1 Under the normal error assumption * Point estimators: * Sampling distributions of and : For mathematical derivations, please refer to the Tamhane and Dunlop text book, P 331. 26

Statistical Inference on b 0 and b 1 , Con’t * Pivotal Quantities (P. Q. ’s): * Confidence Intervals (CI’s): 27

Statistical Inference on b 0 and b 1 , Con’t * Hypothesis tests: -- Test statistics: -- At the significance level , we reject in favor of if and only if (iff) -- The first test is used to show whethere is a linear relationship between x and y 28

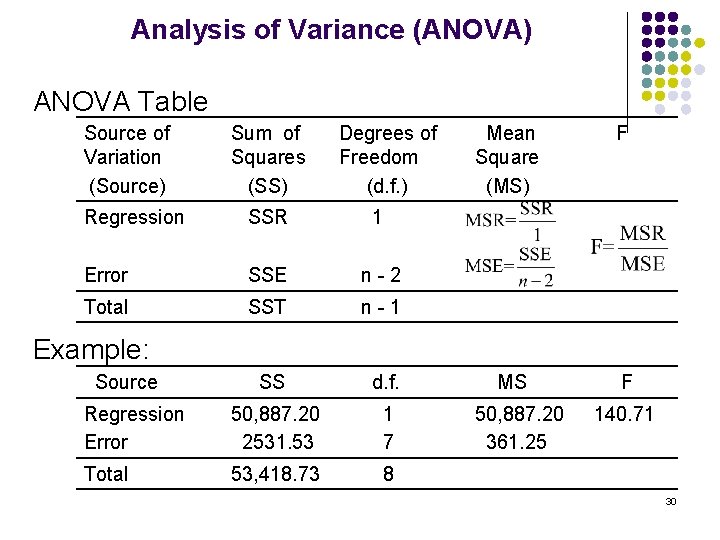
Analysis of Variance (ANOVA), Con’t Mean Square: -- a sum of squares divided by its d. f. 29

Analysis of Variance (ANOVA) ANOVA Table Source of Variation (Source) Sum of Squares (SS) Degrees of Mean F Freedom Square (d. f. ) (MS) Regression Error SSR SSE 1 n - 2 Total SST n - 1 Source SS d. f. Regression Error 50, 887. 20 1 2531. 53 7 Example: Total MS F 50, 887. 20 140. 71 361. 25 53, 418. 73 8 30

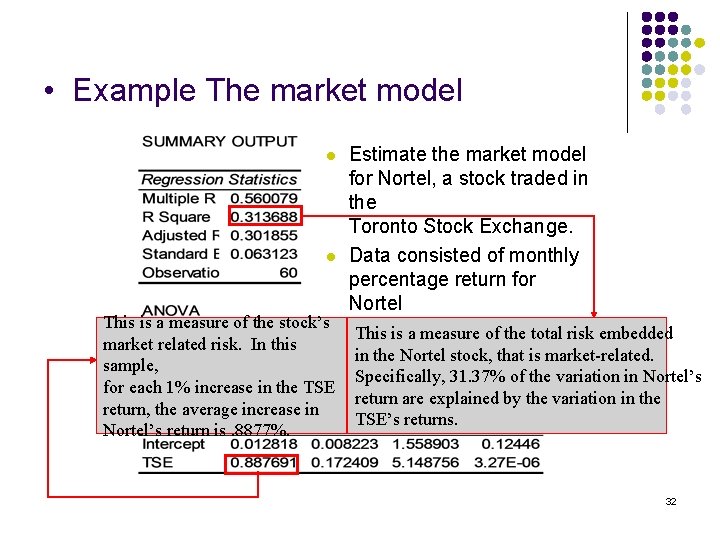
4. Finance Application: Market Model l l One of the most important applications of linear regression is the market model. It is assumed that rate of return on a stock (R) is linearly related to the rate of return on the overall market. R = b 0 + b 1 Rm +e Rate of return on a particular stock Rate of return on some major stock index The beta coefficient measures how sensitive the stock’s rate of return is to changes in the level of the overall market. 31

• Example The market model Estimate the market model for Nortel, a stock traded in the Toronto Stock Exchange. l Data consisted of monthly percentage return for Nortel This is a measure of the stock’s and monthly percentage This is a measure of the total risk embedded market related risk. In this return in the Nortel stock, that is market-related. sample, for all the stocks. Specifically, 31. 37% of the variation in Nortel’s l for each 1% increase in the TSE return, the average increase in Nortel’s return is. 8877%. return are explained by the variation in the TSE’s returns. 32

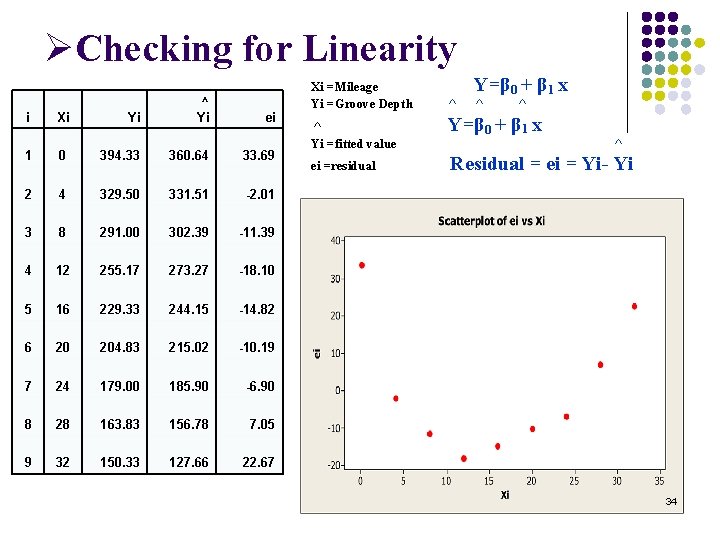
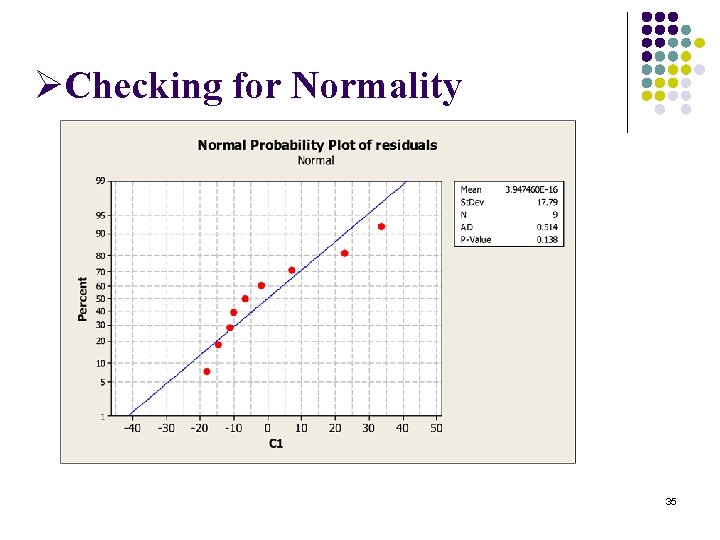
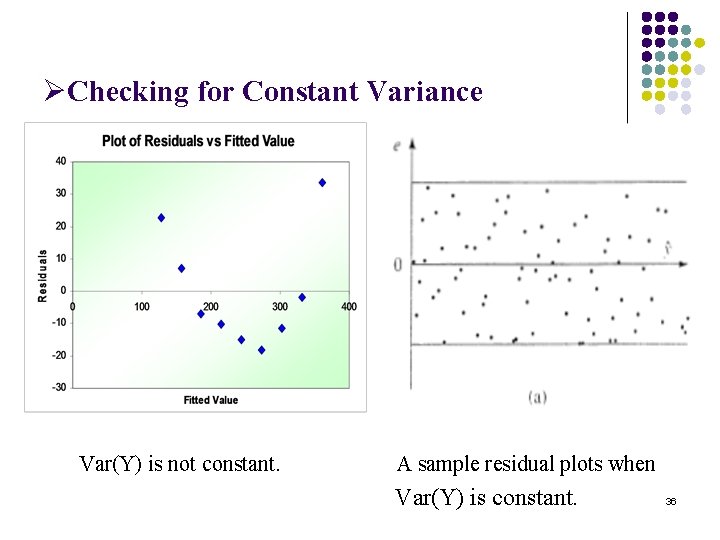
5. Regression Diagnostics 5. 1 Checking for Model Assumptions l l Checking for Linearity Checking for Constant Variance Checking for Normality Checking for Independence 33

ØChecking for Linearity i Xi Yi ^ Yi ei 1 0 394. 33 360. 64 33. 69 2 4 329. 50 331. 51 -2. 01 3 8 291. 00 302. 39 -11. 39 4 12 255. 17 273. 27 -18. 10 5 16 229. 33 244. 15 -14. 82 6 20 204. 83 215. 02 -10. 19 7 24 179. 00 185. 90 -6. 90 8 28 163. 83 156. 78 7. 05 9 32 150. 33 127. 66 22. 67 Xi =Mileage Yi =Groove Depth ^ Y=β 0 + β 1 x ^ ^ ^ Yi =fitted value Y=β 0 + β 1 x ei =residual Residual = ei = Yi- Yi ^ 34

ØChecking for Normality 35

ØChecking for Constant Variance Var(Y) is not constant. A sample residual plots when Var(Y) is constant. 36

ØChecking for Independence l l Does not apply for Simple Linear Regression Model Only apply for time series data 37

5. 2 Checking for Outliers & Influential Observations Ø Ø What is OUTLIER Why checking for outliers is important Mathematical definition How to deal with them 38

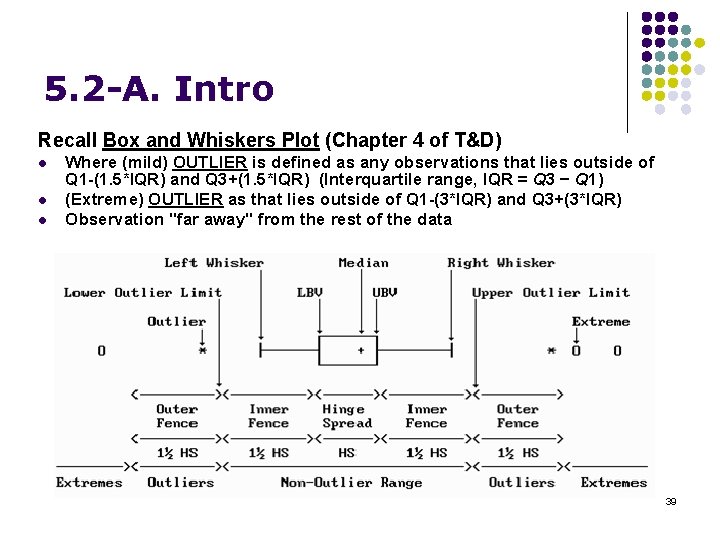
5. 2 -A. Intro Recall Box and Whiskers Plot (Chapter 4 of T&D) l l l Where (mild) OUTLIER is defined as any observations that lies outside of Q 1 -(1. 5*IQR) and Q 3+(1. 5*IQR) (Interquartile range, IQR = Q 3 − Q 1) (Extreme) OUTLIER as that lies outside of Q 1 -(3*IQR) and Q 3+(3*IQR) Observation "far away" from the rest of the data 39

5. 2 -B. Why are outliers a problem? May indicate a sample peculiarity or a data entry error or other problem ; l Regression coefficients estimated that minimize the Sum of Squares for Error (SSE) are very sensitive to outliers >>Bias or distortion of estimates; l Any statistical test based on sample means and variances can be distorted In the presence of outliers >>Distortion of pvalues; l Faulty conclusions. Example: ( Estimators not sensitive to outliers are said to be robust ) l Sorted Data Median Mean Variance 95% CI for mean Real Data 1 3 5 9 12 5 6. 0 20. 6 [0. 45, 11. 55] Data with Error 1 3 5 9 120 5 27. 6 2676. 8 [-36. 630, 91. 83] 40

5. 2 -C. Mathematical Definition Ø Outlier The standardized residual is given by If |ei*|>2, then the corresponding observation may be regarded an outlier. Example: (Tire Tread Wear vs. Mileage) i 1 2 3 4 5 6 7 8 9 ei* 2. 25 -0. 12 -0. 66 -1. 02 -0. 83 -0. 57 -0. 40 0. 43 1. 51 • STUDENTIZED RESIDUAL: a type of standardized residual calculated with the current observation deleted from the analysis. • The LS fit can be excessively influenced by observation that is not necessarily an outlier as defined above. 41

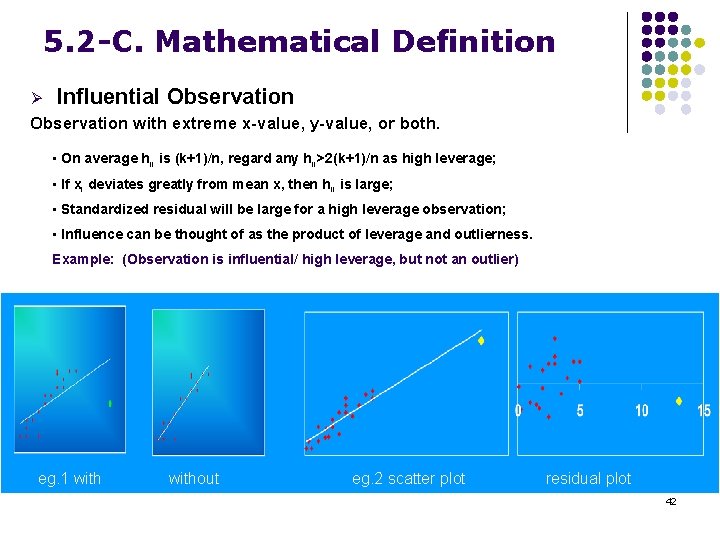
5. 2 -C. Mathematical Definition Ø Influential Observation with extreme x-value, y-value, or both. • On average hii is (k+1)/n, regard any hii>2(k+1)/n as high leverage; • If xi deviates greatly from mean x, then hii is large; • Standardized residual will be large for a high leverage observation; • Influence can be thought of as the product of leverage and outlierness. Example: (Observation is influential/ high leverage, but not an outlier) eg. 1 with without eg. 2 scatter plot residual plot 42

5. 2 -C. SAS code of the tire example SAS code Data cars; Input x y; Datalines; 0 394. 33 4 329. 50 8 291. 00 12 255. 17 16 229. 33 20 204. 83 24 179. 00 28 163. 83 32 150. 33 ; Run; proc reg data=cars; model y=x; output out=resid rstudent=r h=lev cookd=cd dffits=dffit; Run; 43

5. 2 -C. SAS code of the tire example SAS code – continued proc print data=resid; where abs(r)>=2 or lev>(4/9) or cd>(4/9) or abs(dffit)>(2*sqrt(1/9)); run; 44

5. 2 -C. SAS output of the tire example SAS output 45

5. 2 -D. How to deal with Outliers & Influential Observations l l Ø Ø Ø Investigate (Data errors? Rare events? Can be corrected? ) Ways to accommodate outliers Non Parametric Methods (robust to outliers) Data Transformations Deletion (or report model results both with and without the outliers or influential observations to see how much they change) 46

5. 3 Data Transformations Reason l l l To achieve linearity To achieve homogeneity of variance To achieve normality or symmetry about the regression equation 47

Types of Transformation l Linearzing Transformation transformation of a response variable, or predicted variable, or both, which produces an approximate linear relationship between variables. l Variance Stabilizing Transformation make transformation if the constant variance assumption is violated 48

Linearizing Transformation l Use mathematical operation, e. g. square root, power, log, exponential, etc. l Only one variable needs to be transformed in the simple linear regression. Which one? Predictor or Response? Why? 49

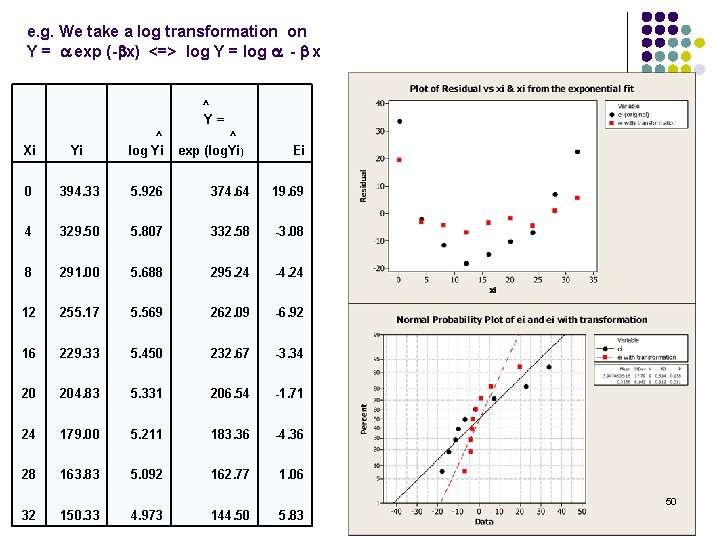
e. g. We take a log transformation on Y = a exp (-bx) <=> log Y = log a - b x ^ Y= Xi Yi ^ log Yi ^ exp (log. Yi) 0 394. 33 5. 926 374. 64 19. 69 4 329. 50 5. 807 332. 58 -3. 08 8 291. 00 5. 688 295. 24 -4. 24 12 255. 17 5. 569 262. 09 -6. 92 16 229. 33 5. 450 232. 67 -3. 34 20 204. 83 5. 331 206. 54 -1. 71 24 179. 00 5. 211 183. 36 -4. 36 28 163. 83 5. 092 162. 77 1. 06 32 150. 33 4. 973 144. 50 5. 83 Ei 50

Variance Stabilizing Transformation Delta method : Two terms Taylor-series approximations Var( h(Y)) ≈ [h(m)]2 g 2 (m) where Var(Y) = g 2(m), E(Y) = m 1. set [h’(m)]2 g 2 (m) = 1 2. h’(m) = 3. h(m) = h(y) = e. g. Var(Y) = c 2 m 2 , where c > 0, g(m) = cm ↔ g(y) = cy h(y) = = = Therefore it is the logarithmic transformation 51

6. Correlation Analysis l Pearson Product Moment Correlation: a measurement of how closely two variables share a linear relationship. l l Useful when it is not possible to determine which variable is the predictor and which is the response. l Health vs wealth. Which is predictor? Which is response? 52

Statistical Inference on the Correlation Coefficient ρ l We can derive a test on the correlation coefficient in the same way that we have been doing in class. l l Assumptions l X, Y are from the bivariate normal distribution Start with point estimator l r: sample correlation coefficient: estimator of the population correlation coefficient ρ l l Get the pivotal quantity l The distribution of r is quite complicated l T 0: test statistic for ρ = 0 l l Do we know everything about the p. q. ? l Yes: T 0 ~ tn-2 under H 0 : ρ=0 53

Bivariate Normal Distribution l pdf: l Properties l l l μ 1, μ 2 means for X, Y σ12, σ22 variances for X, Y ρ the correlation coeff between X, Y 54

Derivation of T 0 Are these equivalent? l Therefore, we can use t as a statistic for testing against the null hypothesis H 0: β 1=0 l Equivalently, we can test against H 0: ρ=0 Substitute After a few steps we can see that these two t-tests are indeed equivalent 55

Exact Statistical Inference on ρ l Test l H 0 : ρ=0 , Ha : ρ≠ 0 l Test statistic: l Example l A researcher wants to determine if two test instruments give similar results. The two test instruments are administered to a sample of 15 students. The correlation coefficient between the two sets of scores is found to be 0. 7. Is this correlation statistically significant at the. 01 level? l H 0 : ρ=0 , Ha : ρ≠ 0 l Reject H 0 iff l for α =. 01, 3. 534 = t 0 > t 13, . 005 = 3. 012 l ▲ Reject H 0 56

Approximate Statistical Inference on ρ l There is no exact method of testing ρ vs an arbitrary ρ0 l l l Distribution of R is very complicated T 0 ~ tn-2 only when ρ = 0 To test ρ vs an arbitrary ρ0 one can use Fisher’s transformation l Therefore, let 57

Approximate Statistical Inference on ρ l Test : l Sample estimate: l Z test statistic: We reject H 0 if |z 0| > zα/2 l CI for ρ: 58

Approximate Statistical Inference on ρ using SAS l Code: l Output: 59

Pitfalls of Regression and Correlation Analysis l Correlation and causation l l Coincidental data l l Sun spots and republicans Lurking variables l l Ticks cause good health Church, suicide, population Restricted range l Local, global linearity 60

7. Simple Linear Regression in Matrix Form n vector of response n → Linear regression model X matrix vector of parameters vector of errors The normal equations: Using matrix notation: Using summations

Matrix Form of Multiple Regression by LS or y=Xb+e LS criterion is: The LS solutions are: in short

Summary Model Assumptions Linear regression analysis Correlation Coefficient ρ and r The Least squares (LS) estimates: b 0 and b 1 Probabilistic model for Linear regression: Correlation Analysis Confidence Interval & Prediction interval Outliers? Influential Observations? Data Transformations? 63

Least Squares (LS) Fit Sample correlation coefficient r Statistical inference on ß 0 & ß 1 Prediction Interval Model Assumptions Linearity Constant Variance Normality Independence Correlation Analysis 64

Homework 5. Due Thursday, 9/24/2015 Please solve the following two questions using SAS 65

Homework 5. Continued 66