Simple Keynesian Model National Income Determination FourSector National

Simple Keynesian Model National Income Determination Four-Sector National Income Model 1

Outline n n n Four-Sector Model Import Function M = f(Y) Export Function X = f (Y) Net Exports X - M Aggregate Expenditure Function E = f(Y) Output-Expenditure Approach: Equilibrium National Income Ye 2

Outline n n n Factors affecting Ye Expenditure Multipliers k E Tax Multipliers k T Balanced-Budget Multipliers k B Injection-Withdrawal Approach: Equilibrium National Income Ye 3

Four-Sector Model n n With the introduction of the foreign sector (i. e. w/ households C, firms I, government expenditure G) aggregate expenditure E consists of one more component, net exports X- M. E = C + I + G + (X - M) Still, the equilibrium condition is Planned Y = Planned E 4

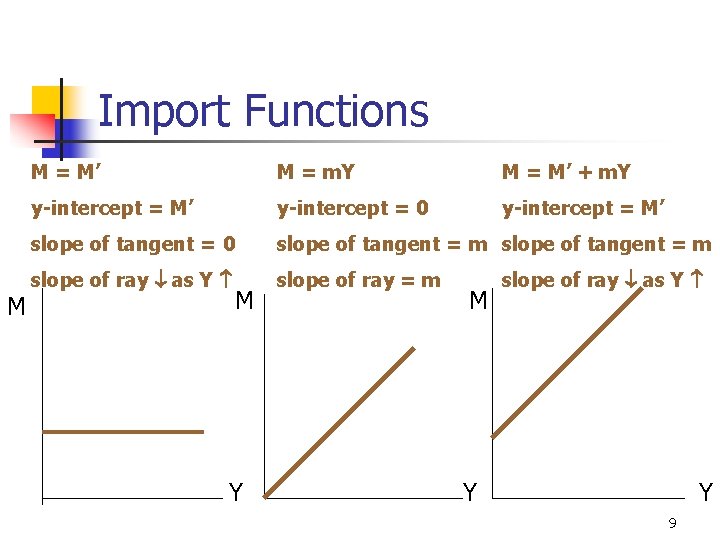
Import Function n n n Imports M is usually assumed to be a function of national income Y. M = M’ M = m. Y M = M’ + m. Y M and Y are assumed to be positively correlated. M = M’ + m. Y is the typical form being used 5

Import Function n Autonomous Imports M’ this is the y-intercept of the import function M’ is an exogenous variable, i. e. , independent of the income level Y and is determined by forces outside the simple Keynesian 4 -sector model 6

Import Function n n n Marginal Propensity to Import MPM = m this is defined as the change in imports per unit change in income Y, i. e. , m = M / Y it is the slope of tangent of the import function it is usually assumed to be a constant m = 0 or m is a +ve number MPM is also an exogenous variable 7

Import Function n n Average Propensity to Import APM it is the ratio of total imports to total income, i. e. , APM = M / Y it is the slope of ray of the import function APM when Y except M = m. Y when MPM = APM = m 8

Import Functions M M = M’ M = m. Y M = M’ + m. Y y-intercept = M’ y-intercept = 0 y-intercept = M’ slope of tangent = 0 slope of tangent = m slope of ray as Y slope of ray = m M Y M slope of ray as Y Y Y 9

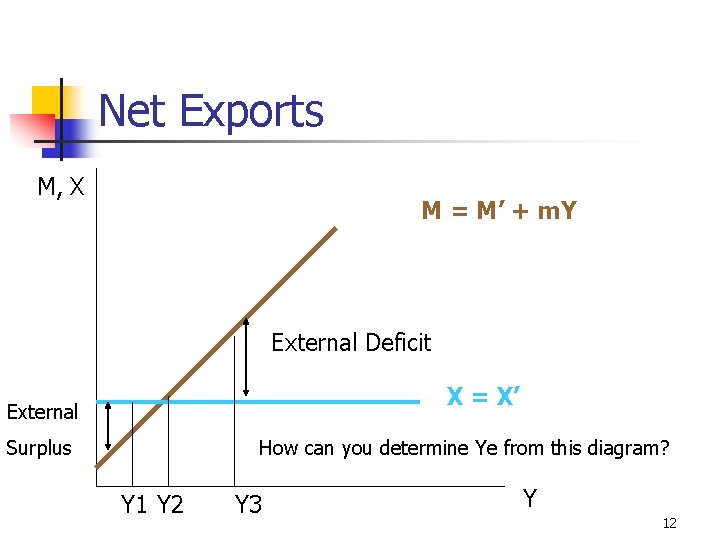
Export Function n n X = f (Y) this is a relationship between the amount of exports X and national income Y it is usually assumed to be an exogenous function X = X’ We always consider the amount of net exports, i. e. , X - M Net exports = X - M = X’ - M’ - m. Y 10

Net Exports n n When net exports is positive, i. e. , when X > M, the external sector BOP is in surplus When net exports is negative, i. e. , when X < M, the external sector BOP is in deficit When net exports is zero, i. e. , when X = M, the external sector BOP is in balance {Trade deficit/surplus v. s. Budget deficit/surplus} 11

Net Exports M, X M = M’ + m. Y External Deficit X = X’ External Surplus How can you determine Ye from this diagram? Y 1 Y 2 Y 3 Y 12

Aggregate Expenditure Function n E = C + I + G + (X - M) n n n n C = C’ + c. Yd T = T’ + t. Y I = I’ G = G’ X = X’ M = M’ + m. Y E= 13

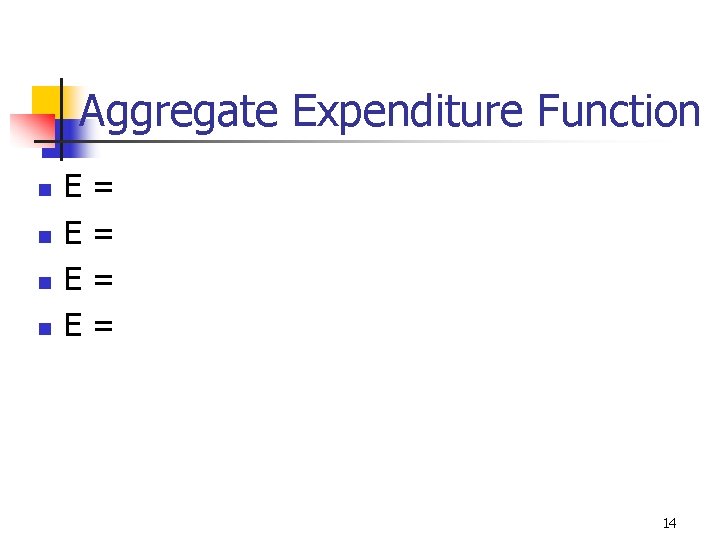
Aggregate Expenditure Function n n E E = = 14

Output-Expenditure Approach n In equilibrium Y = E Y= ( )Y = Y= n Y = k E * E’ n n n k. E= E’ = 15

Factors affecting Ye n n n Change in E’ If X’ E If M’ E Y Y Change in slope of tangent of E / k E If m c-ct- m E steeper Y 16

Import Multiplier k n n M It is the ratio of change in national income Y to a change in autonomous import M’ -1 Y = M’ 1 - c - m + ct 17

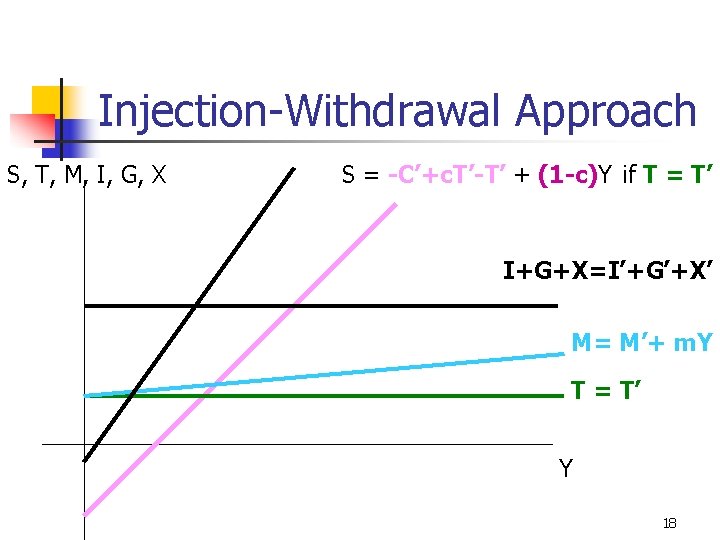
Injection-Withdrawal Approach S, T, M, I, G, X S = -C’+c. T’-T’ + (1 -c)Y if T = T’ I+G+X=I’+G’+X’ M= M’+ m. Y T = T’ Y 18