Simple Interest Objective Use the simple interest formula

Simple Interest Objective: Use the simple interest formula.

If someone borrows money, what factors influence how much is paid back? Principal -How much was borrowed. Time - How long it was borrowed for. (in years) Rate - What interest was charged. (annual % rate) Amount to Payback = Principal + Interest = Principal Rate Time

Joe borrows $200 from the bank at 6% simple interest for 3 years. What interest does he owe, and what is his total balance (amount to payback) Interest Balance = P + I Balance = 200 + 36 Balance = 236 Balance = $236

Juan invests $5000 in bonds for 6 months at an annual interest rate of 7%. How much interest did he earn, and what is the balance in his account Interest Balance = P + I Balance = 5000 + 175 Balance = 5175 Balance = $5175

Find the simple interest and the balance. Balance = P + I Balance = 2000 + 60 Balance = $2060

Find the annual simple interest rate.

Find the annual simple interest rate.

Find the principal amount invested.
Quick Draw for Points • You will have 60 seconds to solve each problem • The text is Simple Interest Problems

Example 1: Finding Interest on a Loan To buy a car, Jessica borrowed $15, 000 for 3 years at an annual simple interest rate of 9%. How much interest will she pay if she pays the entire loan off at the end of the third year? First, find the interest she will pay. I=P r t I = 15, 000 I = 4050 Use the formula. 0. 09 3 Substitute. Use 0. 09 for 9%. Solve for I.

Example 1 A: Finding Total Payment on a Loan What is the total amount that she will repay? You can find the total amount A to be repaid on a loan by adding the principal P to the interest I. Jessica will pay $4050 in interest. P+I=A 15, 000 + 4050 = A 19, 050 = A principal + interest = total amount Substitute. Solve for A. Jessica will repay a total of $19, 050 on her loan.

Example 2 TJ invested $4000 in a bond at a yearly rate of 2%. He earned $200 in interest. How long was the money invested? I=P r 200 = 4000 200 = 80 t 2. 5 = t t 0. 02 Use the formula. t Substitute values into the equation. Solve for t. The money was invested for 2. 5 years, or 2 years and 6 months.

Example 3 Bertha deposited $1000 into a retirement account when she was 18. How much will Bertha have in this account after 50 years at a yearly simple interest rate of 7. 5%? I=P r I = 1000 I = 3750 t 0. 075 Use the formula. 50 Substitute. Use 0. 075 for 7. 5%. Solve for I. The interest is $3750. Now you can find the total.

Example 3 Continued P+I=A Use the formula. 1000 + 3750 = A Substitute. 4750 = A Solve for A. Bertha will have $4750 in the account after 50 years.

Example 4 Mr. Mogi borrowed $9000 for 10 years to make home improvements. If he repaid a total of $20, 000 at what interest rate did he borrow the money? P+I=A Use the formula. 9000 + I = 20, 000 Substitute. I = 20, 000 – 9000 = 11, 000 Subtract 9000 from both sides. He paid $11, 000 in interest. Use the amount of interest to find the interest rate.
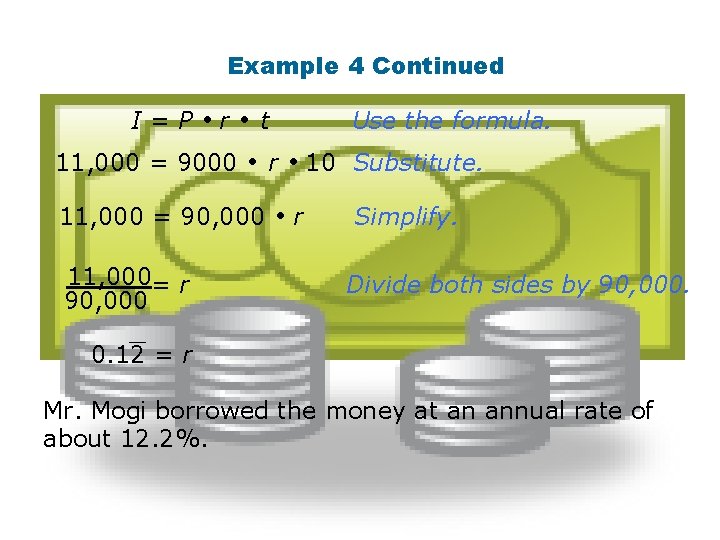
Example 4 Continued I=P r 11, 000 = 9000 t 11, 000 = 90, 000 11, 000= r 90, 000 Use the formula. r r 10 Substitute. Simplify. Divide both sides by 90, 000. 0. 12 = r Mr. Mogi borrowed the money at an annual rate of about 12. 2%.

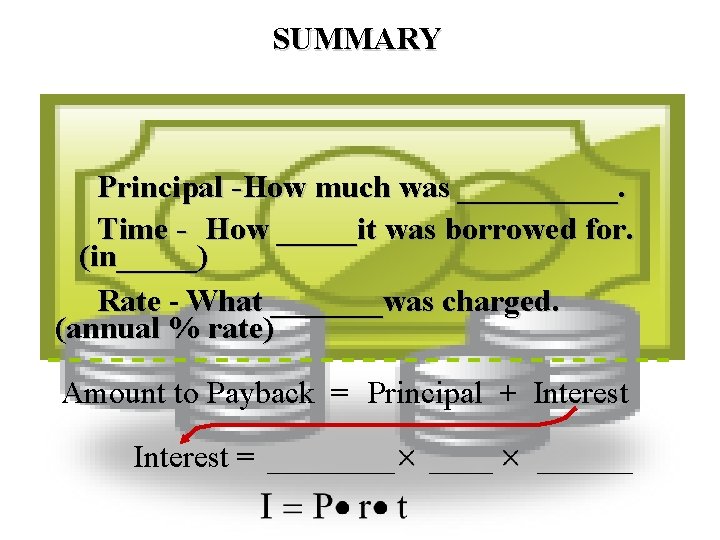
SUMMARY Principal -How much was _____. Time - How _____it was borrowed for. (in_____) Rate - What _______was charged. (annual % rate) Amount to Payback = Principal + Interest = ______
- Slides: 18