Simple Harmonic Motion V Circular Motion The Simple

Simple Harmonic Motion (V) Circular Motion The Simple Pendulum Physics 1 D 03 - Lecture 34 1

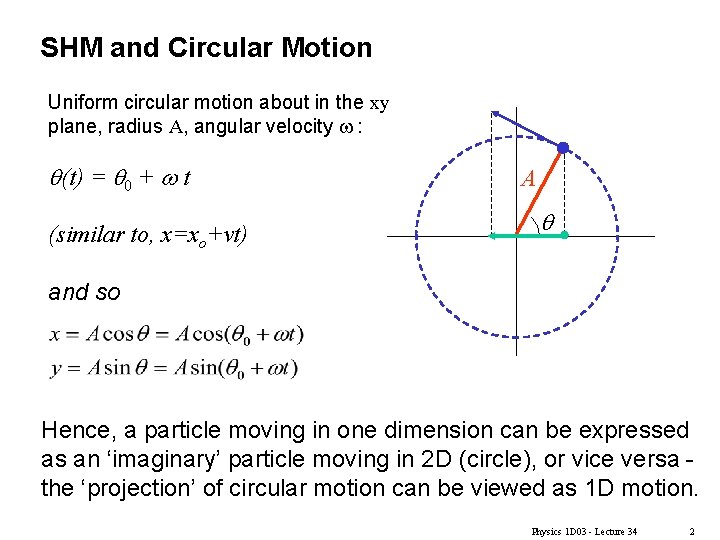
SHM and Circular Motion Uniform circular motion about in the xy plane, radius A, angular velocity w : q(t) = q 0 + w t (similar to, x=xo+vt) A q and so Hence, a particle moving in one dimension can be expressed as an ‘imaginary’ particle moving in 2 D (circle), or vice versa the ‘projection’ of circular motion can be viewed as 1 D motion. Physics 1 D 03 - Lecture 34 2

Compare with our expression for 1 -D SHM. Result: SHM is the 1 -D projection of uniform circular motion. Physics 1 D 03 - Lecture 34 3

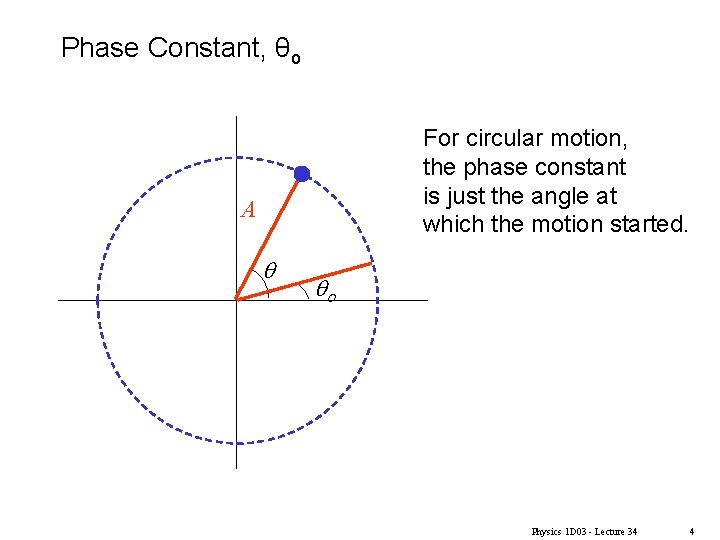
Phase Constant, θo For circular motion, the phase constant is just the angle at which the motion started. A q qo Physics 1 D 03 - Lecture 34 4

Example An object is moving in circular motion with an angular frequency of 3π rad/s, and starts with an initial angle of π/6. If the amplitude is 2. 0 m, what is the objects angular position at t=3 sec ? What are the x and y values of the position at this time ? Physics 1 D 03 - Lecture 34 5

Simple Pendulum Gravity is the “restoring force” taking the place of the “spring” in our block/spring system. L Instead of x, measure the displacement as the arc length s along the circular path. θ T Write down the tangential component of F=ma: mg Restoring force s mg sin θ Physics 1 D 03 - Lecture 34 6

Simple Pendulum Using sin(θ)~θ for small angles, we have the following equation of motion: L θ T Which give us: ------------------------------------- mg Hence: or: Application - measuring height - finding variations in g → underground resources Physics 1 D 03 - Lecture 34 7

Actually: SHM: Simple pendulum: The pendulum is not a simple harmonic oscillator! However, take small oscillations: (radians) if q is small. Then Physics 1 D 03 - Lecture 34 8

For small q : This looks like , with angle q instead of x. The pendulum oscillates in SHM with an angular frequency and the position is given by phase constant amplitude (2 p / period) Physics 1 D 03 - Lecture 34 9

Question: A geologist is camped on top of a large deposit of nickel ore, in a location where the gravitational field is 0. 01% stronger than normal. the period of his pendulum will be a) longer b) shorter (and by how much, in percent? ) Physics 1 D 03 - Lecture 34 10

Application Pendulum clocks (“grandfather clocks”) often have a swinging arm with an adjustable weight. Suppose the arm oscillates with T=1. 05 sec and you want to adjust it to 1. 00 sec. Which way do you move the weight? ? Physics 1 D 03 - Lecture 34 11

Question: A simple pendulum hangs from the ceiling of an elevator. If the elevator accelerates upwards, the period of the pendulum: a) Gets shorter b) Gets larger c) Stays the same Question: What happens to the period of a simple pendulum if the mass m is doubled? Physics 1 D 03 - Lecture 34 12

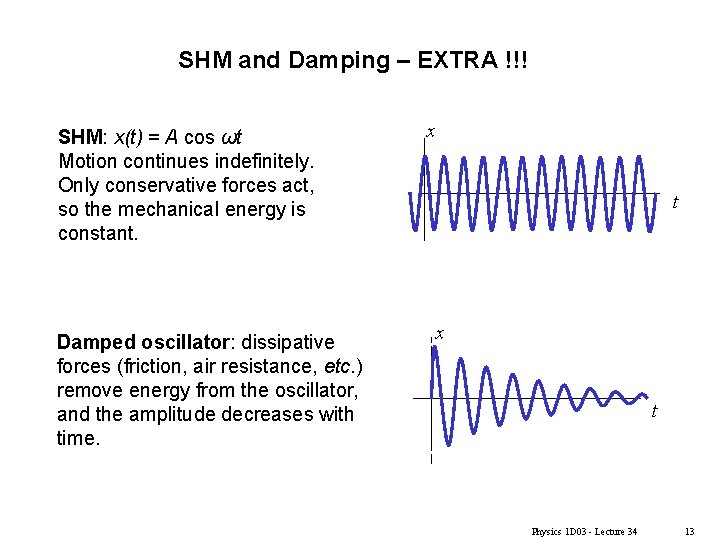
SHM and Damping – EXTRA !!! SHM: x(t) = A cos ωt Motion continues indefinitely. Only conservative forces act, so the mechanical energy is constant. Damped oscillator: dissipative forces (friction, air resistance, etc. ) remove energy from the oscillator, and the amplitude decreases with time. x t Physics 1 D 03 - Lecture 34 13

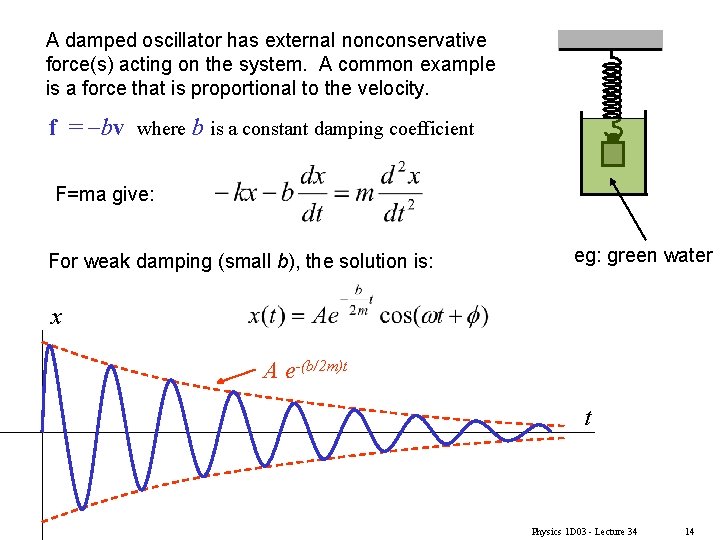
A damped oscillator has external nonconservative force(s) acting on the system. A common example is a force that is proportional to the velocity. f = -bv where b is a constant damping coefficient F=ma give: For weak damping (small b), the solution is: eg: green water x A e-(b/2 m)t t Physics 1 D 03 - Lecture 34 14