Simple Harmonic Motion Oscillatory Systems Periodic motion Elasticity





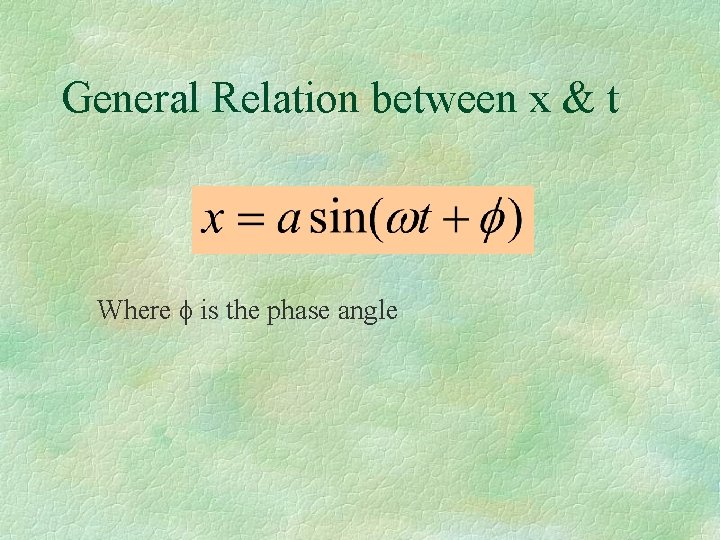










- Slides: 33

Simple Harmonic Motion

Oscillatory Systems § § § Periodic motion Elasticity Inertia Interchange of energies Examples: l l Mass on helical spring Cantilever Simple pendulum Vertical rod floating in liquid

Characteristics of SHM § Occurs in many systems § Isochronous oscillation § Possesses springiness (elasticity) to store P. E. § Possesses inertia to store K. E. § Period of vibration depends on elastic and inertia factors § Constant total energy

§ Conditions for performing SHM l l l acceleration is always directed towards a fixed point acceleration varies directly as its distance from the fixed point i. e. in linear motion in angular motion

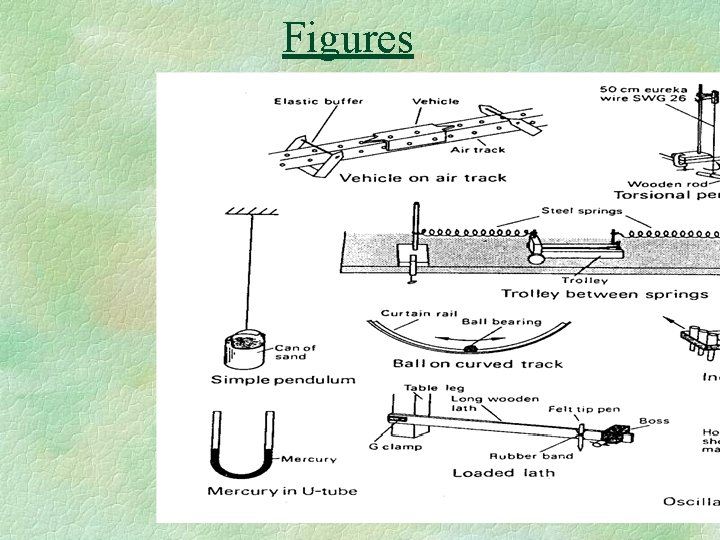
Figures

Terms of Reference § Amplitude § Period § Frequency l unit: Hertz

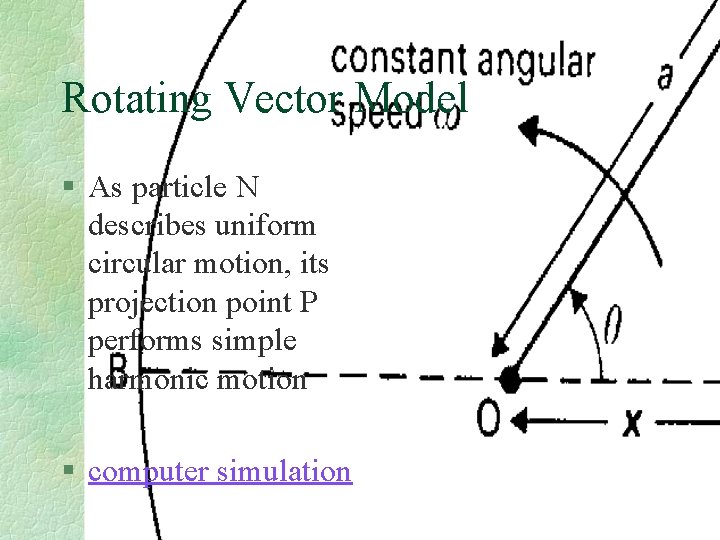
Rotating Vector Model § As particle N describes uniform circular motion, its projection point P performs simple harmonic motion § computer simulation

Kinematics of SHM § Displacement: x = a cos t § Velocity: § Acceleration:

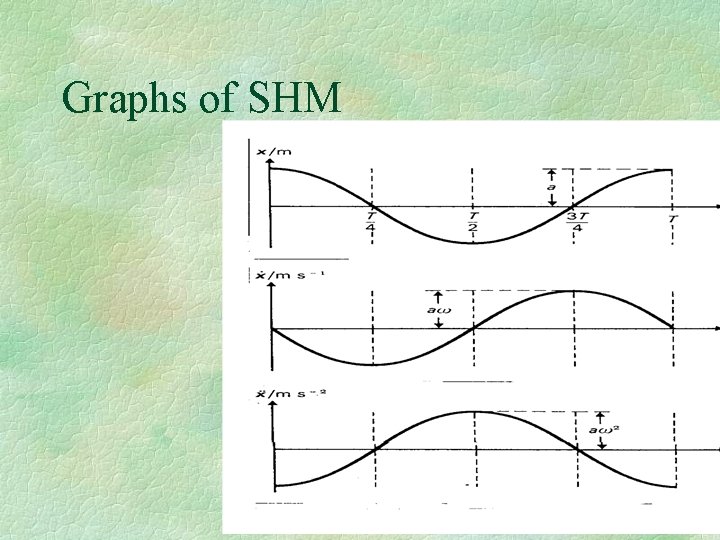
Graphs of SHM
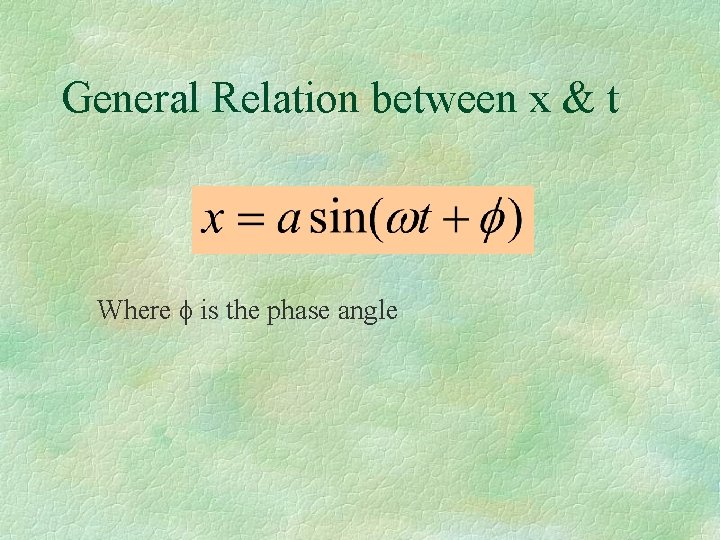
General Relation between x & t Where is the phase angle

Experimental Verification of the relationship • Experimental set up:

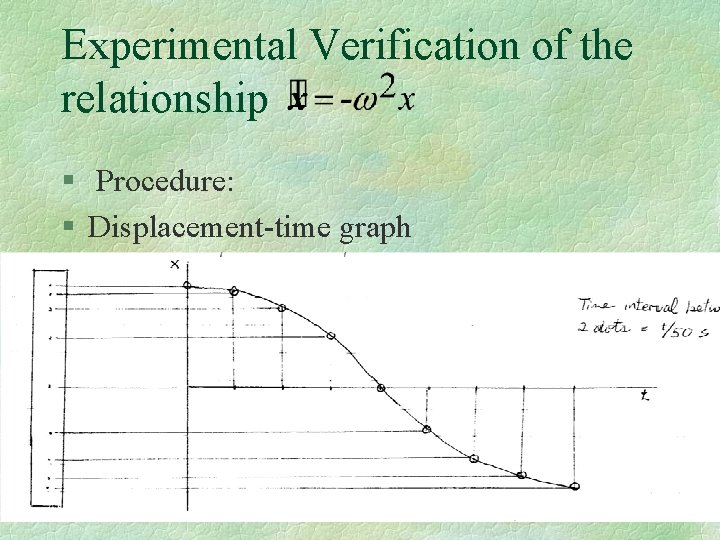
Experimental Verification of the relationship § Procedure: § Displacement-time graph

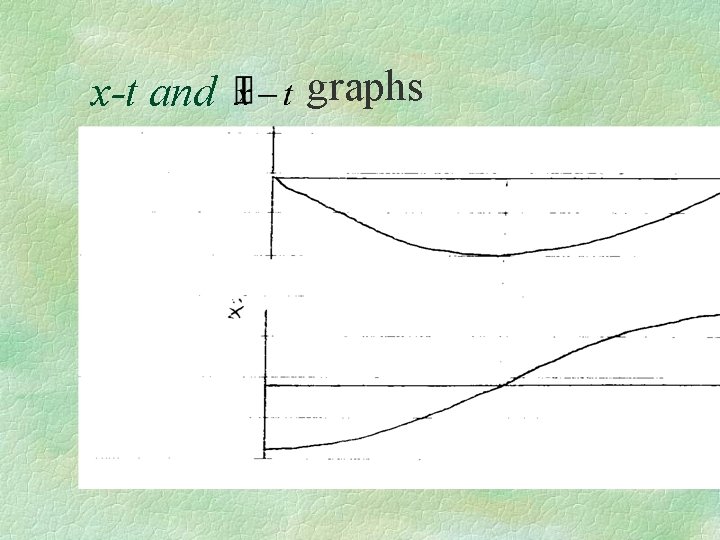
x-t and graphs

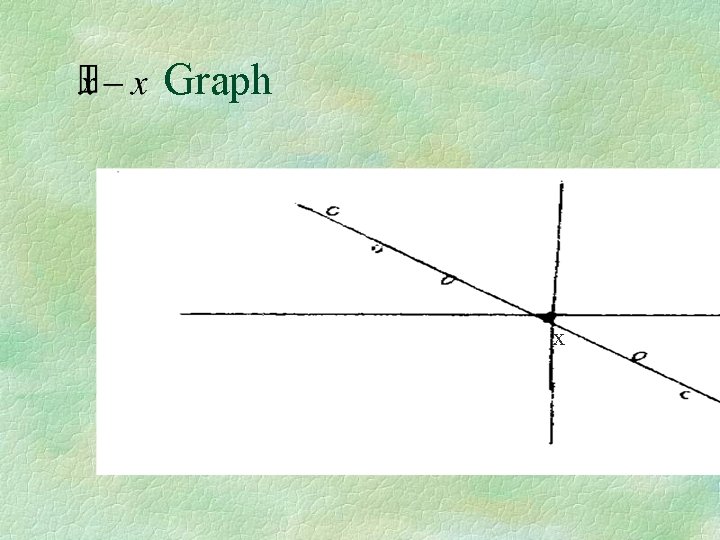
Graph x

Solving Problems on SHM § Assume displacement x from the mean position § Draw a diagram showing all forces § Apply Newton’s second law with appropriate sign convention § Show that § The constant of proportionality = 2 § Period T = 2 /

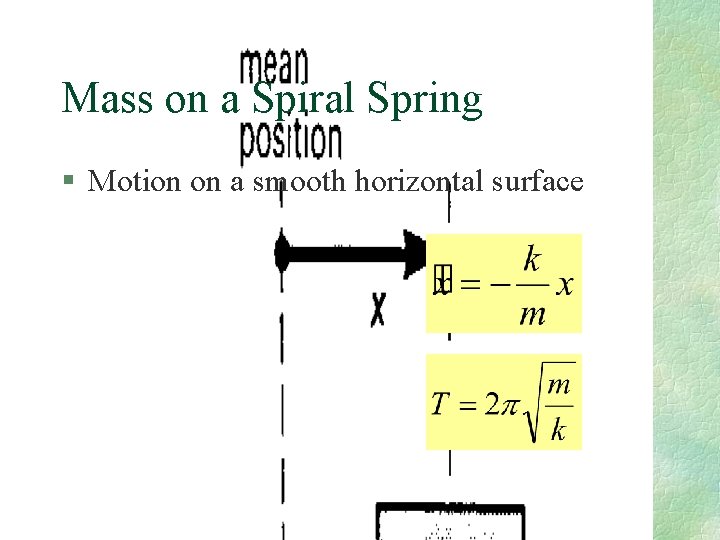
Mass on a Spiral Spring § Motion on a smooth horizontal surface

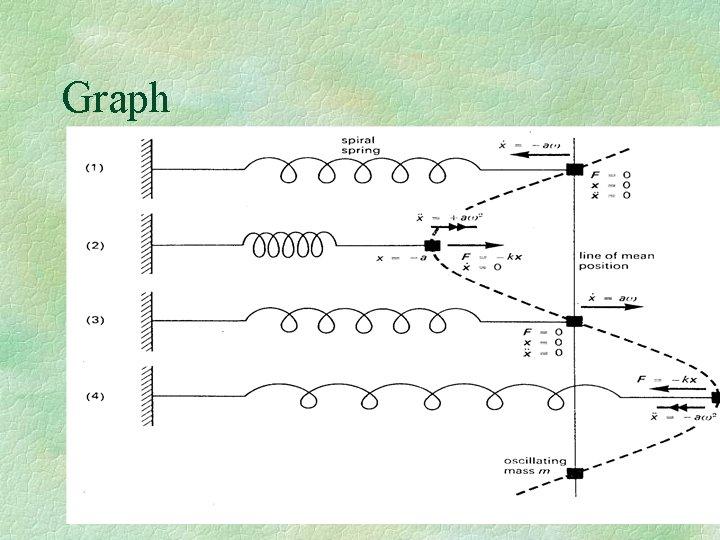
Graph

§ Motion under gravity

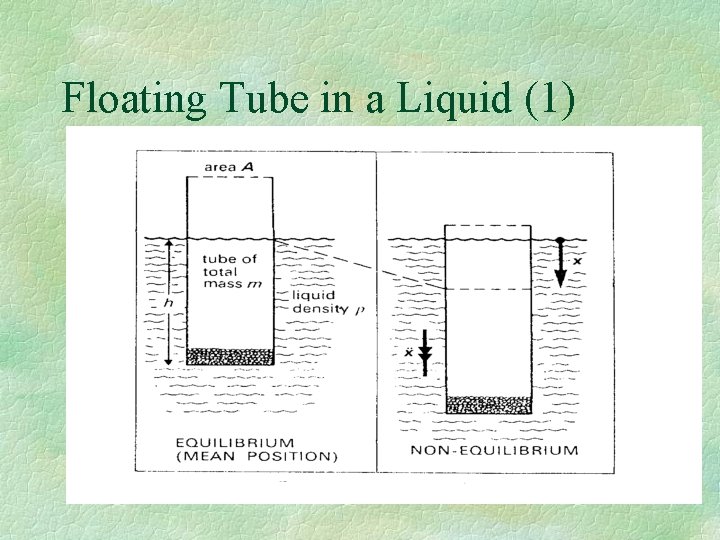
Floating Tube in a Liquid (1)

Floating Tube in a Liquid (2) Effects of viscosity of liquid: • causes damping • takes away K. E. from the oscillating tube

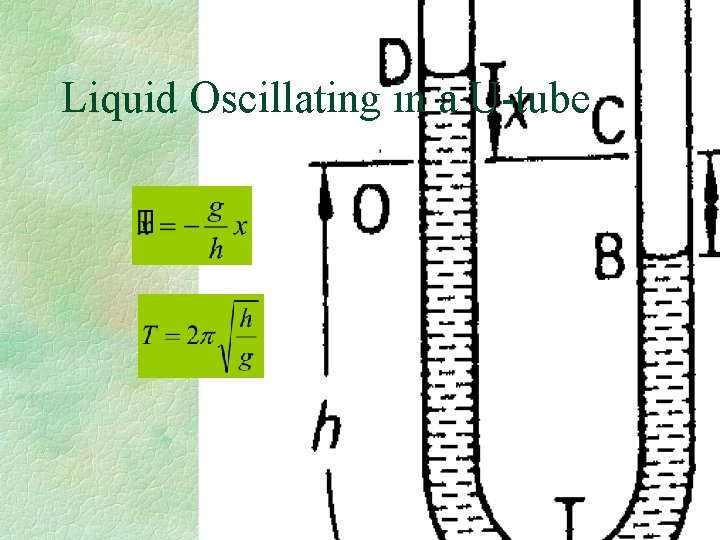
Liquid Oscillating in a U-tube

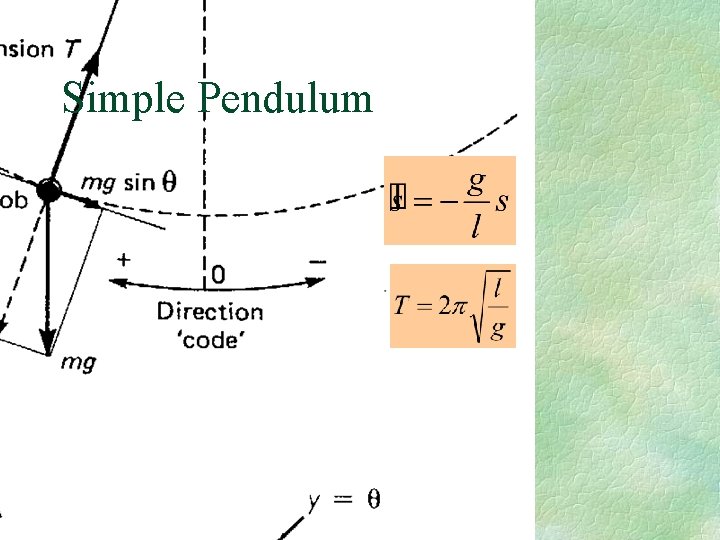
Simple Pendulum

Arrangement of Springs (1) K = equivalent spring constant

Arrangement of Springs (2) § Springs connected in series:

Arrangement of Springs (3) § Springs connected in parallel:

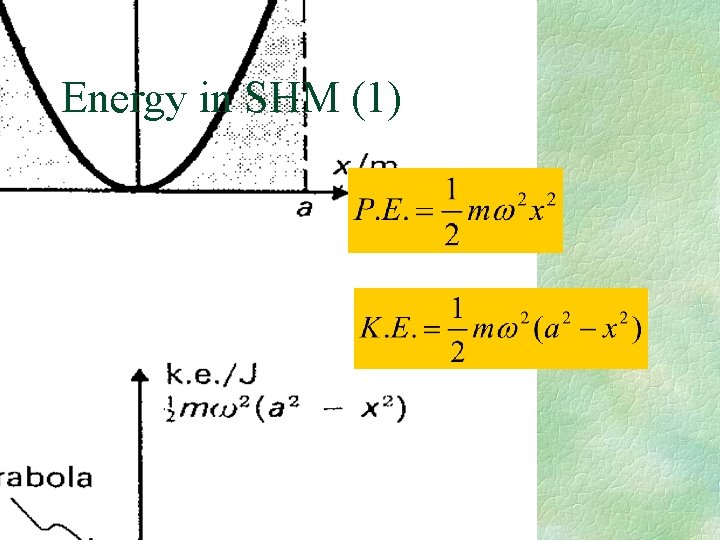
Energy in SHM (1)

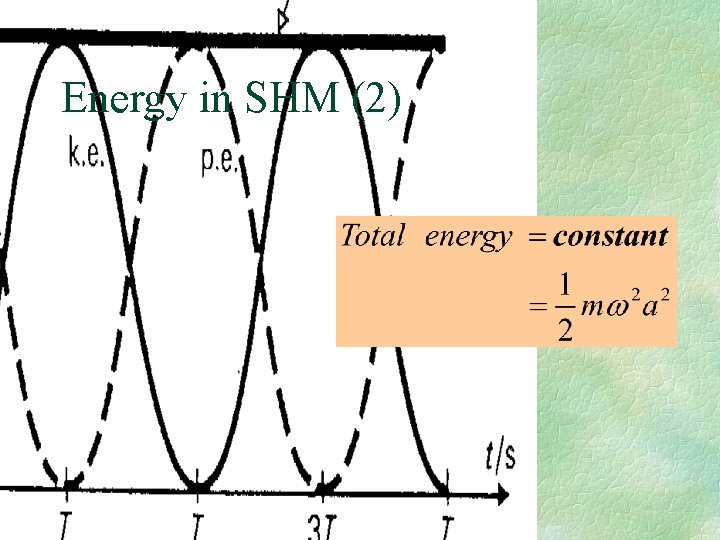
Energy in SHM (2)

Phase Difference § § Phase leading Phase lagging In phase Out of phase (Antiphase)

Superposition of Two Harmonic Variations § The amplitude and phase of the resultant is obtained by the parallelogram law

Experimental Determination of g (1) § a) A simple pendulum: • Plot a graph of T 2 vs l • Slope =

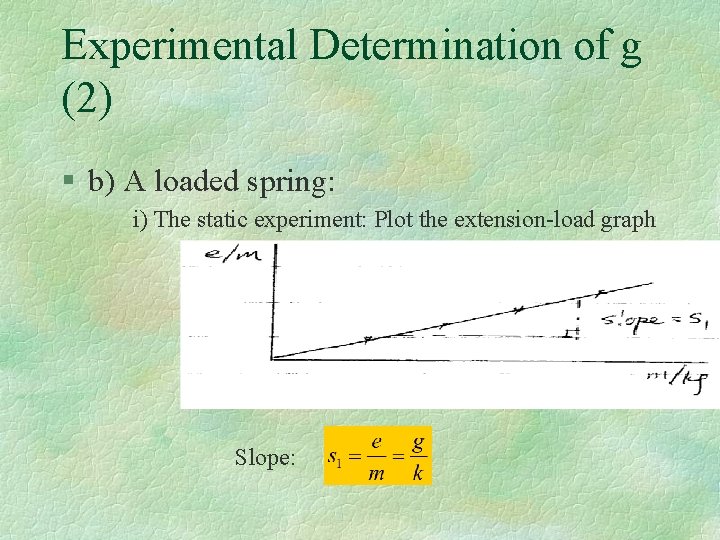
Experimental Determination of g (2) § b) A loaded spring: i) The static experiment: Plot the extension-load graph Slope:

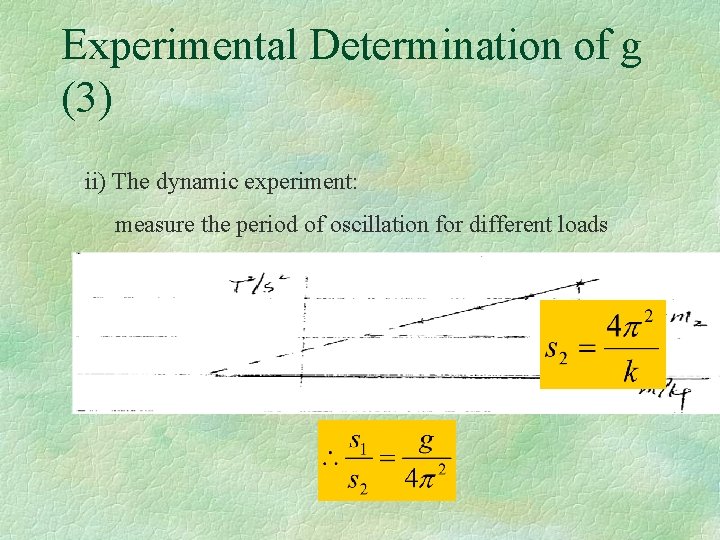
Experimental Determination of g (3) ii) The dynamic experiment: measure the period of oscillation for different loads

EXAMPLES