SIMPLE HARMONIC MOTION NEWTONS LAW simple not simple

SIMPLE HARMONIC MOTION: NEWTON’S LAW simple not simple PRIOR READING: Main 1. 1, 2. 1 Taylor 5. 1, 5. 2 0 http: //www. myoops. org/twocw/mit/NR/rdonlyres/Physics/8 -012 Fall-2005/7 CCE 46 AC-405 D-4652 -A 724 -64 F 831 E 70388/0/chp_physi_pndulm. jpg

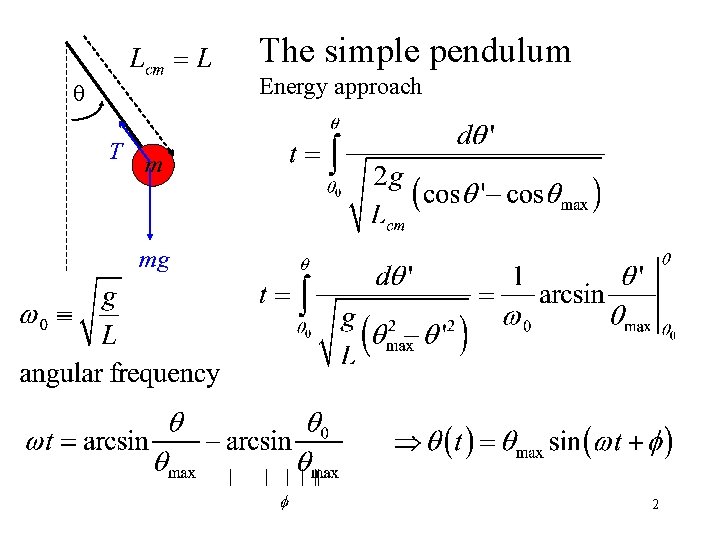
The simple pendulum Energy approach q T m mg 1

The simple pendulum Energy approach q T m mg 2

The simple pendulum q T m Newton Known torque mg This is NOT a restoring force proportional to displacement (Hooke’s law motion) in general, but IF we consider small motion, IT IS! Expand the sin series … 3

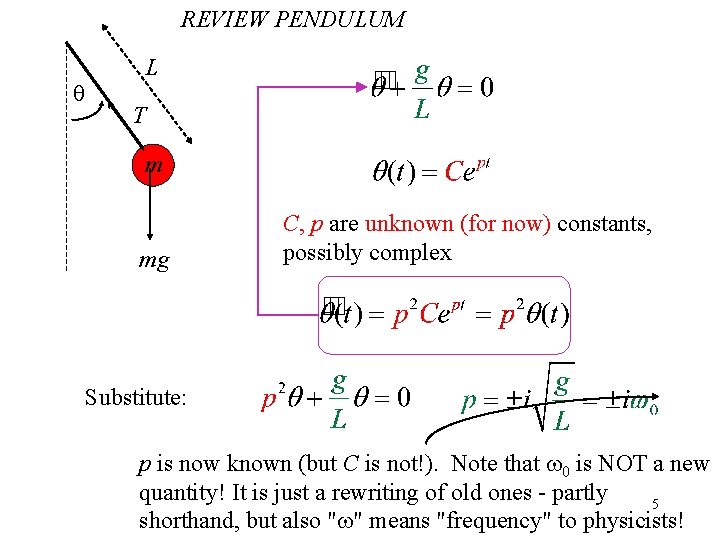
q L The simple pendulum in the limit of small angular displacements T m mg What is (t) such that the above equation is obeyed? is a variable that describes position t is a parameter that describes time "dot" and "double dot" mean differentiate w. r. t. time g, L are known constants, determined by the system. 4

REVIEW PENDULUM q L T m mg C, p are unknown (for now) constants, possibly complex Substitute: p is now known (but C is not!). Note that w 0 is NOT a new quantity! It is just a rewriting of old ones - partly 5 shorthand, but also "w" means "frequency" to physicists!

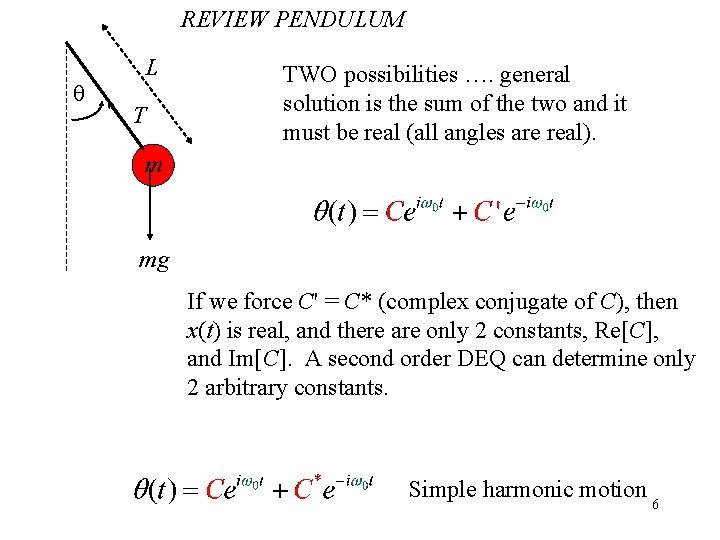
REVIEW PENDULUM q L T TWO possibilities …. general solution is the sum of the two and it must be real (all angles are real). m mg If we force C' = C* (complex conjugate of C), then x(t) is real, and there are only 2 constants, Re[C], and Im[C]. A second order DEQ can determine only 2 arbitrary constants. Simple harmonic motion 6

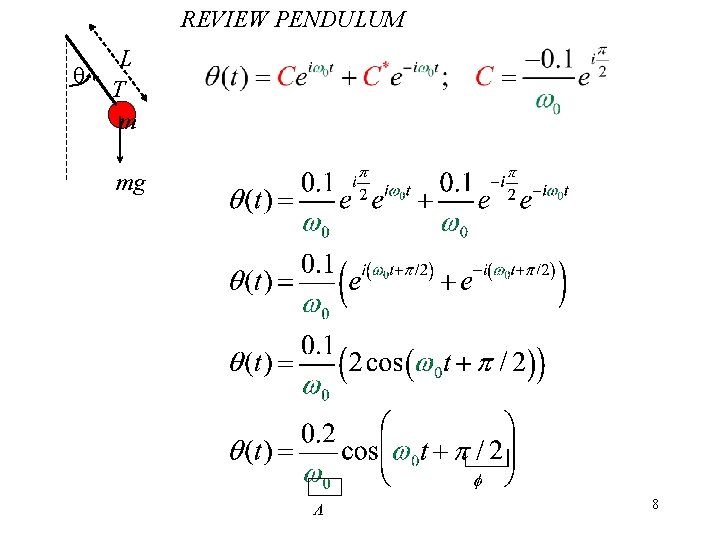
REVIEW PENDULUM q L T m mg Re[C], Im[C] chosen to fit initial conditions. Example: q(0) = 0 rad and dqdt(0) = 0. 2 rad/sec 7

REVIEW PENDULUM q L T m mg 8

Remember, all these are equivalent forms. All of them have a known w 0=(g/L)1/2, and all have 2 more undetermined constants that we find … how? Do you remember how the A, B, C, D constants are related? If not, go back and review until it becomes second nature! 9

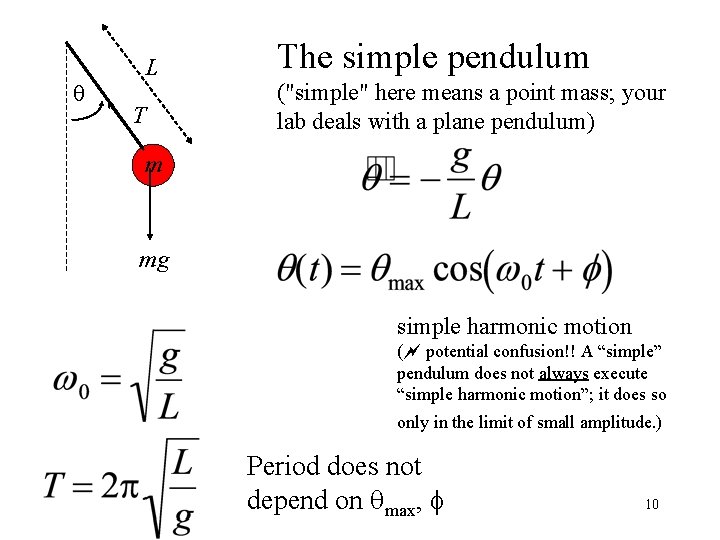
q L T The simple pendulum ("simple" here means a point mass; your lab deals with a plane pendulum) m mg simple harmonic motion ( potential confusion!! A “simple” pendulum does not always execute “simple harmonic motion”; it does so only in the limit of small amplitude. ) Period does not depend on qmax, f 10

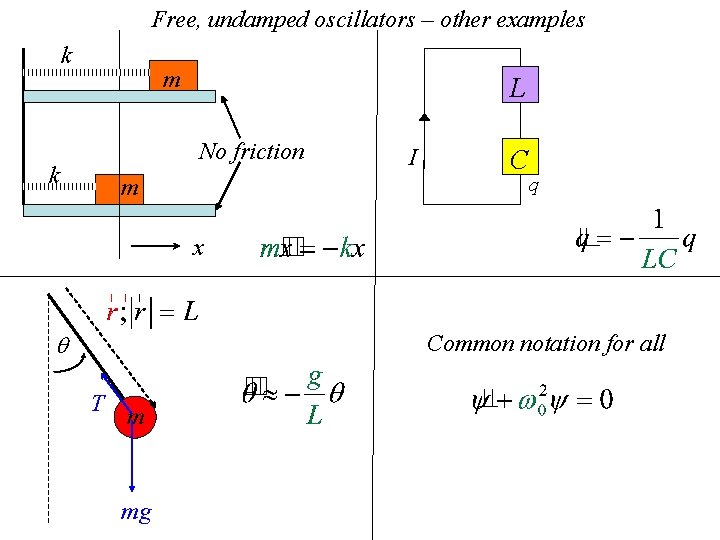
Free, undamped oscillators – other examples k m L No friction k m I C q x Common notation for all T m mg

• The following slides simply repeat the previous discussion, but now for a mass on a spring, and for a series LC circuit 12

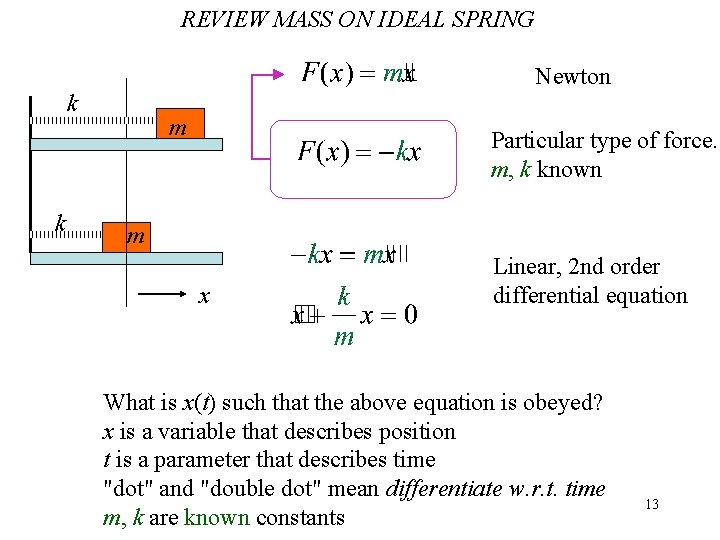
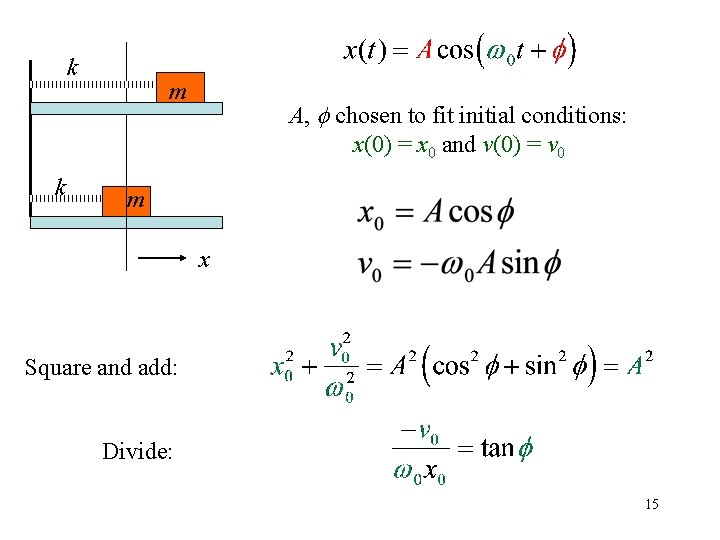
REVIEW MASS ON IDEAL SPRING Newton k k m Particular type of force. m, k known m x Linear, 2 nd order differential equation What is x(t) such that the above equation is obeyed? x is a variable that describes position t is a parameter that describes time "dot" and "double dot" mean differentiate w. r. t. time m, k are known constants 13

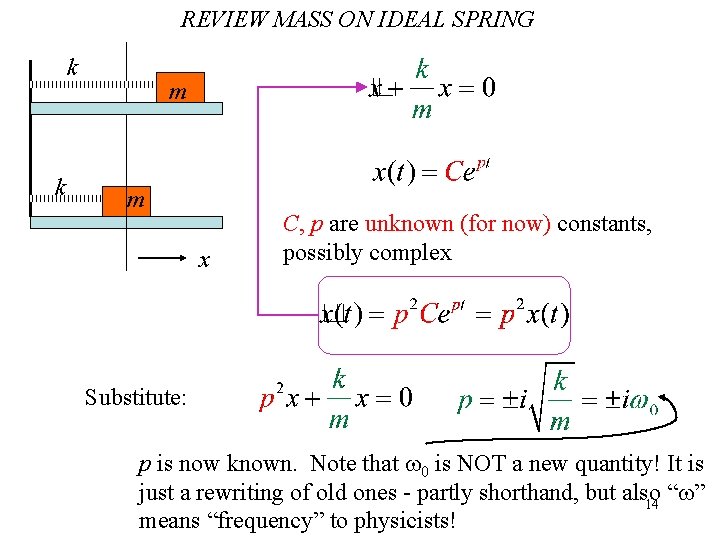
REVIEW MASS ON IDEAL SPRING k k m m x C, p are unknown (for now) constants, possibly complex Substitute: p is now known. Note that w 0 is NOT a new quantity! It is just a rewriting of old ones - partly shorthand, but also “w” 14 means “frequency” to physicists!

k k m A, f chosen to fit initial conditions: x(0) = x 0 and v(0) = v 0 m x Square and add: Divide: 15

2 arbitrary constants (A, f) because 2 nd order linear differential equation 16

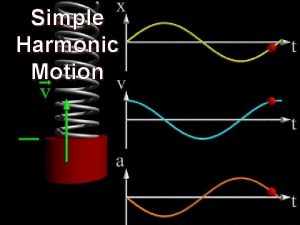
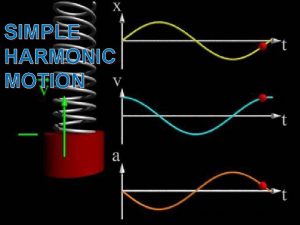
Position: • A, f are unknown constants - must be determined from initial conditions • w 0, in principle, is known and is a characteristic of the physical system Velocity: Acceleration: This type of pure sinusoidal motion with a single frequency is called SIMPLE HARMONIC MOTION 17

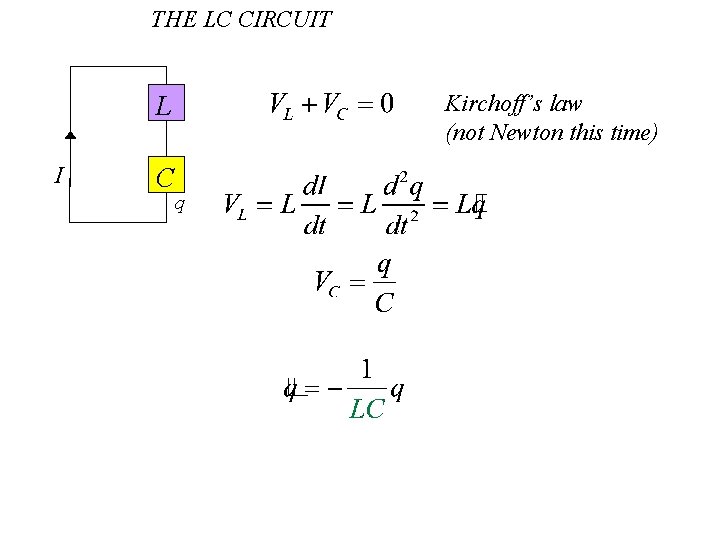
THE LC CIRCUIT DIFFERENTIAL EQUATION L I C q Kirchoff’s law (not Newton this time) Same differential equation as the SHO spring!

What is inductance? ? It is how much magnetic flux is created in the inductor coil by a given current I, in a wire. What is the voltage change across an inductor? A voltage change occurs WHEN there is change in magnetic flux (i. e. some of the energy is ‘converted’ to a magnetic field) 19

THE LC CIRCUIT Kirchoff’s law (not Newton this time) L I C q