Simple Harmonic Motion AP Physics 1 A brief

Simple Harmonic Motion AP Physics 1

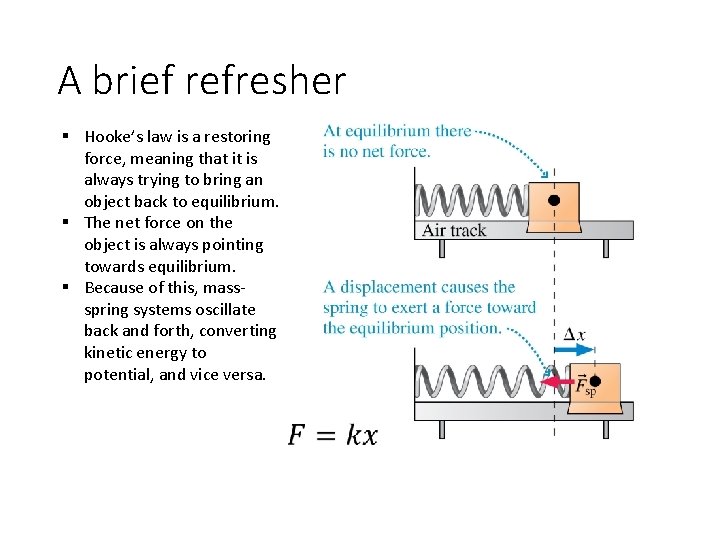
A brief refresher § Hooke’s law is a restoring force, meaning that it is always trying to bring an object back to equilibrium. § The net force on the object is always pointing towards equilibrium. § Because of this, massspring systems oscillate back and forth, converting kinetic energy to potential, and vice versa.

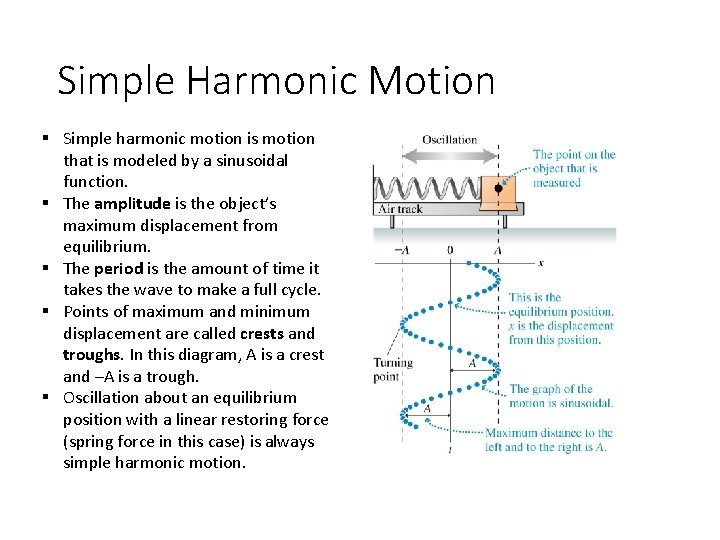
Simple Harmonic Motion § Simple harmonic motion is motion that is modeled by a sinusoidal function. § The amplitude is the object’s maximum displacement from equilibrium. § The period is the amount of time it takes the wave to make a full cycle. § Points of maximum and minimum displacement are called crests and troughs. In this diagram, A is a crest and –A is a trough. § Oscillation about an equilibrium position with a linear restoring force (spring force in this case) is always simple harmonic motion.

Frequency § The period of an oscillator is the amount of time required to complete a full cycle. This is analogous to the period of circular motion, which is the amount of time required to make a full circle. § Frequency is the inverse of period. That means that the frequency is the # of cycles per sec. The commonly used unit is HERTZ (Hz).

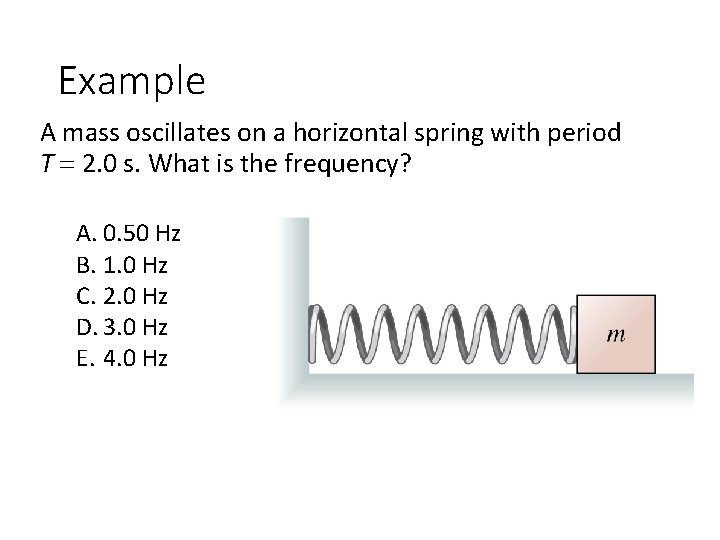
Example A mass oscillates on a horizontal spring with period T 2. 0 s. What is the frequency? A. 0. 50 Hz B. 1. 0 Hz C. 2. 0 Hz D. 3. 0 Hz E. 4. 0 Hz

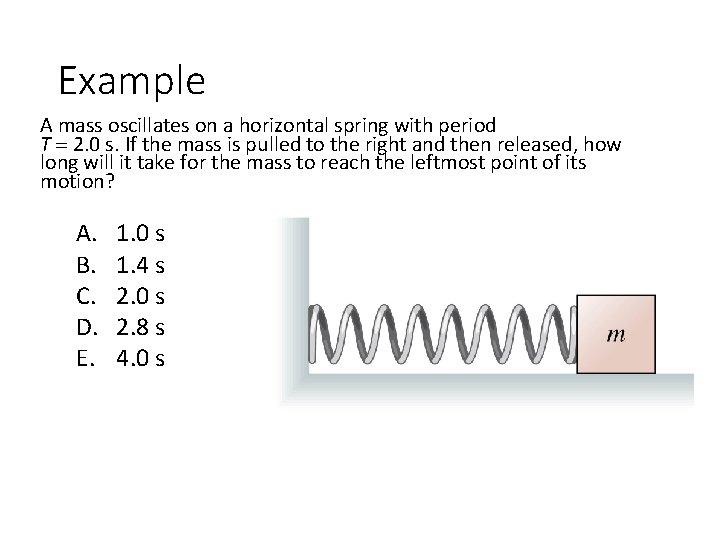
Example A mass oscillates on a horizontal spring with period T 2. 0 s. If the mass is pulled to the right and then released, how long will it take for the mass to reach the leftmost point of its motion? A. B. C. D. E. 1. 0 s 1. 4 s 2. 0 s 2. 8 s 4. 0 s

SHM and Circular Motion § Circular motion and simple harmonic motion are motions that repeat. § Springs behave very similar to objects that move in circles. § The radius of the circle is symbolic of the amplitude of the spring.

Period of a Mass-Spring System § The period of a mass-spring system is given using the following formula: § Notice that the period of a spring is dependent only on the mass attached to it and the spring constant. § This means that the period of the spring is completely independent od the displacement; stretching it further does not change the period of oscillation!

Example A 200 g mass is attached to a spring and executes simple harmonic motion with a period of 0. 25 s If the total energy of the system is 2. 0 J, find the: (a) force constant of the spring 126. 2 N/m (b) the amplitude of the motion 0. 18 m

Pendulums § Pendulums, like springs, oscillate back and forth exhibiting simple harmonic behavior. § The restoring force for a pendulum is one of the components of the gravitational force. Just like with springs, the restoring force is always accelerating the mass back to equilibrium. § The pendulums we will discuss are called simple pendulums, because all of the mass is located at the end. § For a pendulum, the amplitude is measured using angles instead of distances. The angle is measured from equilibrium.

Period of a pendulum § The period of a pendulum is given by the following formula: § Notice that the period does not depend on amplitude or mass of the bob. It only depends on length and the acceleration due to gravity. § Because other planets have different gravitational accelerations, a pendulum on Earth would not have the same period as it does elsewhere in the universe!

Example A visitor to a lighthouse wishes to determine the height of the tower. She ties a spool of thread to a small rock to make a simple pendulum, which she hangs down the center of a spiral staircase of the tower. The period of oscillation is 9. 40 s. What is the height of the tower? 21. 93 m

Modeling SHM § We have said that simple harmonic motion is any motion that can be modeled by a sinusoidal function. This means that we can use either a sine or cosine function in standard form! § We often start making measurements for SHM when an object is at maximum amplitude, so we will use cosine. § A represents our amplitude and f is our frequency. § This allows us to determine where an object is at any point in time as long as we know the amplitude and frequency of the oscillator. § This function works for a mass-spring system, but not for a pendulum. In that case we model angular position as a function of time:

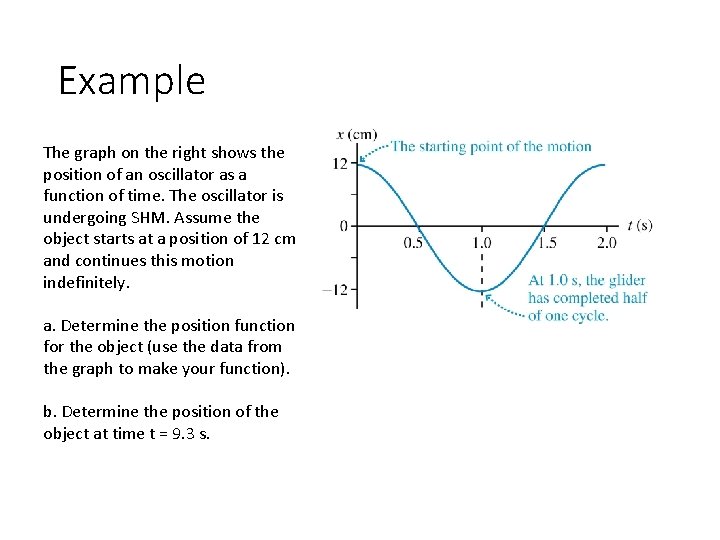
Example The graph on the right shows the position of an oscillator as a function of time. The oscillator is undergoing SHM. Assume the object starts at a position of 12 cm and continues this motion indefinitely. a. Determine the position function for the object (use the data from the graph to make your function). b. Determine the position of the object at time t = 9. 3 s.