Simple Harmonic Motion and Oscillations Oscillations A is

Simple Harmonic Motion and Oscillations

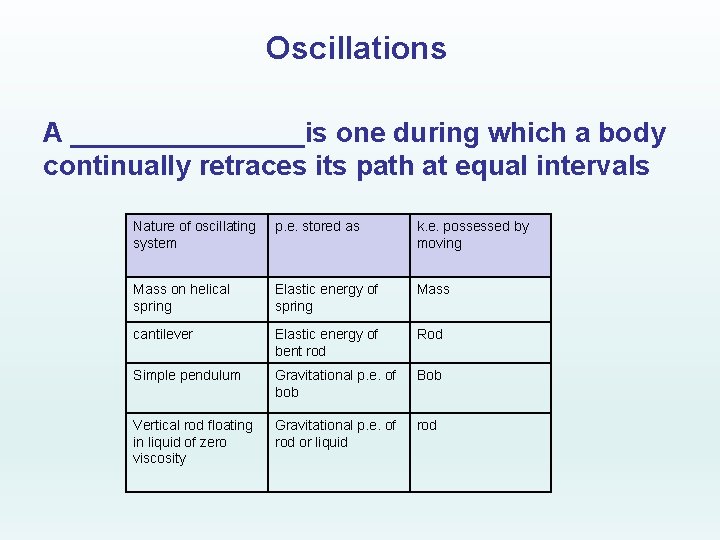
Oscillations A ________is one during which a body continually retraces its path at equal intervals Nature of oscillating system p. e. stored as k. e. possessed by moving Mass on helical spring Elastic energy of spring Mass cantilever Elastic energy of bent rod Rod Simple pendulum Gravitational p. e. of bob Bob Vertical rod floating in liquid of zero viscosity Gravitational p. e. of rod or liquid rod

Oscillations • _______ (x) is the instantaneous distance of the moving object from its mean position (in a specified direction). • A is the _______ of motion: the distance from the centre of motion to either extreme • T is the _______ of motion: the time for one complete cycle of the motion O BP A

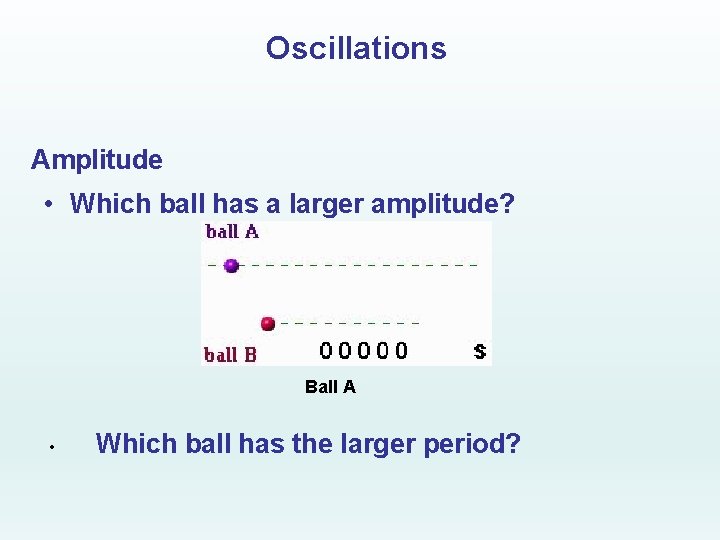
Oscillations Amplitude • Which ball has a larger amplitude? Ball A • Which ball has the larger period?

Oscillations Frequency • The frequency of motion, f, is the rate of repetition of the motion -- the number of cycles per unit time. There is a simple relation between frequency and period: • If ball B has a time period of 12 s, what is the frequency?

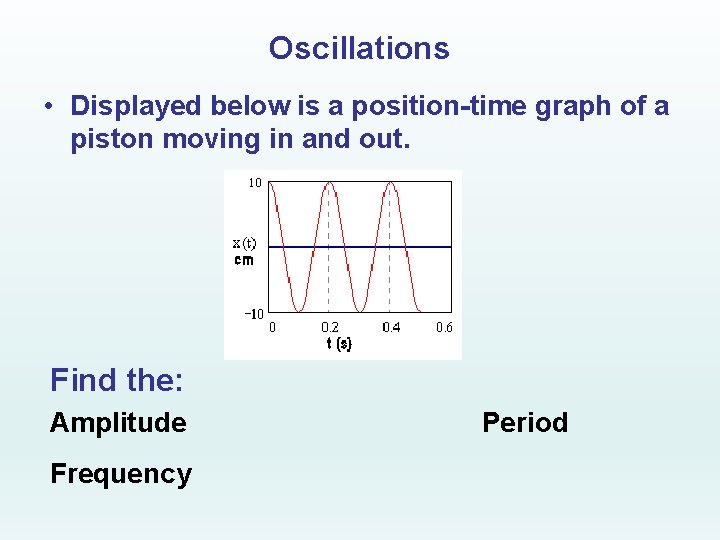
Oscillations • Displayed below is a position-time graph of a piston moving in and out. Find the: Amplitude Frequency Period

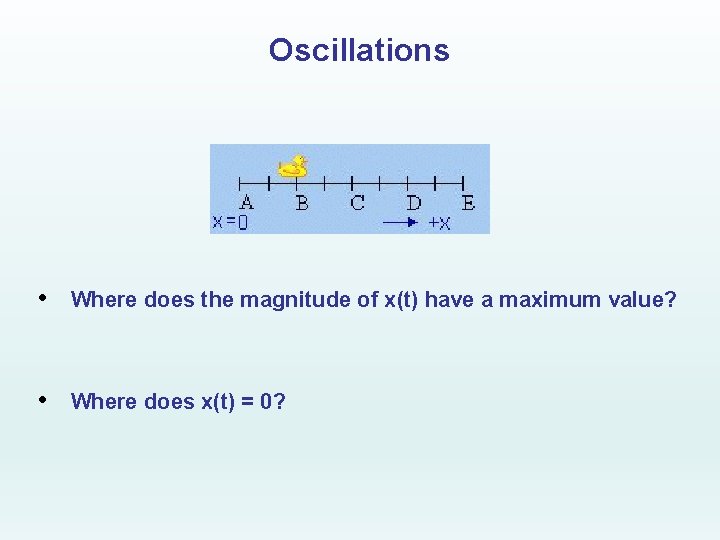
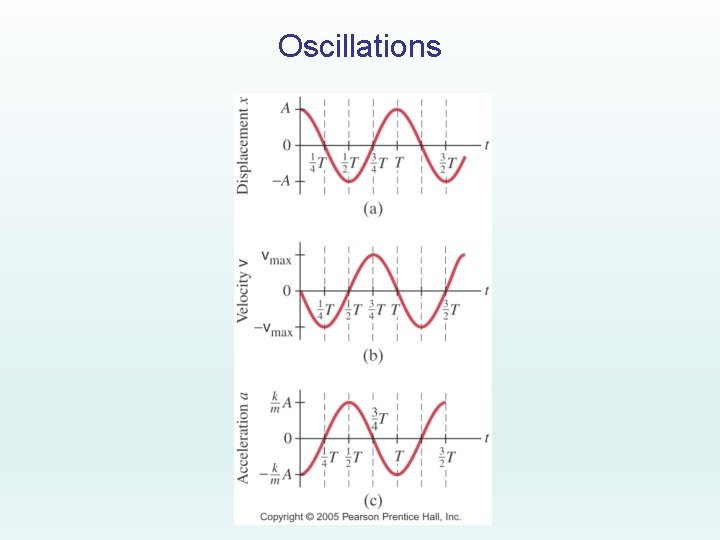
Oscillations • Where does the magnitude of x(t) have a maximum value? • Where does x(t) = 0?

Oscillations • Watch the oscillating duck. Let's consider velocity now • Remember that velocity is a vector, and so has both negative and positive values. • Where does the magnitude of v(t) have a maximum value? • Where does v(t) = 0?

Oscillations • Watch the oscillating duck. Let's consider acceleration now • Remember that acceleration is a vector, and so has both negative and positive values. • Where does the magnitude of a(t) have a maximum value? • Where does a(t) = 0?

Oscillations

Simple Harmonic Motion Any vibrating system where the restoring force is _______ to the negative of the displacement is in simple harmonic motion (SHM), and is often called a simple harmonic oscillator. Three requirements: 1) the acceleration (force) ________to the displacement from the equilibrium position 2) the acceleration (force) is directed _________ the equilibrium position 3) the acceleration (force) is in the _______ direction to the displacement

Simple Harmonic Motion Points to note about Simple Harmonic Motion: • The time period T does _____depend on the amplitude A. • Not all oscillations are simple harmonic motion, but there are many everyday examples of natural simple harmonic motion.

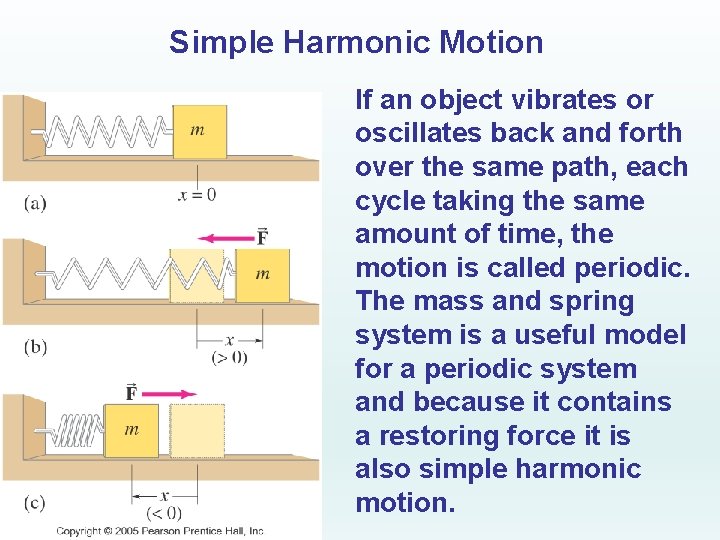
Simple Harmonic Motion If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic. The mass and spring system is a useful model for a periodic system and because it contains a restoring force it is also simple harmonic motion.

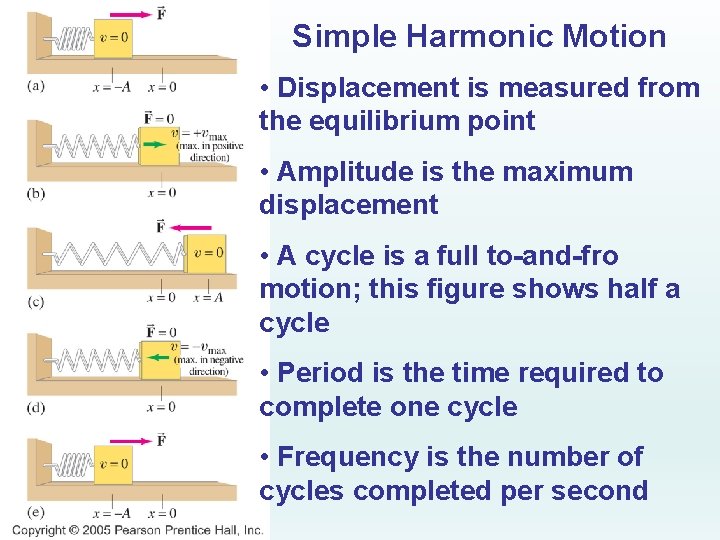
Simple Harmonic Motion • Displacement is measured from the equilibrium point • Amplitude is the maximum displacement • A cycle is a full to-and-fro motion; this figure shows half a cycle • Period is the time required to complete one cycle • Frequency is the number of cycles completed per second

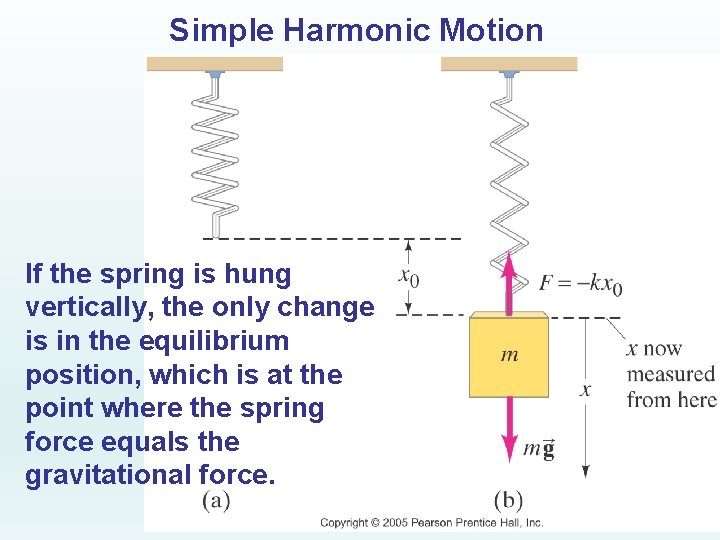
Simple Harmonic Motion If the spring is hung vertically, the only change is in the equilibrium position, which is at the point where the spring force equals the gravitational force.

Simple Harmonic Motion We assume that the surface is frictionless. There is a point where the spring is neither stretched nor compressed; this is the _________position. We measure displacement from that point (x = 0 on the previous figure). The force exerted by the spring depends on the displacement:

Simple Harmonic Motion • The minus sign on the force indicates that it is a restoring force – it is directed to _______the mass to its equilibrium position. • k is the __________ • The force is ______ constant, so the acceleration is ______constant either

Simple Harmonic Motion Simple harmonic motion is defined as the motion that takes place when the acceleration, a, of an object is always directed towards, and proportional to, its displacement from a fixed point. This acceleration is caused by a restoring force that must always be pointed towards the mean position and also proportional to the displacement from the mean position. F -X or F=-(constant) x X Since F=ma a -X or a=-(constant) x X The negative signifies that the acceleration is always pointing back towards the mean position.

Simple Harmonic Motion A graph of the restoring force versus displacement has a slope equal to the________. The stiffer the spring the larger the spring constant will be because more force is required to stretch or compress the spring. A stretched or compressed spring has elastic potential energy. The area underneath a force versus displacement graph is the ____________ stored in the spring or elastic material.

Simple Harmonic Motion The constant of proportionality between acceleration and displacement is often identified as the square of a constant ω which is referred to as the ________________. a=-ω2 x Acceleration a / ms-2 Gradient of line = -ω2 Displacement x / m -A A

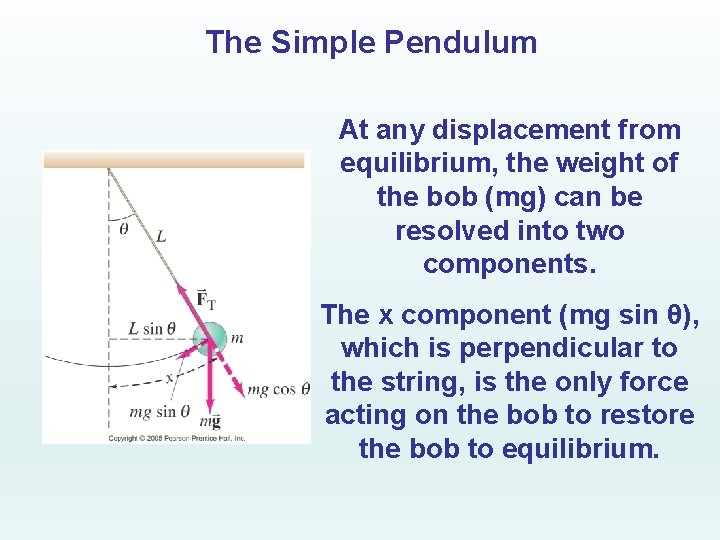
The Simple Pendulum The restoring force of a pendulum is a component of the ______ weight.

The Simple Pendulum At any displacement from equilibrium, the weight of the bob (mg) can be resolved into two components. The x component (mg sin θ), which is perpendicular to the string, is the only force acting on the bob to restore the bob to equilibrium.

The Simple Pendulum The magnitude of the restoring force varies with the bob’s distance from the equilibrium position. The magnitude of the restoring force decreases as the bob moves toward the equilibrium position and becomes zero at the equilibrium position.

The Simple Pendulum At small angles (less than ____), the pendulum’s motion is simple harmonic. When the angle of the displacement is relatively small the restoring force is proportional to the displacement.

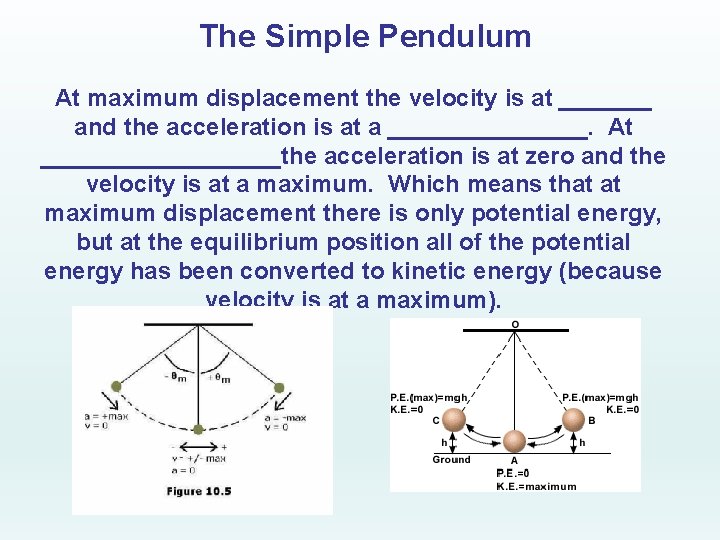
The Simple Pendulum At maximum displacement the velocity is at _______ and the acceleration is at a ________. At _________the acceleration is at zero and the velocity is at a maximum. Which means that at maximum displacement there is only potential energy, but at the equilibrium position all of the potential energy has been converted to kinetic energy (because velocity is at a maximum).

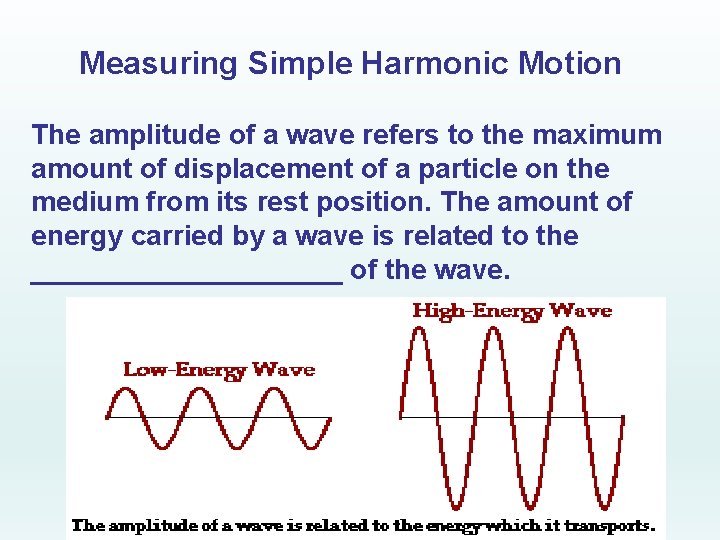
Measuring Simple Harmonic Motion The amplitude of a wave refers to the maximum amount of displacement of a particle on the medium from its rest position. The amount of energy carried by a wave is related to the __________ of the wave.

Measuring Simple Harmonic Motion Period and frequency measure time. Period is the time it takes to execute a complete cycle of motion (time per wave) Frequency is the number of cycles or vibrations per unit time (waves per time) Period and frequency are _______ of one another.

Measuring Simple Harmonic Motion The period of a simple pendulum depends on the pendulum’s ________ and free-fall acceleration. The amplitude (angle) and the mass do _____ affect the period, but the length and gravity do. When the length of the pendulum is increased, the distance the pendulum travels to equilibrium is increased.

Measuring Simple Harmonic Motion The period of a mass-spring system depends on _______ and the ______________: The heavier mass attached to a spring increases inertia without providing a compensating increase in force Because of this increase in inertia, a heavier mass has a smaller acceleration than a lighter mass and therefore takes more time to complete one cycle. Therefore as the mass increases the period increases.

Measuring Simple Harmonic Motion The greater the spring constant (k), the stiffer the spring; hence a greater force is required to stretch or compress the spring. When force is _______, acceleration is greater and the amount of time required for a single cycle would _______.