SIMPLE HARMONIC MOTION A Repeated Type of Motion

SIMPLE HARMONIC MOTION A Repeated Type of Motion

Equilibrium and Oscillation ◦ Equilibrium ◦ NO net force ◦ NO acceleration ◦ Amplitude (A) ◦ The maximum displacement from EQUILIBRIUM ◦ meters ◦ Frequency ◦ The number of cycles / time ◦ Hertz ◦ Period ◦ The time it takes for 1 cycle ◦ Sec.

Linear Restoring Forces and SHM for SPRINGS ◦ If we displace a glider attached to a spring from its equilibrium position, the spring exerts a restoring force back toward equilibrium. ◦ Hook’s Law © 2015 Pearson Education, Inc.

Vertical Mass on a Spring ◦ Draw a FD at a point during oscillation ◦ When is the Equilibrium Pos. Reached (forces) ◦ Fs = F g ◦ Equation ◦ How far a spring will stretch due to its weight

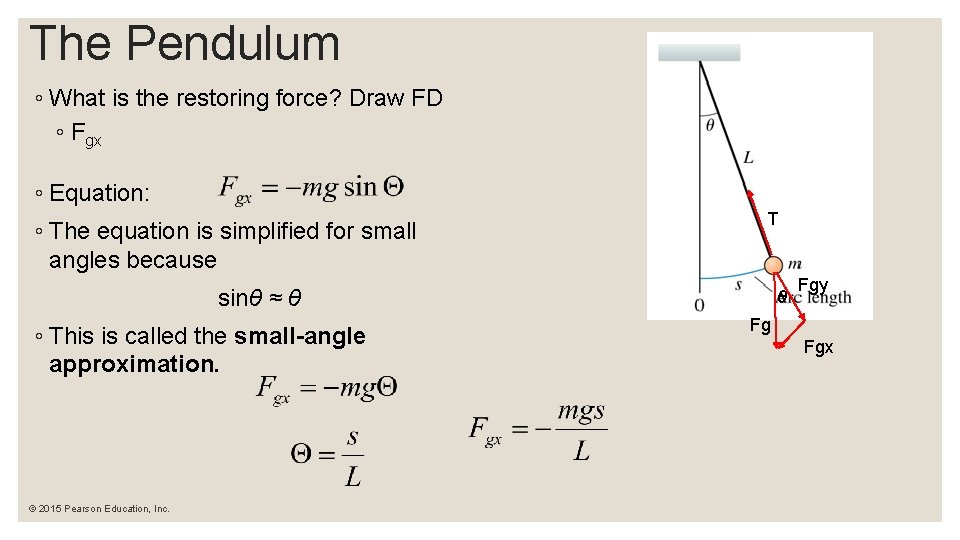
The Pendulum ◦ What is the restoring force? Draw FD ◦ Fgx ◦ Equation: ◦ The equation is simplified for small angles because T sinθ ≈ θ ◦ This is called the small-angle approximation. © 2015 Pearson Education, Inc. θ Fgy Fg Fgx

GIZMO ◦ Periods and frequency and pendulums

Period and Frequency of Springs and Pendulums Spring Pendulum

SHM WKSHT

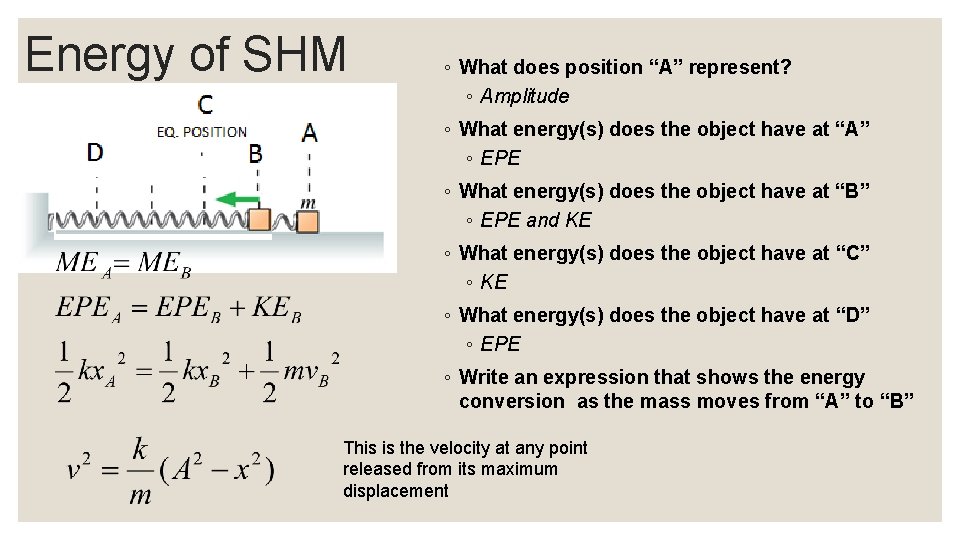
Energy of SHM ◦ What does position “A” represent? ◦ Amplitude ◦ What energy(s) does the object have at “A” ◦ EPE ◦ What energy(s) does the object have at “B” ◦ EPE and KE ◦ What energy(s) does the object have at “C” ◦ KE ◦ What energy(s) does the object have at “D” ◦ EPE ◦ Write an expression that shows the energy conversion as the mass moves from “A” to “B” This is the velocity at any point released from its maximum displacement

Energy of SHM ◦ Where does the mass have its highest velocity? ◦ At “C” ◦ Write an expression using energy for the vmax when the mass is released from “A” ◦ What happens to the energy of the system when you double Amplitude (A)? ◦ It Quadruples ◦ What happens to the vmax when you double Amplitude (A)? ◦ It doubles ◦ What happens to the amax when you double Amplitude (A)? ◦ It doubles

Other Equations of A SPRING in SHM Acceleration Angular Frequency (ω) Magnitude only ∆x = A

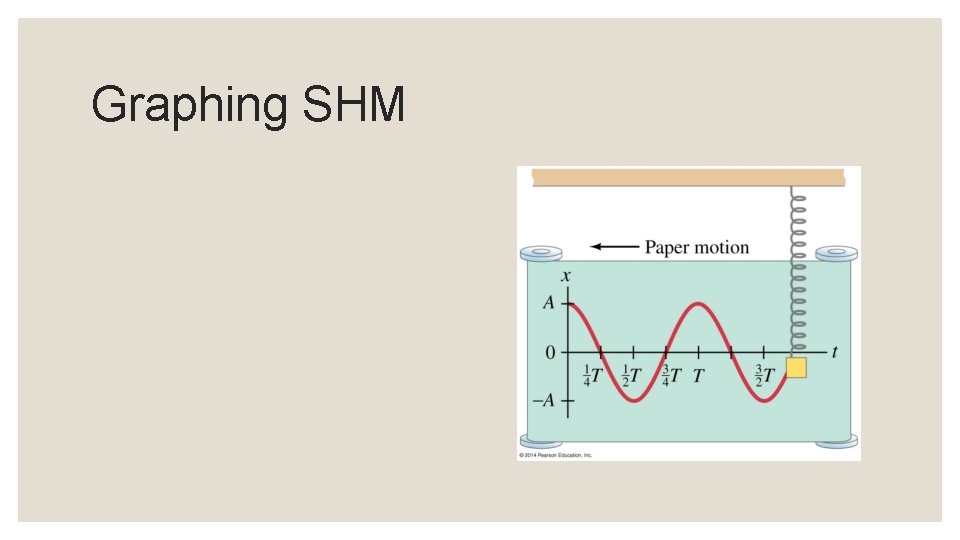
Graphing SHM