Simple CircuitBased SAT Solver Alan Mishchenko 1 Outline

Simple Circuit-Based SAT Solver Alan Mishchenko 1

Outline Ø Motivation Ø Implementation Ø Experiment 2

Motivation for a New SAT Solver Ø Runtime of several applications is dominated by SAT l l Ø SAT sweeping Sequential SAT sweeping (register/signal correspondence) Accumulation of structural choices Computing don’t-cares in a window The problems solved by SAT solver in these applications have the following in common l l l Incremental (each problem has +/- 10 AIG nodes, compared to the previous problem solved) Relatively easy (less than 100 conflicts) Numerous (10 K-100 K problems) 3

Motivation for a Circuit-Based Solver Ø CNF is an intermediate step l Mini. Sat uses more memory to represent CNF, which is not needed for easy problems Ø Circuit is a helpful data-structure l l l It is the primary problem representation It is more compact than CNF It has useful information for the solver Ø Some of these observations are well known in the ATPG community 4

Implementation Ø High-level view of the solver Ø Solver data structures Ø Recursive procedure Ø Additional implementation details 5

High-Level View of the Solver Input: Multi-output combinational AIG Output: SAT solving status for each output SAT: satisfiable (provide a counter-example) UNSAT: unsatisfiable UNDECIDED: the solver’s resource limit is reached status_array Sat. Solver( Sat_Solver * p, Aig_Man * p. Man ) { for each primary output Out of p. Man { if ( Out is driven by a constant ) status = Derive. Status. Simple( Out ); else { PQueue. Assume( p, Driving. Node( Out ) ); status = Sat. Solve_rec( p ); } Add. Status. To. Array( status_array, status ); } return status_array; } 6

Data Structures Ø Constraint data-base (AIG) l Each node is labeled with two binary flags • Assign: Set to 1 iff the node is assigned a value • Value: Set to 1 iff the node’s current value is 1 Ø Propagation queue (PQueue) l Ø The sequence of assignments made Justification queue (JQueue) l The set of nodes to be justified • The output is assigned 0 while inputs are unassigned Ø Node vector containing a SAT assignment l Used to PI nodes participating in a counter-example after a satisfiable SAT run 7

Recursive SAT Procedure status Sat. Solve_rec( Sat_Solver * p ) { if ( PQueue. Propagate( p ) == UNSAT ) return UNSAT; if ( JQueue. Is. Empty( p ) ) return SAT; Aig_Node * Var = JQueue. Select. Variable( p ); int mark = PQueue. Mark. Current. Position( p ); PQueue. Assume( p, !Var ); if ( Sat. Solve_rec( p ) == SAT ) return SAT; PQueue. Cancel. Until( mark ); PQueue. Assume( p, Var ); if ( Sat. Solve_rec( p ) == SAT ) return SAT; return UNSAT; } 8

Implementation Details Ø JQueue is not implemented as an array (as opposed to the traditional implementation as a linked list) l Ø Before each decision JQueue is duplicated and stored away Non-chronological backtracking can be added l Need two additional data-structures • For each assigned node, save its level • For each assigned node, save its reason (NULL, if decision) Ø Recording learned clauses can be added l Ø A learned clause is derived after each conflict Constraint propagation on learned clauses can be added l l Watched literal scheme can be used It is important to keep only learned clauses in the data-base • this allows the solver to derive incomplete assignments 9

Experimental Results (SAT) 10

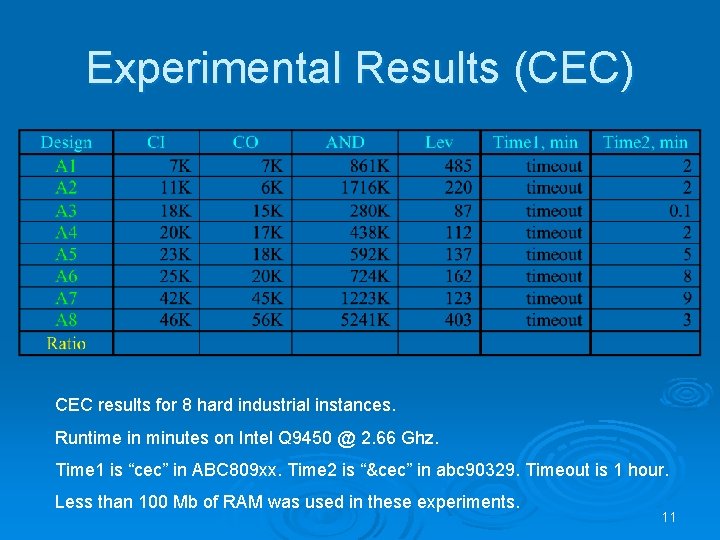
Experimental Results (CEC) CEC results for 8 hard industrial instances. Runtime in minutes on Intel Q 9450 @ 2. 66 Ghz. Time 1 is “cec” in ABC 809 xx. Time 2 is “&cec” in abc 90329. Timeout is 1 hour. Less than 100 Mb of RAM was used in these experiments. 11

Why Mini. SAT Is Slower? Ø Requires multiple intermediate steps l l Window AIG CNF Solving Instead of Window Solving Ø Uses too much memory l l Solver + CNF = 140 bytes / AIG node Instead of 8 -16 bytes / AIG node Ø Decision heuristics l l Are not aware of the circuit structure Instead of Using circuit information 12