SIMILARITY IN TRIANGLES THEOREMS CCGPS STANDARDS MCC 9

SIMILARITY IN TRIANGLES & THEOREMS

CCGPS STANDARDS MCC 9 -12. G. SRT. 2 Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides. MCC 9 -12. G. SRT. 3 Use the properties of similarity transformations to establish the AA criterion for two triangles to be similar.

CCGPS STANDARDS MCC 9 -12. G. SRT. 4 Prove theorems about triangles. Theorems include: a line parallel to one side of a triangle divides the other two proportionally, and conversely; the Pythagorean Theorem proved using triangle similarity. MCC 9 -12. G. SRT. 5 Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures.

ESSENTIAL QUESTION What strategies can I use to determine missing side lengths and areas of similar figures? How do I know which method to use to prove two triangles similar?

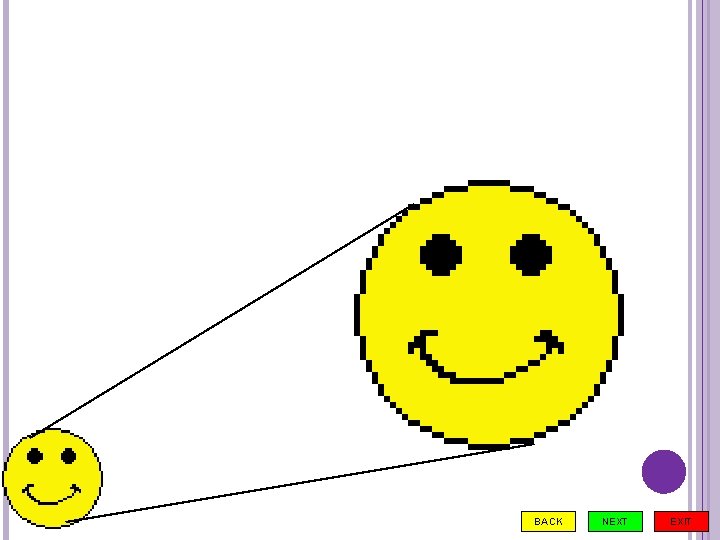
In geometry, two triangles are similar when one is a replica (scale model) of the other. BACK NEXT EXIT

Consider Dr. Evil and Mini Me from Mike Meyers’ hit movie Austin Powers. Mini Me is supposed to be an exact replica of Dr. Evil. BACK NEXT EXIT

BACK NEXT EXIT

How do we know if triangles are similar or proportional? s! id I p Oo w d re? Ho t he ge BACK NEXT EXIT

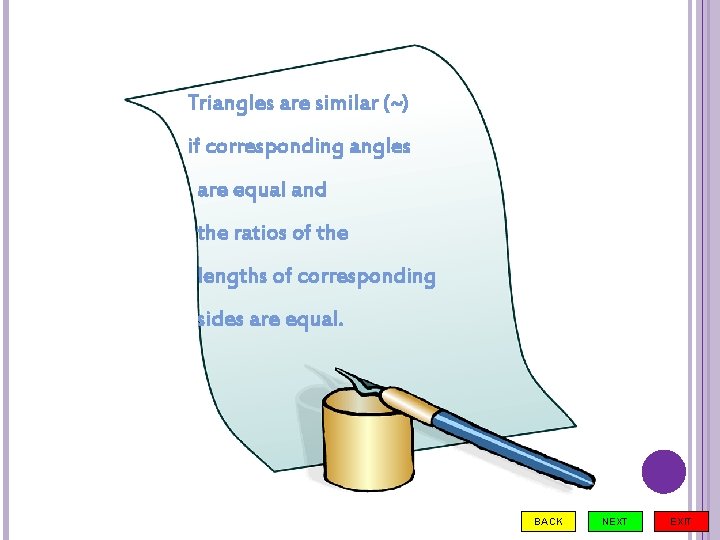
Triangles are similar (~) if corresponding angles are equal and the ratios of the lengths of corresponding sides are equal. BACK NEXT EXIT

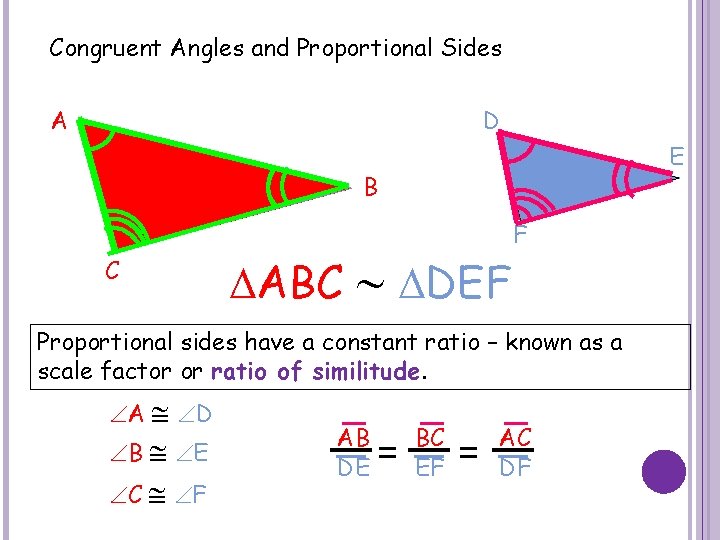
Congruent Angles and Proportional Sides A D E B C ABC DEF F Proportional sides have a constant ratio – known as a scale factor or ratio of similitude. A D B E C F AB BC AC = = DE EF DF

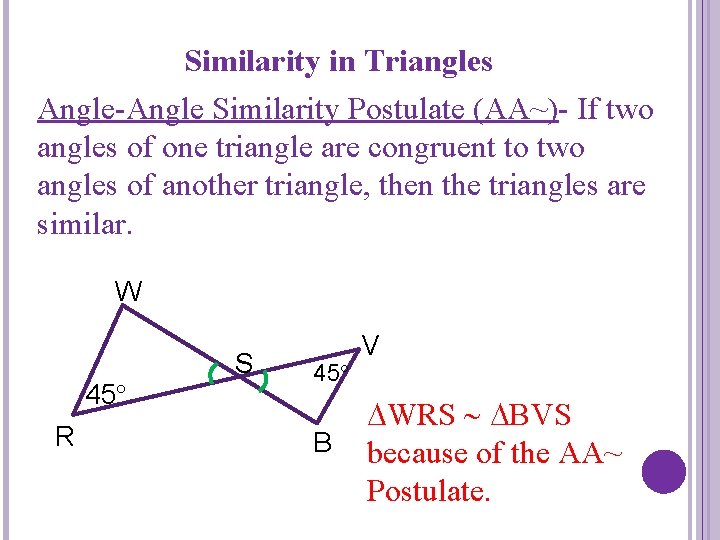
Similarity in Triangles Angle-Angle Similarity Postulate (AA~)- If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. W 45 R S 45 B V WRS BVS because of the AA~ Postulate.

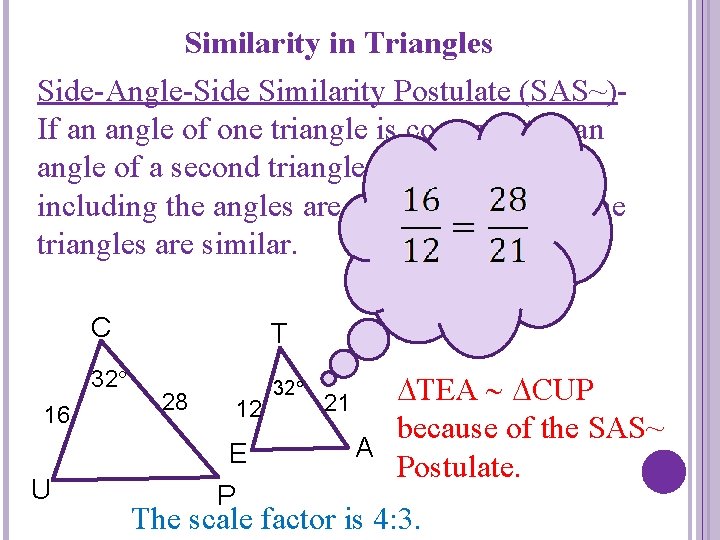
Similarity in Triangles Side-Angle-Side Similarity Postulate (SAS~)If an angle of one triangle is congruent to an angle of a second triangle, and the sides including the angles are proportional, then the triangles are similar. 16 C T 32 28 12 E U P 21 TEA CUP because of the SAS~ A Postulate. The scale factor is 4: 3.

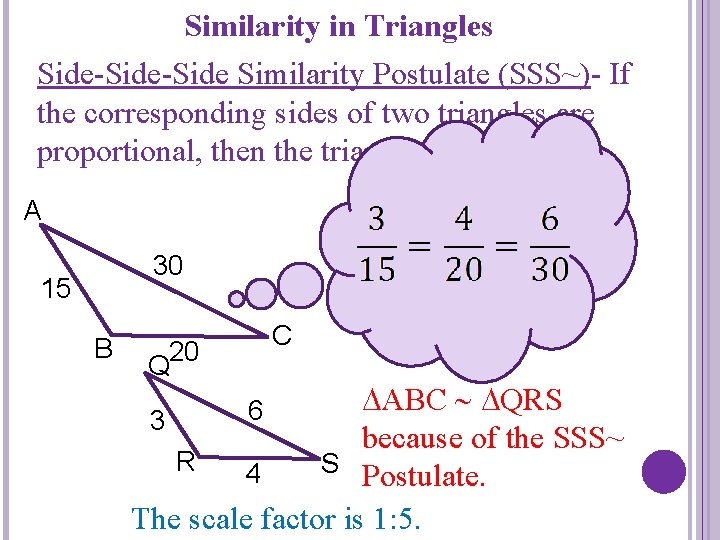
Similarity in Triangles Side-Side Similarity Postulate (SSS~)- If the corresponding sides of two triangles are proportional, then the triangles are similar. A 30 15 B C Q 20 ABC QRS 3 because of the SSS~ R S Postulate. 4 The scale factor is 1: 5. 6

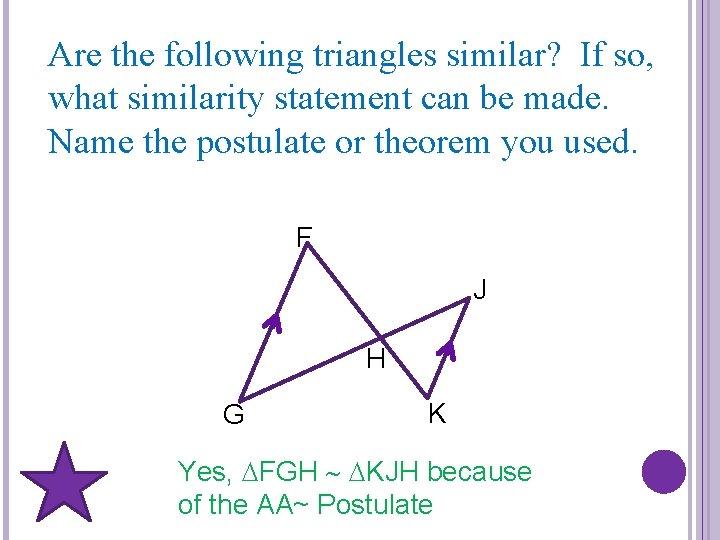
Are the following triangles similar? If so, what similarity statement can be made. Name the postulate or theorem you used. F J H G K Yes, FGH KJH because of the AA~ Postulate

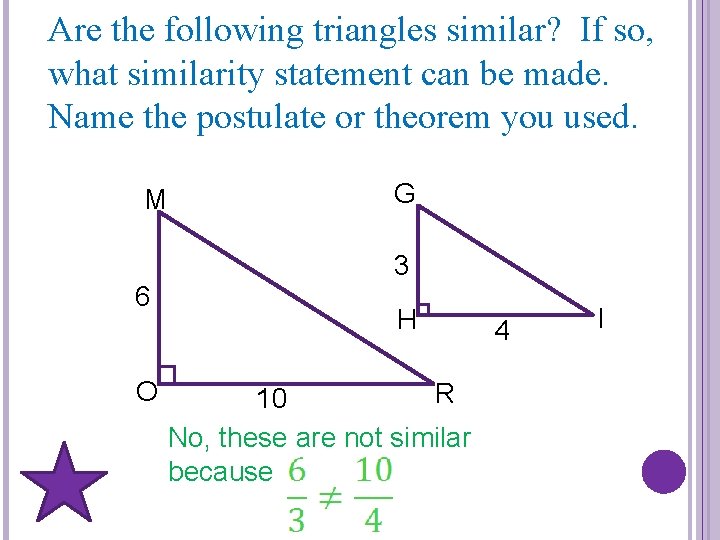
Are the following triangles similar? If so, what similarity statement can be made. Name the postulate or theorem you used. M 6 O G 3 H R 10 No, these are not similar because 4 I

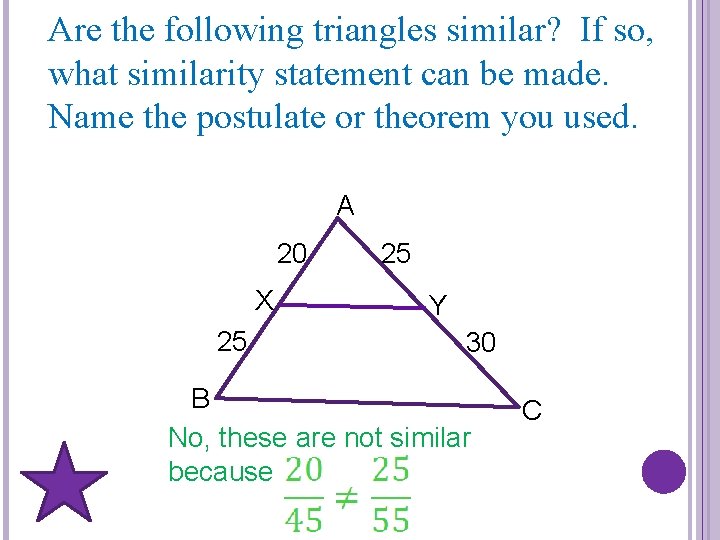
Are the following triangles similar? If so, what similarity statement can be made. Name the postulate or theorem you used. A 20 X 25 25 Y 30 B No, these are not similar because C

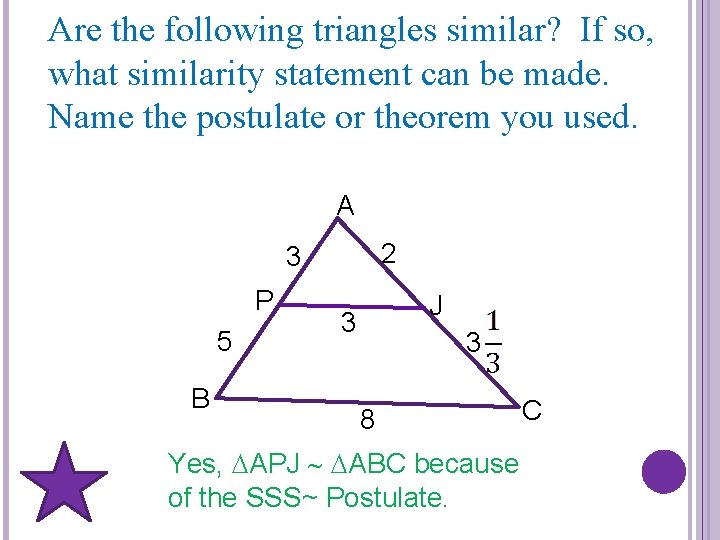
Are the following triangles similar? If so, what similarity statement can be made. Name the postulate or theorem you used. A 2 3 P 5 B J 3 3 8 C Yes, APJ ABC because of the SSS~ Postulate.

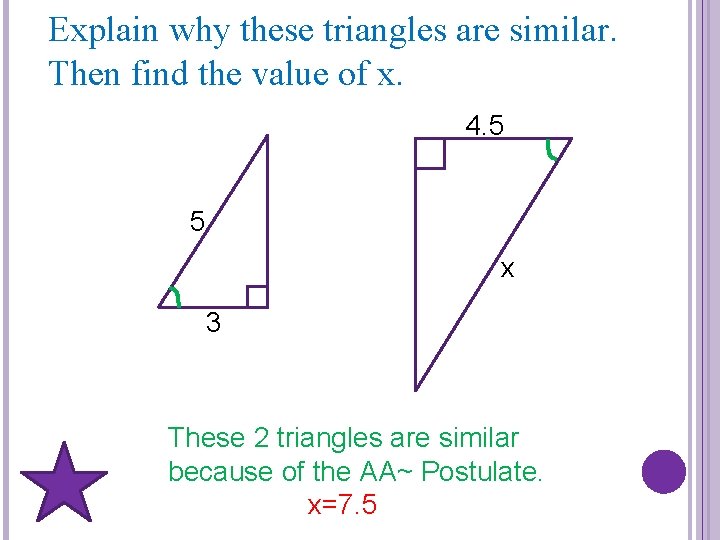
Explain why these triangles are similar. Then find the value of x. 4. 5 5 x 3 These 2 triangles are similar because of the AA~ Postulate. x=7. 5

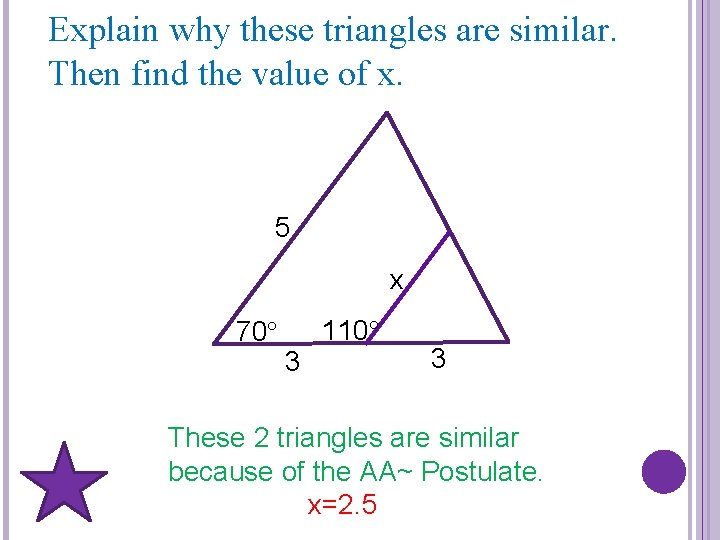
Explain why these triangles are similar. Then find the value of x. 5 x 70 3 110 3 These 2 triangles are similar because of the AA~ Postulate. x=2. 5

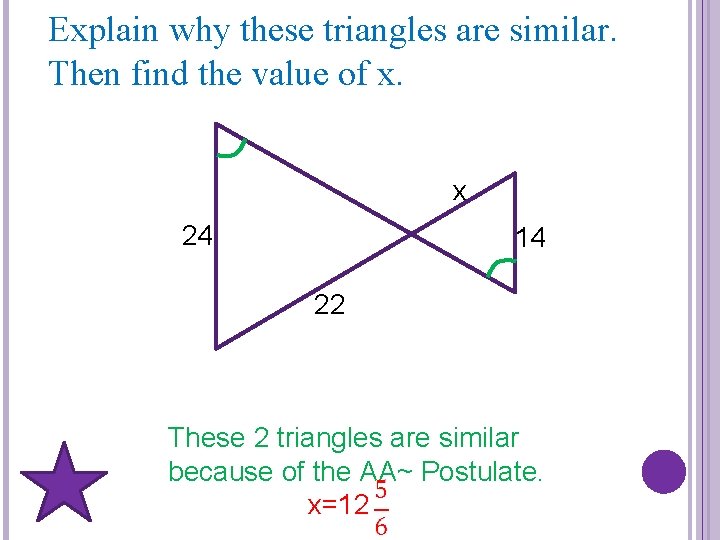
Explain why these triangles are similar. Then find the value of x. x 24 14 22 These 2 triangles are similar because of the AA~ Postulate. x=12

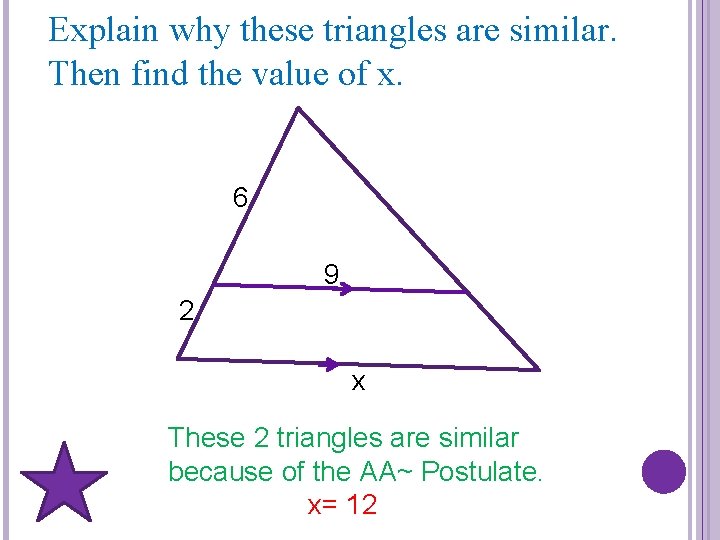
Explain why these triangles are similar. Then find the value of x. 6 9 2 x These 2 triangles are similar because of the AA~ Postulate. x= 12

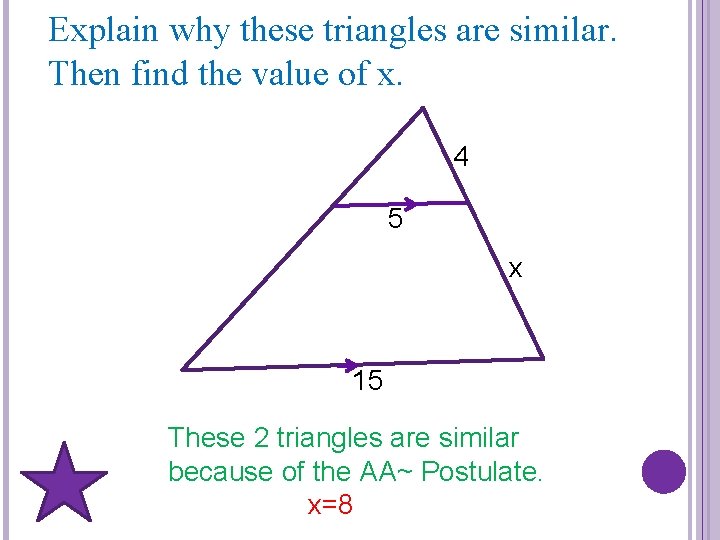
Explain why these triangles are similar. Then find the value of x. 4 5 x 15 These 2 triangles are similar because of the AA~ Postulate. x=8

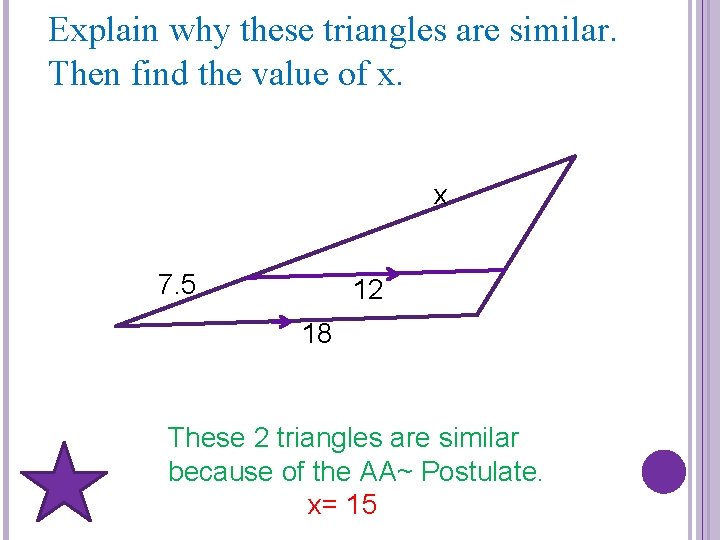
Explain why these triangles are similar. Then find the value of x. x 7. 5 12 18 These 2 triangles are similar because of the AA~ Postulate. x= 15

Please complete the Ways to Prove Triangles Similar Worksheet.

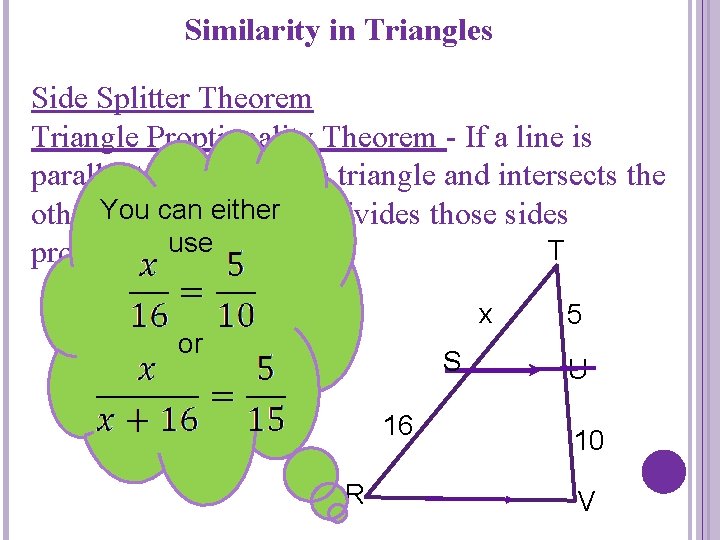
Similarity in Triangles Side Splitter Theorem Triangle Proptionality Theorem - If a line is parallel to one side of a triangle and intersects the other You can either two sides, then it divides those sides use T proportionally. x or S 16 R 5 U 10 V

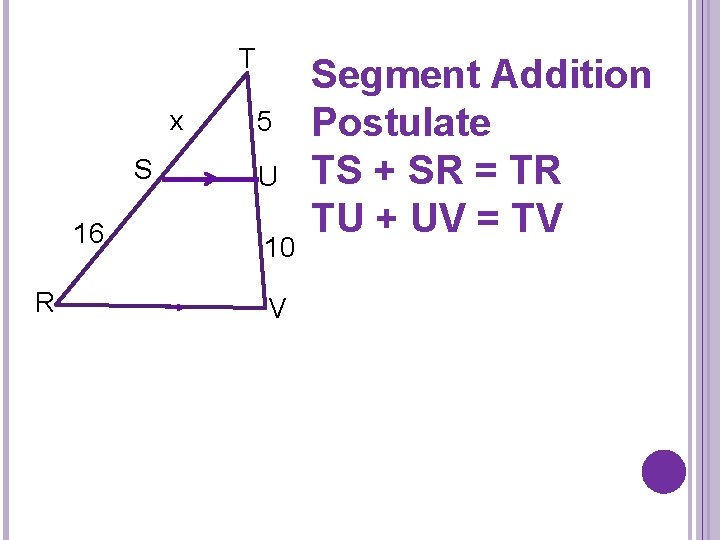
T x S 16 R 5 U 10 V Segment Addition Postulate TS + SR = TR TU + UV = TV

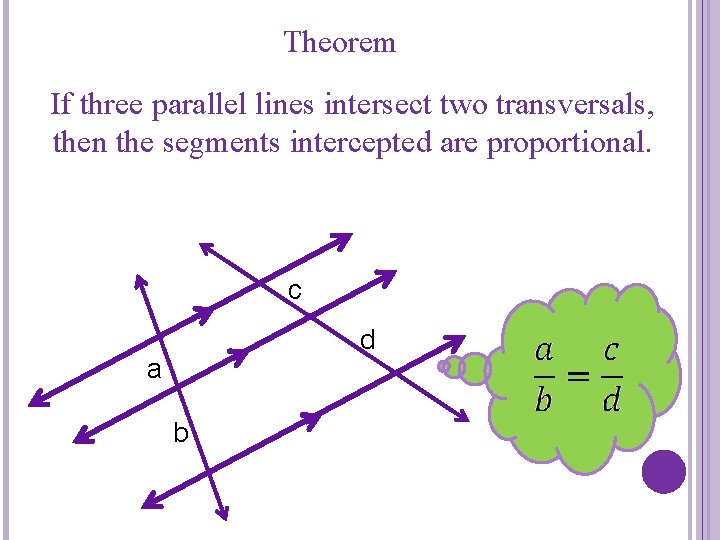
Theorem If three parallel lines intersect two transversals, then the segments intercepted are proportional. c d a b

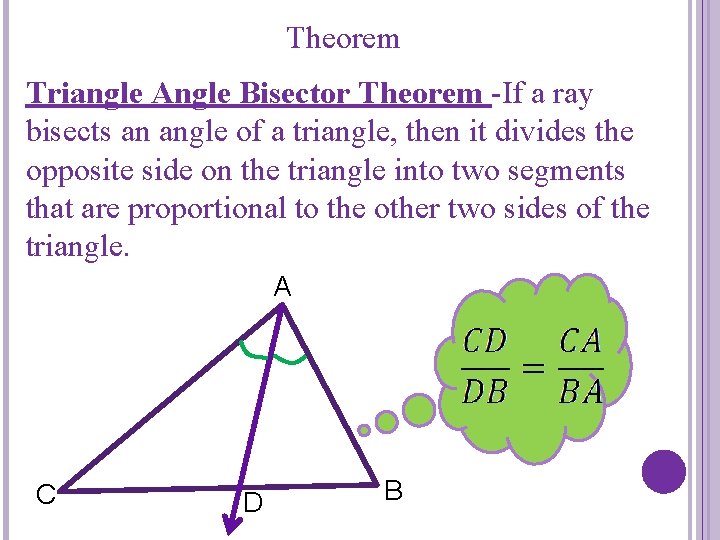
Theorem Triangle Angle Bisector Theorem -If a ray bisects an angle of a triangle, then it divides the opposite side on the triangle into two segments that are proportional to the other two sides of the triangle. A C D B

Complete the practice sheets.